深度学习入门（九） 多层感知机实现

前言

核心内容来自博客链接1博客连接2希望大家多多支持作者
本文记录用，防止遗忘

多层感知机从零实现

为了与之前softmax回归，获得的结果进行比较， 我们将继续使用Fashion-MNIST图像分类数据集

1 获取和读取数据

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
1
2
3
4
5
6
7

2 初始化模型参数

回想一下，Fashion-MNIST中的每个图像由28×28=784个灰度像素值组成。 所有图像共分为10个类别。 忽略像素之间的空间结构， 我们可以将每个图像视为具有784个输入特征 和10个类的简单分类数据集。 首先，我们将实现一个具有单隐藏层的多层感知机， 它包含256个隐藏单元。 注意，我们可以将这两个变量都视为超参数。 通常，我们选择2的若干次幂作为层的宽度。 因为内存在硬件中的分配和寻址方式，这么做往往可以在计算上更高效。

我们用几个张量来表示我们的参数。 注意，对于每一层我们都要记录一个权重矩阵和一个偏置向量。 跟以前一样，我们要为损失关于这些参数的梯度分配内存。

# 输入个数，输出个数，隐藏层的个数（超参数）
num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = torch.randn(num_inputs, num_hiddens, requires_grad=False)
W1 = W1 * 0.01
W1.requires_grad=True
b1 = torch.zeros(num_hiddens, requires_grad=True)
W2 = torch.randn(num_hiddens,num_outputs,requires_grad=False)
W2 = W2 * 0.01
W2.requires_grad=True
b2 = torch.zeros(num_outputs,requires_grad=True)

params = [W1,b1,W2,b2]
1
2
3
4
5
6
7
8
9
10
11
12
13

我们在（softmax回归的从零开始实现）里已经介绍了，Fashion-MNIST数据集中图像形状为 28×28，类别数为10。本节中我们依然使用长度为 28×28=784 的向量表示每一张图像。因此，输入个数为784，输出个数为10。实验中，我们设超参数隐藏单元个数为256。

num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_hiddens)), dtype=torch.float)
b1 = torch.zeros(num_hiddens, dtype=torch.float)
W2 = torch.tensor(np.random.normal(0, 0.01, (num_hiddens, num_outputs)), dtype=torch.float)
b2 = torch.zeros(num_outputs, dtype=torch.float)

params = [W1, b1, W2, b2]
for param in params:
    param.requires_grad_(requires_grad=True)

1
2
3
4
5
6
7
8
9
10
11

3 激活函数

为了确保我们对模型的细节了如指掌， 我们将实现ReLU激活函数， 而不是直接调用内置的relu函数。

def relu(X):
  a = torch.zeros_like(X)
  return torch.max(X,a)
1
2
3

4 模型

因为我们忽略了空间结构， 所以我们使用reshape将每个二维图像转换为一个长度为num_inputs的向量。 只需几行代码就可以实现我们的模型。

  # 将图片拉成一个矩阵784长度
  X = X.reshape((-1,num_inputs))
  H = relu(X @ W1 + b1)
  return (H @ W2 + b2)
1
2
3
4

5 损失函数

# 4 损失函数
# loss = nn.CrossEntropyLoss()
loss = nn.CrossEntropyLoss(reduction='none')
# reduction='none'加上这个图例才会出现train loss蓝线，不知道为啥
1
2
3
4

6 训练

幸运的是，多层感知机的训练过程与softmax回归的训练过程完全相同。 可以直接调用d2l包的train_ch3函数，实现可见前面内容

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
# loss不出来说明loss太大超过0.8了
1
2
3
4

注：由于原书的mxnet中的SoftmaxCrossEntropyLoss在反向传播的时候相对于沿batch维求和了，而PyTorch默认的是求平均，所以用PyTorch计算得到的loss比mxnet小很多（大概是maxnet计算得到的1/batch_size这个量级），所以反向传播得到的梯度也小很多，所以为了得到差不多的学习效果，我们把学习率调得成原书的约batch_size倍，原书的学习率为0.5，这里设置成100.0。(之所以这么大，应该是因为d2lzh_pytorch里面的sgd函数在更新的时候除以了batch_size，其实PyTorch在计算loss的时候已经除过一次了，sgd这里应该不用除了)

7 预测

# 6 预测
d2l.predict_ch3(net,test_iter)
1
2

输出

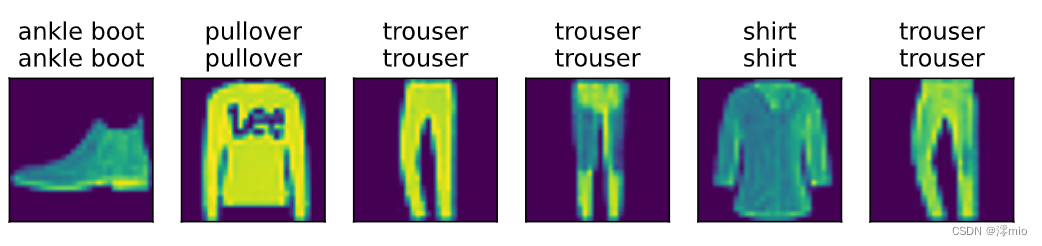
多层感知机简洁实现

import torch
from torch import nn
from d2l import torch as d2l
1
2
3

net = nn.Sequential(nn.Flatten(),# 将图片矩阵转换成一个向量
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);
1
2
3
4
5
6
7
8
9
10

batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
1
2
3
4
5
6

输出：

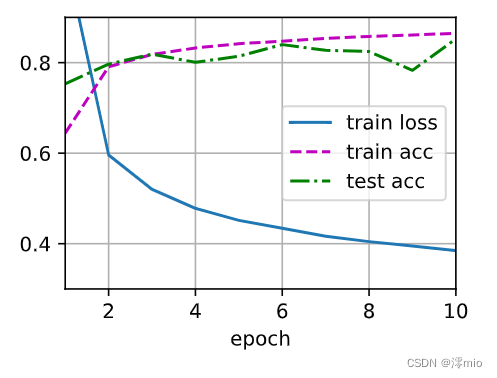
小结

可以通过手动定义模型及其参数来实现简单的多层感知机。
当多层感知机的层数较多时，本节的实现方法会显得较烦琐，例如在定义模型参数的时候。