• Chapter 10 聚类

    1 相似度度量的方法与相互联系

    1.1 方法

    闵可夫斯基Minkowski/欧式距离 dist(X,Y)=(\sum _{i=1}^{n} |x_{i}-y_{i}|^{p})^{\frac{1}{p}}

    杰卡德相似系数（Jaccard）J(A,B)=\frac{|A\bigcap B|}{|A\bigcup B|}

    余弦相似度cos(\theta )=\frac{a^{T}b}{|a|\cdot |b|}

    Pearson相似系数\rho _{XY}=\frac{cov(X,Y)}{\sigma _{X}\sigma _{Y}}=\frac{E[(X-\mu _{X})(Y-\mu _{Y})]}{\sigma _{X}\sigma _{Y}}=\frac{\sum _{i=1}^{n}(X_{i}-\mu _{X})(Y_{i}-\mu _{Y})}{\sqrt{\sum _{i=1}^{n}(X_{i}-\mu _{X})^{2}}\sqrt{\sum _{i=1}^{n}(Y_{i}-\mu _{Y})^{2}}}

    相对熵（K-L距离）D(p||q)=\sum _{x}p(x)log\frac{p(x)}{q(x)}=E_{p(x)}\frac{p(x)}{q(x)}

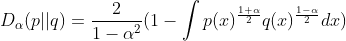
    Hellinger距离D_{\alpha }(p||q)=\frac{2}{1-\alpha ^{2}}(1-\int p(x)^{\frac{1+\alpha }{2}}q(x)^{\frac{1-\alpha }{2}}dx)

    ps:假设(x_{1}-x_{2})最大，则\underset{p\rightarrow \infty }{lim}[(x_{1}-x_{2})^{p}+(y_{1}-y_{2})^{p}+(z_{1}-z_{2})^{p}]^{\frac{1}{p}}=\underset{p\rightarrow \infty }{lim}[(x_{1}-x_{2})(1+(\frac{(y_{1}-y_{2})}{(x_{1}-x_{2})})^{p}+(\frac{(z_{1}-z_{2})}{(x_{1}-x_{2})})^{p}]^{\frac{1}{p}}=(x_{1}-x_{2})

    1.2 相互联系

    余弦相似度与Pearson相似系数之间的关系：

    n维向量x和y的夹角记做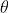\theta，根据余弦定理，其余弦值为：cos(\theta )=\frac{x^{T}y}{|x|\cdot |y|}=\frac{\sum_{i=1}^{n}x_{i}y_{i}}{\sqrt{\sum_{i=1}^{n}x_{i}^{2}}\sqrt{\sum_{i=1}^{n}y_{i}^{2}}}

    这两个向量的相关系数是：

    \rho _{XY}=\frac{cov(X,Y)}{\sigma _{X}\sigma _{Y}}=\frac{E[(X-\mu _{X})(Y-\mu _{X})]}{\sigma _{X}\sigma _{Y}}=\frac{\sum_{i=1}^{n}(x_{i}-\mu_{X} )(y_{i}-\mu _{Y})}{​{\sqrt{\sum _{i=1}^{n}(X_{i}-\mu _{X})^{2}}\sqrt{\sum _{i=1}^{n}(Y_{i}-\mu _{Y})^{2}}} }

    相关系数就是将x,y坐标向量各自平移到原点后的夹角余弦。

    2 K-means聚类的思路和使用条件

    2.1 定义

    聚类就是对大量未知标注的数据集，按数据的内在相似性将数据集划分为多个类别，使类别内的数据相似度较大而类别间的数据相似度较小。是一种无监督学习。

    2.2 思路

    基本思想：对于给定的类别数目k，首先给出初始划分，通过迭代改变样本和簇的隶属关系，使得每一次改进之后的划分方案都较前一次好。

    2.3 使用条件

    给定一个有N个对象的数据集，构造数据的k个簇，k\leq n。满足下列条件：
    （1）每一个簇至少包含一个对象

    （2）每一个对象属于且仅属于一个簇

    （3）将满足上述条件的k个簇称作一个合理划分 

    2.4 算法

    •  k-Means将簇中所有点的均值作为新质心，但是若簇中含有异常点，会将导致均值偏离严重。因此，这时将簇中所有点的中位数作为新质心更为稳妥，这种聚类方式叫做k-Mediods聚类。
    • 初值的选择是人为选择。

    2.5 k-means的公式化解释

    2.6 聚类的衡量指标

    •  均一性：一个簇只包含一个类别的样本，则满足均一性。

    • 完整性：同类别样本被归类到相同簇中，则满足完整性。

    • PS:均一性和完整性相反，若均一性好则完整性就不太好；若完整性好则均一性就不太好。

    2.7 k-means聚类方法的总结

    优点：

    • 是解决聚类问题的一种经典算法，简单、快速
    • 对处理大数据集，该算法保持可伸缩性和高效率
    • 当簇近似为高斯分布时，它的效果较好

    缺点：

    • 在簇的平均值可被定义的情况下才能使用，可能不适用于某些应用
    • 必须事先给出k(要生成的簇的数目)，而且对初值敏感，对于不同的初始值，可能会导致不同结果。
    • 不适合于发现非凸形状的簇或者大小差别很大的簇
    • 对躁声和孤立点数据敏感

    可作为其他聚类方法的基础算法，如谱聚类

    2.8 聚类模型

    (1) ARI：

    数据集S共有N个元素，两个聚类结果分别是：X=\left \{ X_{1},X_{2},...,X_{r} \right \},Y=\left \{ Y_{1},Y_{2},...,Y_{s} \right \}

    X和Y的元素个数为：a=\left \{ a_{1},a_{2},...,a_{r} \right \},b=\left \{ b_{1},b_{2},...,b_{s} \right \}

    记：n_{ij}=|X_{i}\bigcap Y_{i}|

    则：ARI=\frac{Index-EIndex}{MaxIndex-EIndex}=\frac{\sum_{i,j}C_{n_{ij}}^{2}-\frac{[\sum_{i}C_{b_{j}}^{2}\cdot \sum_{j}C_{b_{j}}^{2}]}{C_{n}^{2}}}{\frac{1}{2}\frac{[\sum_{i}C_{a_{i}}^{2}+\sum_{j}C_{b_{j}}^{2}]-[\sum_{i}C_{b_{j}}^{2}\cdot \sum_{j}C_{b_{j}}^{2}]}{C_{n}^{2}}}

    (2) AMI

    根据信息熵得到互信息/正则化信息：

    MI(X,Y)=\sum_{i=1}^{r}\sum_{j=1}^{s}P(i,j)log\frac{p(i,j)}{P(i)P(j)}

    NMI(X,Y)=\frac{MI(X,Y)}{\sqrt{H(X)H(Y)}}

    X服从超几何分布，求的互信息的期望为：

    E(MI) = \sum_{x} ^{} P(X=x) MI(X,Y) = \sum_{x=max(1,a_{i}+b_{i}-N)}^{min(a_{i},b_{i})}[MI\cdot \frac{a_{i}!b_{j}!(N-a_{i})!(N-b_{j})!}{N!x!(a_{i}-x)!(b_{j}-x)!(N-a_{i}-b_{j}+x)!}]

    从而有：AMI(X,Y)=\frac{MI(X,Y)-E[MI(X,Y)]}{max\left \{ H(X),H(Y) \right \}-E[MI(X,Y)]}

    2.9 轮廓系数

     

    3 层次聚类的思路和方法

    3.1 思路

    层次聚类方法对给定的数据集进行层次的分解，直到某种条件满足为止。

    分两种：

    （1）凝聚的层次聚类：AGNES算法——一种自底向上的策略。首先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到某个终结条件被满足。

    （2）分裂的层次聚类：DIANA算法——采用自顶向下的策略。首先将所有对象置于一个簇中，然后逐渐细分为越来越小的簇，直到达到了某个终结条件。

    3.2 算法

    4 密度聚类

    4.1 介绍

    指导思想——只要样本点的密度大于某阈值，则将该样本添加到最近的簇中。

    优点——能克服基于距离的算法只能发现“类圆形”（凸）的聚类的缺点，可发现任意形状的聚类，且对噪声数据不敏感。但计算密度单元的计算复杂度更大，需要建立空间索引来降低计算量。

    4.2 密度聚类模型

    DBSCAN算法

     

     

     

    密度最大值聚类

     

    5  复习特征值

    （1）实对称阵的特征值是实数

    （2） 实对称阵不同特征值的特征向量正交

    6 谱和谱聚类 

    方阵作为线性算子，它的所有特征值的全体统称方阵的谱。

    • 方阵的谱半径为最大的特征值
    • 矩阵A的谱半径：（A^{T}A）的最大特征值

    谱聚类是一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类，从而达到对样本数据聚类的目的。

    样本形成的矩阵W=(w_{ij})， 取第i行的权值相加作为di，即第i样本的度，组成矩阵D。求L前k小的特征值对应的特征向量所形成的u矩阵，对它做k均值，就得到了普聚类的最终结果。

    6.1 拉普拉斯

    6.2  谱聚类算法

    • 未正则拉普拉斯矩阵

    •  随机游走拉普拉斯矩阵
    •  对称拉普拉斯矩阵

  • 相关阅读:
    export ‘OrbitControls‘ was not found in ‘three‘
    docker安装mongodb
    管理与系统思维
    关于 Node.js 参数 max-old-space-size
    Arthas使用总结
    【C++】引用
    散列表查找技术（数据结构）
    相关回归常见问题
    ES6总结
    jasperreports6.12.2 could not load the following font解决方法
  • 原文地址：https://blog.csdn.net/qwertyuiop0208/article/details/126083526