第一章 矩阵与线性方程组（十）

1.正态随机向量

• 若随机向量 $x(\xi )=[x_1(\xi ),x_2(\xi ),\dots ,x_m(\xi ){]}^T$的各分量为联合正态分布的随机变量，则称$x(\xi )$为正态随机向量。实随机向量和复随机向量的概率密度函数表示稍有不同。
• 一个均值向量为${\mu }_x$和协方差矩阵为${Г}_x$的实正态随机向量记作$xN(u_x,{Г}_x$，其概率密度函数为
  
  式中，$|{Г}_x|$表示矩阵的行列式，指数项$(x-u_x{)}^T{Г}_x^{-1}(x-{\mu }_x)$是$x_i$的正定二次型函数，也可以写作
  
  式中，${Г}_x^{-1}=(i,j)$表示逆矩阵${Г}_x^{-1}$的$(i,j)$元素，$u_i$=$E{x}_i$是随机变量$x_i$的均值。
  实正态随机向量的特征函数为
  
  式中，$w=[w_1，w_2,\dots ,w_m{]}^T$。
• 令$x=[x_1,x_2,\dots ，x_m{]}^T$，其每个元素服从复正态分布，即$x_{i}CN({\mu }_i，{\sigma }_i^2)$，则$x$称为复正态随机向量，记作$xCN({\mu }_x，{Г}_x)$，其中，$\mu =[{\mu }_1,{\mu }_2,\dots {\mu }_m{]}^T$。若$x_i=u_i+j{v}_i$,并且实随机向量$[u_1,v_1{]}^T,[u_2,v_2{]}^T,\dots ,[u_m,v_m{]}^T$统计独立，则复随机正态向量$x$的概率密度函数为
  
  式中，${Г}_x=diag({\sigma }_1^2,{\sigma }_2^2,\cdot \cdot \cdot ,{\sigma }_m^2)$。复正态随机向量的特征函数由下式给出:
  

2.正态随机向量的重要性质。

(1)概率密度函数由均值向量和协方差矩阵完全描述。
(2)若正态随机向量的各个分量相互统计不相关，则它们也是统计独立的。
(3)均值向量$u_x$和协方差矩阵${Г}_x$的正态随机向量$x$的线性变换$y(\xi )=Ax(\xi )$仍然为正态随机向量，其概率密度函数为

3.举例

以信号处理中的加性噪声作为典型例子，说明实正态随机向量与复正态随机向量的统计表示的不同。
在阵列处理、无线通信和多信道信号处理中，常常使用多个传感器或者陈元接收多路信号。在大多数情况下，可以假定每个传感器上的加性噪声都是高斯白噪声，并且这些传感器上的加性高斯白噪声是彼此统计不相关的。

• 例：令$x(t)=|x_1(t),x_2(t),\dots ,x_m(t){]}^T$为一实值正态随机向量，其中，$x_1(t),x_2(t),\dots ,x_m(t)$表示$m$个传感器上的加性高斯白噪声，变量$t$代表时间。若这些加性高斯白噪声彼此不相关，并且均具有零均值向量和相同的方差${\sigma }^2$，则任何两个加性高斯白噪声之间的互协方差与互相关相同，且满足以下关系:
  
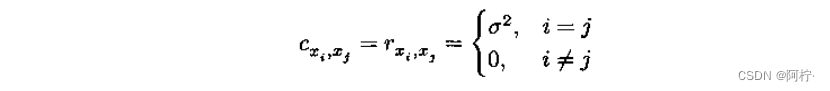
  这表明，具有零均值向量的实高斯白噪声向量x(t)的自协方差矩阵和自相关矩阵相等，并且
  
  得到实高斯白噪声向量的统计表示为
  $$Ex(t)=0$$
  $$Ex(t)x^T(t)={\sigma }^{2}I$$
• 例：令$x(t)=[x_1(t),x_2(t),\cdot \cdot \cdot ,x_m(t){]}^T$表示复正态随机向量，其中，$x_1(t),x_2(t),\cdot \cdot \cdot ,x_m(t)$表示m个传感器上的加性复高斯白噪声，它们彼此不相关，并且都具有零均值向量和相同的方差${\sigma }^2$。
  令$x_k(t)=x_{Rk}(t)+j{x}_{1k}(t)$，其中，$x_{Rk}(t)$和$x_{1k}(t)$是两个实随机过程。注意，一个复高斯白噪声过程意味着其实部$x_{Rk}(t)$和虚部$x_{1k}(t)$是两个相互独立的高斯白噪声过程，它们具有相同的方差。
  因此，$x_k(t)$为零均值和方差${\sigma }^2$的高斯白噪声过程意味着
  
  由上述条件知
  
  由于$x_1(t),\dots ,x_m(t)$是m个彼此不相关的高斯白噪声过程，故
  $$E{x}_i(t)x_j(t)=0，E{x}_i(t)x_j^{\ast }(t)=0，i\ne j$$
  综合以上条件，即可得到复高斯白噪声向量$x(t)$的统计表示为
  $$Ex(t)=0$$
  $$Ex(t)x^H(t)={\sigma }^{2}I$$
  $$Ex(t)x^T(t)=O$$