• c++学习之搜索二叉树

    目录

    一，什么是搜索二叉树？

    二，搜索二叉树的实现 

    非递归实现

    节点与类成员

    插入

    查找

    删除

     递归实现

    插入

    查找

     删除

     拷贝构造

    析构 

    赋值重载

    搜索二叉树的应用

    一，什么是搜索二叉树？

    搜索二叉树（Binary Search Tree）是一种常见的二叉树数据结构，它的每个节点都包含一个关键字，且每个节点的关键字都大于其左子树中任意节点的关键字，小于其右子树中任意节点的关键字。

    这种特性使得搜索二叉树非常适合用于查找操作。在搜索二叉树中查找一个元素时，我们可以从根节点开始，如果当前节点的值等于要查找的值，则查找成功；如果当前节点的值大于要查找的值，则在左子树中继续查找；如果当前节点的值小于要查找的值，则在右子树中继续查找.

    搜索二叉树还有一些其他的性质，例如：对于一棵有n个节点的搜索二叉树，它的高度不会超过log(n) . 这些性质使得搜索二叉树在计算机科学中有着广泛的应用，例如在数据库索引、编译器符号表等领域。

    如下就是一个二叉搜索树：

    二，搜索二叉树的实现 

    这里主要指的是实现而二叉树的增删查，搜索二叉树不能被修改。

    非递归实现

    根据搜索二叉树的特性，实现也是好比较实现的：

    到了删除，这个是比较麻烦的，因为我们不能直接删除这个节点，若为叶子节点还好，但凡这个节点但有两个孩子，删除直接会破坏搜索二叉树的结构，那么如何删除。

    用如下的搜索二叉树为例：

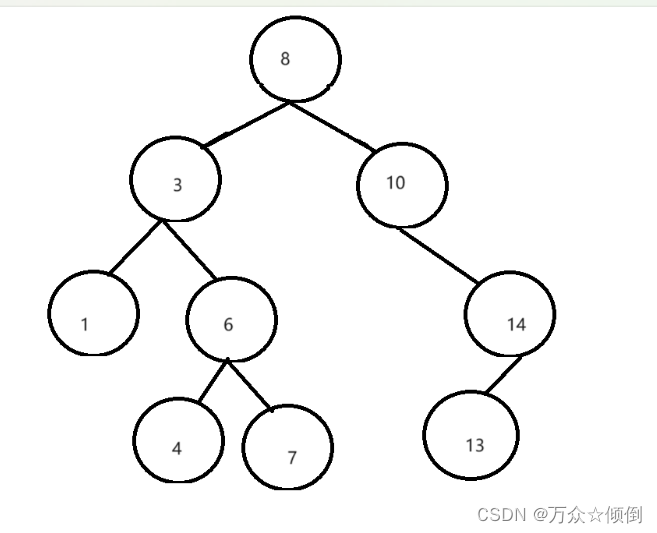
    情况一：首先对于叶子节点我们找到后可以直接删除

    情况二：删除的节点左子树为空，右子树不为空

    如这里的节点10，我们可以将它的孩子托付给它的父亲，即链接8节点的right与14节点，删除节点10。

    情况三：删除的节点右子树为空，左子树不为空

    情况三与情况四的方法类似，还是用它的父亲节点管理它的孩子节点。

    情况四：删除的节点右子树，左子树都不为空

    如这里删除节点3，上述思路就不行了。

    解决办法：替换法   

    所谓替换法就是去找一个其他节点来接管我们的孩子，如删除节点3，我么可以看到节点4可以替换3，节点1也可以替换3，虽然他也是这里的子节点，当然节点6理论可以，但它自身也有孩子。

    或者删除节点8为例，我们必须要找到一个比8节点左边都大的，且比右边的每个数最小

    总结：因此我们可以选择已该节点为起点，它的左子树中最大的节点（左边最大）节点4，右子树中最小（左子树中最右节点）节点7，这两个都可以是我们替换的对象是最为合适的。

    节点与类成员

    1. //结点的定义
    2. template<class k>struct BSTreeNOde
    3. {
    4. 	BSTreeNOde(const k& key) :_left(nullptr),_right(nullptr)
    5. 	{
    6. 		this->key = key;
    7. 	}
    8. 	BSTreeNOde<k>* _left;
    9. 	BSTreeNOde<k>* _right;
    10. 	k key;
    11. };
    12. template<class k>class BSTree
    13. {
    14. public:
    15. typedef BSTreeNOde<k>  Node;//搜索二叉树的节点
    16. //成员函数......
    17. private:
    18. 	Node* _root=nullptr;//缺省值为nullptr
    19. }

    插入

    1. //节点插入
    2. bool insert(const k& key)
    3. {
    4. 	if (_root == nullptr)
    5. 	{
    6. 		_root = new Node(key);
    7. 		return true;
    8. 	}
    9. 	Node* cur = _root;
    10. 	Node* parent = nullptr;
    11. 	while (cur)
    12. 	{
    13. 		if (key < cur->key)
    14. 		{
    15. 			parent = cur;
    16. 			cur = cur->_left;
    17. 		}
    18. 		else if (key > cur->key)
    19. 		{
    20. 			parent = cur;
    21. 			cur = cur->_right;
    22. 		}
    23. 		else
    24. 		{
    25. 			//相等就不枉搜索二叉树里插入了
    26. 			return false;
    27. 		}
    28. 	}
    29.     //cur为空的时候，即找到了合适的位置，就可以插入了
    30.     cur = new Node(key);
    31. 	//链接
    32. 	if (key > parent->key)
    33. 	{
    34. 		parent->_right = cur;
    35. 	}
    36. 	else
    37. 	{
    38. 		parent->_left = cur;
    39. 	}
    40. 	return true;
    41. }

    查找

    1. //查找
    2. bool find(const k key)
    3. {
    4. 	if (_root == nullptr)
    5. 	{
    6. 		return false;
    7. 	}
    8. 	Node* cur = _root;
    9. 	while (cur)
    10. 	{
    11. 		if (key > cur->key)
    12. 		{
    13. 			cur = cur->_right;
    14. 		}
    15. 		else if (key > cur->key)
    16. 		{
    17. 			cur = cur->left;
    18. 		}
    19. 		else
    20. 		{
    21. 			return true;
    22. 		}
    23.  
    24. 	}
    25. 	return false;
    26. }

    删除

    对于上述分析的情况，情况一就是情况二或情况三的一种，全空可以为左为空或者右为空。

    不为空时，我们这里选择替换右子树中的最小值：

    对于删除，我们这里断开和删除节点的链接即可，其次对于为空时，我们这里选择替换右子树中的最小值是分两种情况的：当我们的的右子树的第一个节点的左子树是否为空，不为空，我们去一直找最左边的，左子树为空，那么最小的就是第一个右子树节点。

    1. //删除节点
    2. bool Erase(const k& key)
    3. {
    4. 	Node* parent = nullptr;
    5. 	Node* cur = _root;
    6. 	while (cur)
    7. 	{
    8. 		if (key > cur->key)
    9. 		{
    10. 			parent = cur;
    11. 			cur = cur->_right;
    12. 		}
    13. 		else if (key < cur->key)
    14. 		{
    15. 			parent = cur;
    16. 			cur = cur->_left;
    17. 		}
    18. 		else
    19. 		{
    20. 			//开始删除 
    21. 			//叶子节点可以当作左为空或这右为空处理
    22.  
    23. 			//左为空
    24. 			if (cur->_left == nullptr)
    25. 			{
    26. 				//先判断删除的节点是否为根节点
    27. 				if (cur == _root)
    28. 				{
    29. 					//直接用孩子替换为新的根节点
    30. 					_root = cur->_right;
    31. 				}
    32. 				else
    33. 				{
    34. 					//直接让它的父亲指向它的右孩子
    35. 					if (cur == parent->_right)
    36. 					{
    37. 						parent->_right = cur->_right;
    38. 					}
    39. 					else
    40. 					{
    41. 						parent->_left = cur->_right;
    42. 					}
    43. 				}
    44. 			}
    45. 			else if (cur->_right == nullptr)
    46. 				//右为空
    47. 			{
    48. 				if (cur == _root)
    49. 				{
    50. 					//直接用孩子替换为新的根节点
    51. 					_root = cur->_left;
    52. 				}
    53. 				else
    54. 				{
    55. 					//直接让它的父亲指向它的右孩子
    56. 					if (cur == parent->_right)
    57. 					{
    58. 						parent->_right = cur->_left;
    59. 					}
    60. 					else
    61. 					{
    62. 						parent->_left = cur->_left;
    63. 					}
    64. 				}
    65. 			}
    66. 			//左右都不为空
    67. 			else
    68. 			{
    69. 				//对于这里左子树的最大（最右），右子树的最小（最左）这两个节点都可以被我们所替换
    70.  
    71. 				//找右树的最小节点（最左）
    72. 				Node* subleft = cur->_right;
    73. 				Node* parent = cur;
    74. 				if (subleft == nullptr)
    75. 				{
    76.  
    77. 					cur->_left;
    78. 				}
    79. 				while (subleft->_left)
    80. 				{
    81. 					parent = subleft;
    82. 					subleft = subleft->_left;
    83. 				}
    84. 				swap(cur->key, subleft->key);
    85. 				//此时subleft的右子树不一定为空  或者 在寻找前此时的左子树整个为空，用他的右子树链接
    86. 				if (subleft == parent->_left)
    87. 				{
    88. 					parent->_left = subleft->_right;
    89. 				}
    90. 				else
    91. 				{
    92. 					parent->_right = subleft->_right;
    93. 				}
    94. 			}
    95. 			return true;
    96. 		}
    97. 	}
    98. 	return false;
    99.  
    100. }

     递归实现

    对于增删查，不仅仅可以通过循环，我们也可以通过递归实现

    递归实现时，我们可以直接传root的引用，无需用cur来遍历，不过我们需要内部下一个函数来访问到我们的root。利用root的引用，再增加和删除时，递归到该位置我们可直接改变这个节点。

    插入

    插入的主要过程就是递归左右子树遍历直到此时的root为空，就可插入，return true。否则false。

    1. bool insertR(const k& key)
    2. 	{
    3. 		return _insertR(key, _root);
    4. 	}
    5. 	bool _insertR(const k& key, Node*& root)
    6. 	{
    7. 		if (root == nullptr)
    8. 		{
    9. 			//递归直到此时为空，链接
    10. 			root = new Node(key);
    11. 			return true;
    12. 		}
    13. 		if (root)
    14. 		{
    15. 			if (key < root->key)
    16. 			{
    17. 				return _insertR(key, root->_left);
    18. 			}
    19. 			else if (key > root->key)
    20. 			{
    21. 				return _insertR(key, root->_right);
    22. 			}
    23. 			else
    24. 			{
    25. 				//相等就不往搜索二叉树里插入了
    26. 				return false;
    27. 			}
    28. 		}
    29. 	}

    查找

    原理同上，递归的左右子树，遍历找我们需要的元素。

    1. bool findR(const k& key)
    2. 	{
    3. 		return _findR(_root,key);
    4. 	}
    5. 	bool _findR(Node* root, const k& key)
    6. 	{
    7. 		if (root == nullptr)
    8. 		{
    9. 			return false;
    10. 		}
    11.  
    12. 		if (root->key < key)
    13. 		{
    14. 			return _findR(root->_right, key);
    15. 		}
    16. 		else if (root->key > key)
    17. 		{
    18. 			return _findR(root->_left, key);
    19. 		}
    20. 		else
    21. 		{
    22. 			return true;
    23. 		}
    24. 	}

     删除

    因为循环时无法复用我们在当左子树右子树都不为空时，我们去找右子树的最小值，即右树的最左值，循环右数的左子树的最左直到为空，交换之后，开始删除，我们想要服用左子树为空的删除问题，但此时的父亲不一样，我们不能去服用。

    但对于递归，当我们要去找右子树的最左孩子，找到之后交换，然后变成子问题递归，左子树为空删除。

    1. bool EraseR(const k& key)
    2. 	{
    3. 		_EraseR(_root, key)
    4. 	}
    5. 	bool _EraseR(Node*& root, const k& key)
    6. 	{
    7. 		if (root == nullptr)
    8. 			return false;
    9. 	
    10. 		if (root->_key < key)
    11. 		{
    12. 			return _EraseR(root->_right, key);
    13. 		}
    14. 		else if (root->_key > key)
    15. 		{
    16. 			return _EraseR(root->_left, key);
    17. 		}
    18. 		else
    19. 		{
    20. 			// 删除
    21. 			if (root->_left == nullptr)
    22. 			{
    23. 				Node* del = root;
    24. 				root = root->_right;
    25. 				delete del;
    26. 	
    27. 				return true;
    28. 	
    29. 			}
    30. 			else if (root->_right == nullptr)
    31. 			{
    32. 				Node* del = root;
    33. 				root = root->_left;
    34. 				delete del;
    35. 	
    36. 				return true;
    37. 			}
    38. 			else
    39. 			{
    40. 				Node* subLeft = root->_right;
    41. 				while (subLeft->_left)
    42. 				{
    43. 					subLeft = subLeft->_left;
    44. 				}
    45. 	
    46. 				swap(root->_key, subLeft->_key);
    47. 	
    48. 				// 转换成在子树去递归删除
    49. 				return _EraseR(root->_right, key);
    50. 			}
    51. 		}

     拷贝构造

    析构 

    1.  
    2. 	~BSTree()
    3. 	{
    4. 		Destory(_root);
    5. 	}
    6. //递归删除左右节点
    7. 	void Destroy(Node*& root)
    8. 	{
    9. 		if (root == nullptr)
    10. 		{
    11. 			return;
    12. 		}
    13. 		Destroy(root->_left);
    14. 		Destroy(root->_right);
    15. 		delete root;
    16. 		root = nullptr;
    17. 	}

    赋值重载

    1. //赋值重载
    2. 	void operator=(const BSTree<k>& x)
    3. 	{
    4. 		swap(_root, x._root);
    5. 		return *this;
    6. 	}

    搜索二叉树的应用

    在上述我们基本上已经掌握了搜索二叉树的性质，对于一个搜索树，那么效率当然至关重要，然而实际上搜索二叉树的查找效率最慢就是线性查找，时间复杂度O(N)，最快也是很难达O(logn）,因为搜索二叉树在创建时，你是无法保证左右子树是接近满二叉树或者完全二叉树的，因此效率是得不到保证的。故此我们需要在搜索二叉树的基础上做一些平衡：

    平衡方案：

    1.红黑树

    2.AVL树

    这些我们之后了解，现在我们先了解一下key的搜索模型：

    key_value模型，通过key值，寻找对应的value。此时整个二叉搜素书的结构不变，只是在此基础上增加一个模板参数value：

    1.  
    2. 	template<class k,class v>struct BSTreeNOde
    3. 	{
    4. 		BSTreeNOde(const k& key, const v& value) :_left(nullptr), _right(nullptr),
    5. 			this->key(key),this>value(value)
    6. 		{}
    7. 		BSTreeNOde<k, v>* _left;
    8. 		BSTreeNOde<k, v>* _right;
    9. 		k key;
    10. 		v value;
    11. 	};
    12.  
    13.  
    14. 	template<class k, class v>class BSTree
    15. 	{
    16. 	public:
    17. 		typedef BSTreeNOde<k, v> Node;
    18. 		bool insertR(const k& key, const v& value)
    19. 	    {
    20. 		  return _insertR(key, _root, value);
    21. 	    }
    22. 		bool _insertR(const k& key, Node*& root, const v& value)
    23. 		{
    24. 			if (root == nullptr)
    25. 			{
    26. 				//递归直到此时为空，链接
    27. 				root = new Node(key,value);
    28. 				return true;
    29. 			}
    30. 			if (root)
    31. 			{
    32. 				if (key < root->key)
    33. 				{
    34. 					return _insertR(key, root->_left);
    35. 				}
    36. 				else if (key > root->key)
    37. 				{
    38. 					return _insertR(key, root->_right);
    39. 				}
    40. 				else
    41. 				{
    42. 					//相等就不往搜索二叉树里插入了
    43. 					return false;
    44. 				}
    45. 			}
    46. 		}
    47. 		Node* findR(const k& key)
    48. 		{
    49. 			return _findR(_root, key);
    50. 		}
    51. 		Node* _findR(Node* root, const k& key)
    52. 		{
    53. 			if (root == nullptr)
    54. 			{
    55. 				return nullptr;
    56. 			}
    57.  
    58. 			if (root->key < key)
    59. 			{
    60. 				return _findR(root->_right, key);
    61. 			}
    62. 			else if (root->key > key)
    63. 			{
    64. 				return _findR(root->_left, key);
    65. 			}
    66. 			else
    67. 			{
    68. 				return root;
    69. 			}
    70. 		}
    71.  
    72. 	private:
    73. 	Node* _root = nullptr;
    74.  
    75. 	};

    实际上对应的修改也只有微小的两部分，一部分是增加一个值value，一部分是插入的时候增加这个参数并且查找的时候返回类型修改为节点型，这样我们就可以访问到其中的数据。

    通过这种方式我们就可以实现门禁系统，传入的信息在搜索树中寻找，找到对应的人物。

    当然这里的value我们可以控制他的个数和他的作用，它也可以用来统计个数，其他标志等。

    (在搜索的时候value值++，来记录次数)。我们可以通过key值寻找对应的value 值，或者反过来都行。

  • 相关阅读:
    中国设备工程杂志中国设备工程杂志社中国设备工程编辑部2022年第18期目录
    计算机毕业设计(55)php小程序毕设作品之企业公司小程序系统
    K8s笔记
    动态SQL
    仿真科普｜CAE技术赋能无人机 低空经济蓄势起飞
    数据库上机实验4 数据更新和视图
    如何使用nginx部署https网站（亲测可行）
    微服务之Nacos注册管理
    threejs绘制多个多边形
    通过 Pulsar 源码彻底解决重复消费问题
  • 原文地址：https://blog.csdn.net/qq_61422622/article/details/134019494