• 二叉搜索树（从0-1手把手讲解）

    一、概念

    二、基本操作实现

    准备工作：

    1、查找元素

    2、插入元素

    三、删除元素

            一、所要删除的元素需要先找到这个节点所在的位置

            二、分情况讨论所要删除元素左右树的情况（是否为null）

            三、如果左右树都不为null，删除节点位置应该置为什么？

     1.1、寻找所要删除的节点

    2.1、讨论删除节点左右树的情况

    完整代码：

    一、概念


            二叉搜索树又称二叉排序树，是一种可以进行快速查询的二叉树类型。

    所具有的性质：

    • 若节点不为空，根节点的值大于其左子树任一节点的值。
    • 若节点不为空，根节点的值小于其右子树任一节点的值。
    • 任一节点的左右子树均为二叉搜索树

    其性质的特点在于中序遍历的结果一定是升序的（如下图）

     

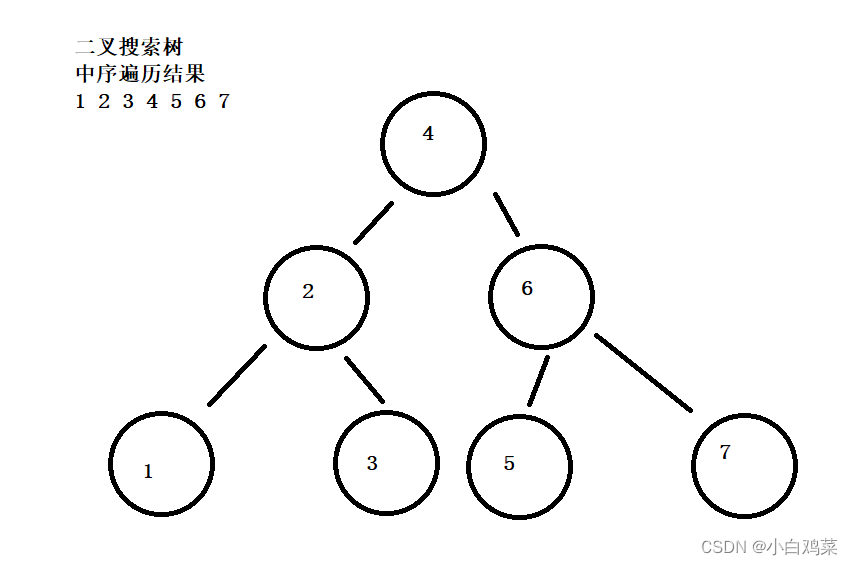
    二、基本操作实现

    准备工作：

            创建二叉树结点，以及根节点：

    1. //创建二叉树结点
    2. public static class Node{
    3.         int val;
    4.         Node left;
    5.         Node right;
    6.         public Node(int val) {
    7.             this.val = val;
    8.         }
    9.     }
    10.     //根节点
    11.     private static Node root =null;

    1、查找元素

            思路：结合二叉搜索树的特性，节点的左树节点值都比其小，右树节点都比其大的特性，我们从根节点的值与寻找元素比较，如果根节点小就向右树进行寻找，反之向左树寻找。

    1. //查询元素
    2.     public Node search(int key) {
    3.         if (root == null) {
    4.             return null;
    5.         }
    6.         //定义一个遍历节点
    7.         Node cur = root;
    8.         while (cur != null) {
    9.             //寻找到返回节点
    10.             if (key == cur.val) {
    11.                 return cur;
    12.                 //节点值小时向右树寻找
    13.             }else if (key > cur.val) {
    14.                 cur = cur.right;
    15.                 //节点值大时向左树寻找
    16.             } else {
    17.                 cur = cur.left;
    18.             }
    19.         }
    20.         return null;
    21.     }

    2、插入元素

            思路：同样结合二叉搜索树的特性，节点的左树节点值都比其小，右树节点都比其大的特性。用cur节点去遍历二叉树，如果插入元素大于节点值就向树的右边遍历，反之向左边遍历。找到合适的位置即可（插入的元素一定都是放在叶子节点上）

            为什么插入的元素一定在叶子节点上呢？

    这里的8是我们插入的元素，为什么会放在叶子节点上？是因为我们这个元素要不是比节点小要不就是大（二叉搜索树不可以包含相同的元素）并且不会存在大小相同的元素，那么他就会一直遍历下去寻找要插入的位置直到叶子节点结束（相对于叶子节点要不大就放在叶子右边要不小就放在叶子左边） 

    1.     public boolean insert(int key) {
    2.         if (root == null) {
    3.             root = new Node(key);
    4.             return true;
    5.         }
    6.         //cur为遍历节点
    7.         Node cur = root;
    8.         //因为cur一直遍历最后会变成null无法找到上一个节点
    9.         //所以创建一个parent标记cur上一个节点
    10.         Node parent = null;
    11.         while (cur != null) {
    12.             //插入元素比节点值大向右遍历
    13.             if (cur.val > key) {
    14.                 parent = cur;
    15.                 cur = cur.left;
    16.                 //插入元素比节点值小向左遍历
    17.             } else if (cur.val < key) {
    18.                 parent = cur;
    19.                 cur = cur.right;
    20.             } else return false;
    21.         }
    22.         Node node = new Node(key);
    23.         if (parent.val < key) {
    24.             parent.right = node;
    25.         } else {
    26.             parent.left = node;
    27.         }
    28.         return true;
    29.     }

    三、删除元素

            所要考虑的问题：

            一、所要删除的元素需要先找到这个节点所在的位置

            二、分情况讨论所要删除元素左右树的情况（是否为null）

            三、如果左右树都不为null，删除节点位置应该置为什么？

     1.1、寻找所要删除的节点

            思路：我们需要遍历二叉搜索树，寻找所要找的节点记录下来，并且记录下它的上一个节点（因为在删除当前节点后，需要让上一个节点与删除节点的下一个节点做链接）。如果找到这个节点就调用removeNode方法去做我们的删除节点操作。

    1.    public void remove(int key) {
    2.         //遍历节点
    3.         Node cur = root;
    4.         //遍历节点的上一个节点
    5.         Node parent = null;
    6.         while (cur != null) {
    7.             if (cur.val < key) {
    8.                 parent = cur;
    9.                 cur = cur.right;
    10.             } else if (cur.val >key) {
    11.                 parent = cur;
    12.                 cur = cur.left;
    13.             } else {
    14.                 removeNode(cur,parent);
    15.  
    16.                 System.out.println(key+"所在结点删除成功");
    17.                 return;
    18.             }
    19.         }
    20.     }

    2.1、讨论删除节点左右树的情况

            所有情况：

    1、删除节点的左节点为空（可能为根节点）

    1. if (cur.left == null) {
    2.             if (cur == root) {
    3.                 root = root.right;
    4.             } else if(cur == parent.left) {
    5.                 parent.left = cur.right;
    6.             } else {
    7.                 parent.right = cur.right;
    8.             }

    2、删除节点的右节点为空（可能为根节点）

    1. if (cur.right == null) {
    2.             if (cur == root) {
    3.                 root = root.left;
    4.             } else if (cur == parent.left) {
    5.                 parent.left = cur.left;
    6.             } else  {
    7.                 parent.right = cur.left;
    8.             }

    3、删除节点左右树不为空（可能为根节点）

    替代的节点只能是：

    删除节点左树中最大的节点（最右下边的节点）

    删除节点右数中最小的节点（最左下的节点）

            先上代码下面详解

    1.  Node tParent = cur;
    2.             Node t = cur.right;
    3.             while (t.left != null) {
    4.                 tParent = t;
    5.                 t = t.left;
    6.             }
    7.             cur.val = t.val;
    8.             if (tParent.right == t) {
    9.                 tParent.right = t.right;
    10.             } else {
    11.                 tParent.left = t.right;
    12.             }

    4、删除节点为null（不存在）

    1. if (cur==null) {
    2.             return;
    3.         }

    删除节点左右树不为空的情况是我们最难理解的。先看下面的图

     

    先看7和11的位置。7是 删除节点9作数中最大值的节点，11是删除节点9的右树中最小值的节点。

    替代的节点只能是：

    删除节点左树中最大的节点（最右下边的节点）

    删除节点右数中最小的节点（最左下的节点）

    因为节点的左数比其都小，右树都比其大的特性（仔细理解这个话）。只有这两个与删除节点最近值的节点才能代替删除的节点。

    完整代码：

    1. public class BinarySearchTree {
    2.     public static void main(String[] args) {
    3.         BinarySearchTree binarySearchTree = new BinarySearchTree();
    4.         binarySearchTree.insert(8);
    5.         binarySearchTree.insert(12);
    6.         binarySearchTree.insert(3);
    7.         binarySearchTree.insert(6);
    8.         binarySearchTree.insert(9);
    9.         binarySearchTree.insert(1);
    10.         binarySearchTree.insert(13);
    11.         System.out.println();
    12.         binarySearchTree.order(root);
    13.         binarySearchTree.remove(8);
    14.         binarySearchTree.order(root);
    15.  
    16.     }
    17.  
    18.  
    19.  
    20.     public static class Node{
    21.         int val;
    22.         Node left;
    23.         Node right;
    24.         public Node(int val) {
    25.             this.val = val;
    26.         }
    27.     }
    28.     //根节点
    29.     private static Node root =null;
    30.  
    31.     //插入元素
    32.  
    33.     /**
    34.      *
    35.      * @param key 搜索树的性质不能有重复的值
    36.      * @return 是否成功
    37.      */
    38.     public boolean insert(int key) {
    39.         if (root == null) {
    40.             root = new Node(key);
    41.             return true;
    42.         }
    43.         //cur为遍历节点
    44.         Node cur = root;
    45.         //因为cur一直遍历最后会变成null无法找到上一个节点
    46.         //所以创建一个parent标记cur上一个节点
    47.         Node parent = null;
    48.         while (cur != null) {
    49.             //插入元素比节点值大向右遍历
    50.             if (cur.val > key) {
    51.                 parent = cur;
    52.                 cur = cur.left;
    53.                 //插入元素比节点值小向左遍历
    54.             } else if (cur.val < key) {
    55.                 parent = cur;
    56.                 cur = cur.right;
    57.             } else return false;
    58.         }
    59.         Node node = new Node(key);
    60.         if (parent.val < key) {
    61.             parent.right = node;
    62.         } else {
    63.             parent.left = node;
    64.         }
    65.         return true;
    66.     }
    67.  
    68.  
    69.     //查询元素
    70.     public Node search(int key) {
    71.         if (root == null) {
    72.             return null;
    73.         }
    74.         //定义一个遍历节点
    75.         Node cur = root;
    76.         while (cur != null) {
    77.             //寻找到返回节点
    78.             if (key == cur.val) {
    79.                 return cur;
    80.                 //节点值小时向右树寻找
    81.             }else if (key > cur.val) {
    82.                 cur = cur.right;
    83.                 //节点值大时向左树寻找
    84.             } else {
    85.                 cur = cur.left;
    86.             }
    87.         }
    88.         return null;
    89.     }
    90.  
    91.     public void order(Node node) {
    92.         if (node == null) {
    93.             return;
    94.         }
    95.         order(node.left);
    96.         System.out.print(node.val+" ");
    97.         order(node.right);
    98.     }
    99.     //删除元素
    100.     public void remove(int key) {
    101.         //遍历节点
    102.         Node cur = root;
    103.         //遍历节点的上一个节点
    104.         Node parent = null;
    105.         while (cur != null) {
    106.             if (cur.val < key) {
    107.                 parent = cur;
    108.                 cur = cur.right;
    109.             } else if (cur.val >key) {
    110.                 parent = cur;
    111.                 cur = cur.left;
    112.             } else {
    113.                 removeNode(cur,parent);
    114.  
    115.                 System.out.println(key+"所在结点删除成功");
    116.                 return;
    117.             }
    118.         }
    119.     }
    120.     public void removeNode(Node cur,Node parent) {
    121.         //删除元素左边为null
    122.         if (cur==null) {
    123.             return;
    124.         }
    125.         if (cur.left == null) {
    126.             if (cur == root) {
    127.                 root = root.right;
    128.             } else if(cur == parent.left) {
    129.                 parent.left = cur.right;
    130.             } else {
    131.                 parent.right = cur.right;
    132.             }
    133.         } else if (cur.right == null) {
    134.             if (cur == root) {
    135.                 root = root.left;
    136.             } else if (cur == parent.left) {
    137.                 parent.left = cur.left;
    138.             } else  {
    139.                 parent.right = cur.left;
    140.             }
    141.         } else {
    142.             Node tParent = cur;
    143.             Node t = cur.right;
    144.             while (t.left != null) {
    145.                 tParent = t;
    146.                 t = t.left;
    147.             }
    148.             cur.val = t.val;
    149.             if (tParent.right == t) {
    150.                 tParent.right = t.right;
    151.             } else {
    152.                 tParent.left = t.right;
    153.             }
    154.         }
    155.  
    156.     }
    157.  
    158. }

  • 相关阅读:
    jedis:使用事务开启watch监控
    react是否支持给标签设置自定义的属性，比如给video标签设置webkit-playsinline？
    洛科威多功能岩棉板助力节能减碳战略，推动碳达峰目标实现
    对CMSIS的学习（第4-5部分）
    vue实现酷炫可视化大屏
    Edge浏览器没有让我失望! 今天终于可以在win10中模拟IE内核进行前端测试了!
    人工智能 | ShowMeAI资讯日报 #2022.06.26
    用C语言实现，点亮小灯，让其闪烁
    使用 zk-SNARK 的可编程零知识证明：第 1 部分
    开源大数据组件
  • 原文地址：https://blog.csdn.net/weixin_63426509/article/details/127134938