《Python 计算机视觉编程》学习笔记（四）

第 4 章 照相机模型与增强现实

引言

本章中我们将会讲述如何确定照相机的参数，以及在具体应用中，如增强现实，如何使用图像间的投影变换。

4.1　针孔照相机模型

针孔照相机模型（有时称为射影照相机模型）是计算机视觉中广泛使用的照相机模型。对于大多数应用来说，针孔照相机模型简单，并且具有足够的精确度。这个名字来源于一种类似暗箱机的照相机。该照相机从一个小孔采集射到暗箱内部的光线。在针孔照相机模型中，在光线投影到图像平面之前，从唯一一个点经过，也就是照相机中心 C。图 4-1 为从照相机中心前画出图像平面的图解。

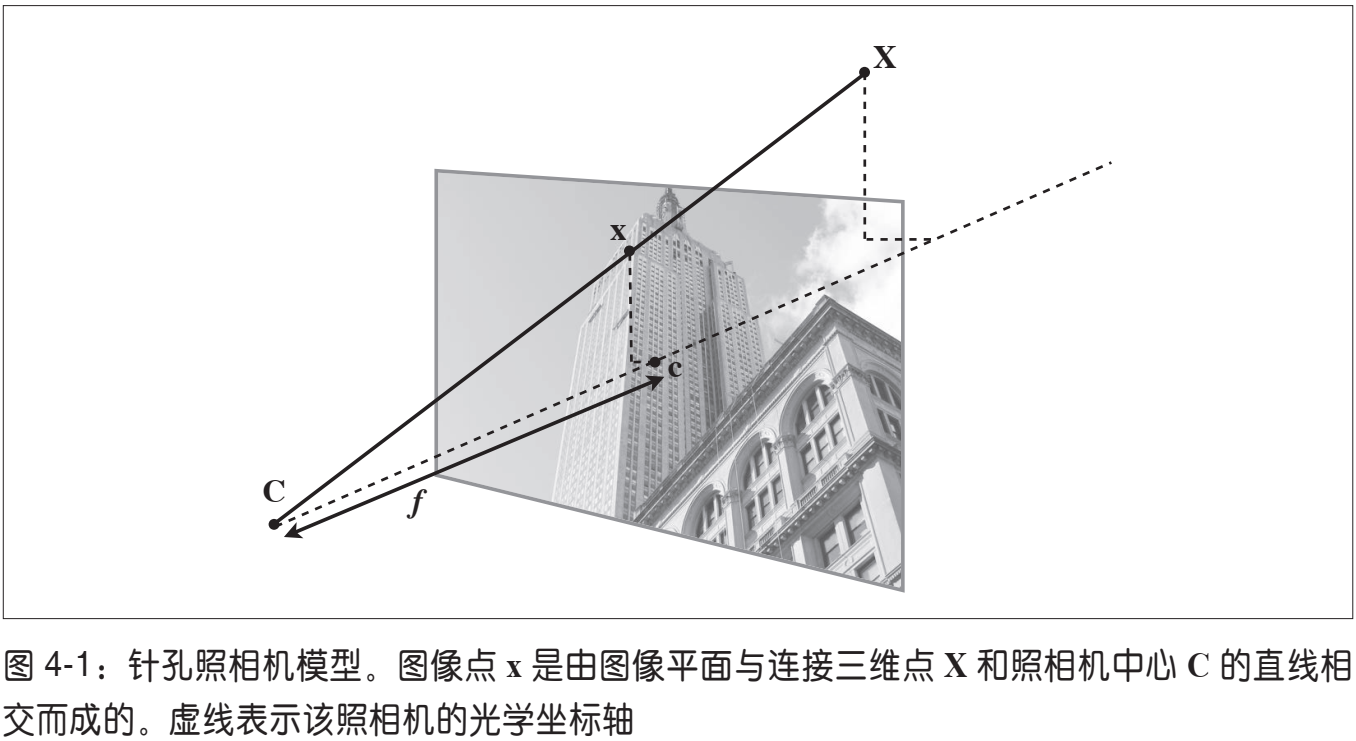
由图像坐标轴和三维坐标系中的 x 轴和 y 轴对齐平行的假设，我们可以得出针孔照相机的投影性质。照相机的光学坐标轴和 z 轴一致，该投影几何可以简化成相似三角形。在投影之前通过旋转和平移变换，对该坐标系加入三维点，会出现完整的投影变换。

在针孔照相机中，三维点 X 投影为图像点 x（两个点都是用齐次坐标表示的），如下所示：
$$\lambda \mathbf{x}=\mathbf{PX}$$

注意，在齐次坐标系中，三维点 X 的坐标由 4 个元素组成， X=[X, Y, Z, W]。这里的标量 λ 是三维点的逆深度。如果我们打算在齐次坐标中将最后一个数值归一化为 1，那么就会使用到它。

照相机矩阵

照相机矩阵可以分解为:
$$\mathbf{P}=K[\mathbf{R}\mid \mathbf{t}]$$

R 是描述照相机方向的旋转矩阵， t 是描述照相机中心位置的三维平移向量，内标定矩阵 K 描述照相机的投影性质。

标定矩阵仅和照相机自身的情况相关，通常情况下可以写成：
K = [ α f s c x 0 f c y 0 0 1 ] \boldsymbol{K}=\left[

\right] K=⎣ ⎡​αf00​sf0​cx​cy​1​⎦ ⎤​

图像平面和照相机中心间的距离为焦距 f。当像素数组在传感器上偏斜的时候，需要用到倾斜参数 s。在大多数情况下， s 可以设置成 0。也就是说：
K = [ f x 0 c x 0 f y c y 0 0 1 ] \boldsymbol{K}=\left[

\right] K=⎣ ⎡​fx​00​0fy​0​cx​cy​1​⎦ ⎤​
我们使用了另外的记号 $f_x$和$f_y$，两者关系为$f_x$=$\alpha f_y$。
纵横比例参数 α 是在像素元素非正方形的情况下使用的。通常情况下，我们可以默认设置 α=1。经过这些假设，标定矩阵变为:
K = [ f 0 c x 0 f c y 0 0 1 ] \boldsymbol{K}=\left[

f0cx0fcy001" role="presentation">f000f0cxcy1$$\begin{array}{llc}f& 0& c_x\\ 0& f& c_y\\ 0& 0& 1\end{array}$$

\right] K=⎣ ⎡​f00​0f0​cx​cy​1​⎦ ⎤​

除焦距之外，标定矩阵中剩余的唯一参数为光心（有时称主点）的坐标 c=$[c_x，c_y]$，也就是光线坐标轴和图像平面的交点。因为光心通常在图像的中心，并且图像的坐标是从左上角开始计算的，所以光心的坐标常接近于图像宽度和高度的一半。特别强调一点，在这个例子中，唯一未知的变量是焦距$f$。

三维点的投影

数据集暂时没找到。代码暂时先不调整了。啥不写有点空。放一段代码吧！

from scipy import linalg
class Camera(object):
    """ 表示针孔照相机的类 """
    def __init__(self,P):
        """ 初始化 P = K[R|t] 照相机模型 """
        self.P = P
        self.K = None # 标定矩阵
        self.R = None # 旋转
        self.t = None # 平移
        self.c = None # 照相机中心

    def project(self,X):
        """ X( 4xn 的数组)的投影点，并且进行坐标归一化 """
        x = dot(self.P,X)
        for i in range(3):
            x[i] /= x[2]
        return x
        
    def rotation_matrix(a):
        """创建一个用于围绕向量a轴旋转的三维旋转矩阵"""
        R = eye(4)
        R[:3,:3] = linalg.expm([0,-a[2],a[1]],[a[2],0,-a[0]],[-a[1],a[0],0])
        return R

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

照相机矩阵的分解

如果给定如方程$\lambda \mathbf{x}=\mathbf{PX}$（ 4.2）所示的照相机矩阵 P，我们需要恢复内参数 K 以及照相机的位置 t 和姿势 R。矩阵分块操作称为因子分解。这里，我们将使用一种矩阵因子分解的方法，称为 RQ 因子分解。

RQ 因子分解的结果并不是唯一的。在该因子分解中，分解的结果存在符号二义性。由于我们需要限制旋转矩阵 R 为正定的（否则，旋转坐标轴即可），所以如果需要，我们可以在求解到的结果中加入变换 T 来改变符号。

from scipy import linalg
import time 
from PIL import Image
from numpy import *
import matplotlib.font_manager as fm
import os
from scipy import linalg


#定义字体模板
myfont=fm.FontProperties(fname='C:/Windows/Fonts/simsun.ttc') 

def get_imlist(path):
    """ 
        函数功能：获得path路径下后缀为 .jpg的图片完整路径
        参数说明: path__图片存储路径
        函数返回：返回path路径下的所有的图片的完整路径
    """
    imlist = []
    for f in os.listdir(path):
        if f.endswith('.jpg'):
            # 将新获得的图片名称加上路径添加到名称列表中
            imlist.append(os.path.join(path,f))

    return imlist


class Camera(object):
    """ 表示针孔照相机的类 """
    def __init__(self,P):
        """ 初始化 P = K[R|t] 照相机模型 """
        self.P = P
        self.K = None # 标定矩阵
        self.R = None # 旋转
        self.t = None # 平移
        self.c = None # 照相机中心

    def project(self,X):
        """ X( 4xn 的数组)的投影点，并且进行坐标归一化 """
        x = dot(self.P,X)
        for i in range(3):
            x[i] /= x[2]
        return x

    def rotation_matrix(a):
        """创建一个用于围绕向量a轴旋转的三维旋转矩阵"""
        R = eye(4)
        #分割出第三行以前的行和第三列以前的列的所有元素
        R[:3,:3] = linalg.expm([[0,-a[2],a[1]],[a[2],0,-a[0]],[-a[1],a[0],0]])
        return R
   
    def factor(self):
        """将照相机矩阵分解为 K,R,t,其中, R=K[R|t]"""

        # 分解前3×3的部分
        K,R = linalg.rq(self.P[:,:3])
        # 将K的对角线元素设为正值
        T = diag(sign(diag(K)))
        if linalg.det(T) < 0:
            T[1,1] *= -1
        self.K = dot(K,T)
        self.R = dot(T,R)   # T的逆矩阵为其自身
        self.t = dot(linalg.inv(self.K), self.P[:,3])
        
        return self.K, self.R, self.t

def main():

    K = array([[1000,0,500],[0,1000,300],[0,0,1]])
    tmp = Camera.rotation_matrix([0,0,1])[:3,:3]
    # hstack将参数元组的元素数组按水平方向进行叠加
    Rt = hstack((tmp,array([[50],[40],[30]])))
    cam = Camera(dot(K,Rt))

    print(K,Rt)
    print(cam.factor())

    return

if __name__=='__main__':
    startTime = time.time()
    main()
    endTime = time.time()
    print("the program running time is :",endTime - startTime)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

输出结果，照相机矩阵分解的效果如下：

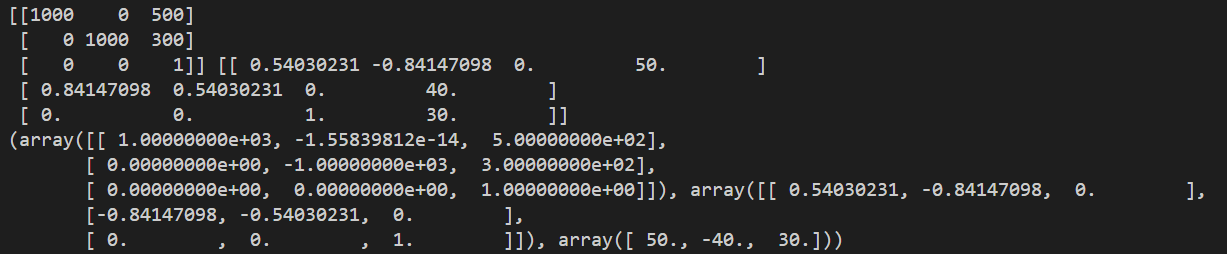
计算照相机中心

给定照相机投影矩阵 P，我们可以计算出空间上照相机的所在位置。照相机的中心C，是一个三维点，满足约束 PC=0。对于投影矩阵为$P=K[R|t]$ 的照相机，有：
$$\mathbf{K}[\mathbf{R}\mid \mathbf{t}]\mathbf{C}=\mathbf{K}\mathbf{RC}+\mathbf{K}\mathbf{t}=0$$

照相机的中心可以由下述式子来计算：
$$\mathbf{C}=-{\mathbf{R}}^T\mathbf{t}$$

照相机的中心和内标定矩阵 K 无关。

4.2 照相机标定

标定照相机是指计算出该照相机的内参数。在我们的例子中，是指计算矩阵 K。标定照相机的标准方法是，拍摄多幅平面棋盘模式的图像，然后进行处理计算。

为什么需要照相机标定呢？
这是由于每个镜头的畸变程度各不相同，通过照相机标定可以校正这种镜头畸变。其实可以认为用这种标定的方式来求解照相机内参和畸变参数，相当于一种照相机校准，然后这些参数就可以用于后面的求解。例如求解新拍的两幅图片相对的 R和 t ，求解这个外参用到就是标定得到的相机内参和畸变参数。

一个简单的标定方法

大多数参数可以使用基本的假设来设定（正方形垂直的像素，光心位于图像中心），比较难处理的是获得正确的焦距。需要准备一个平面矩形的标定物体（一个书本即可）、用于测量的卷尺和直尺，以及一个平面。

下面是具体操作步骤：

• 测量你选定矩形标定物体的边长 dX 和 dY；
• 将照相机和标定物体放置在平面上，使得照相机的背面和标定物体平行，同时物体位于照相机图像视图的中心，你可能需要调整照相机或者物体来获得良好的对 齐效果；
• 测量标定物体到照相机的距离 dZ；
• 拍摄一副图像来检验该设置是否正确，即标定物体的边要和图像的行和列对齐； • 使用像素数来测量标定物体图像的宽度和高度 $d_x和d_y$。
  实验设置情况如图 4-3 所示。现在，使用下面的相似三角形（参见图 4-1）关系可以获得焦距：
  $$f_x=\frac{\mathrm{d}x}{\mathrm{d}X}\mathrm{d}Z,f_y=\frac{\mathrm{d}y}{\mathrm{d}Y}\mathrm{d}Z$$
  
  对于如图 4-3 所示的特定设置，物体宽度和高度的测量值分别为 130 mm 和 185 mm，则， dX=130， dY=185。从照相机到物体的距离为 460 mm，则 dZ=460。你可以使用任意的测量单位，只有测量值的比例才影响最终焦距的计算。图像中物体的宽度和高度分别为 722 和 1040 像素。将这些值代入上面的关系表达式可以获得焦距的大小：

$$f_x=2555,f_y=2586$$

值得注意的是，我们现在获取的焦距是在特定图像分辨率下计算出来的。在这个例子中，图像大小为 2592× 1936 像素。记住，焦距和光心是使用像素来度量的，其尺度和图像分辨率相关。如果你使用其他的图像分辨率来拍摄（例如，一个缩略图像），那么这些值都会改变。

4.3　以平面和标记物进行姿态估计

在第 3 章中，我们学习了如何从平面间估计单应性矩阵。如果图像中包含平面状的标记物体，并且已经对照相机进行了标定，那么我们可以计算出照相机的姿态（旋转和平移）。这里的标记物体可以为对任何平坦的物体。

提取两幅图像的 SIFT 特征，然后使用 RANSAC 算法稳健地估计单应性矩阵。单应性矩阵将一幅图像中标记物（在这个例子中，标记物是指书本）上的点映射到另一幅图像中的对应点。下面我们定义相应的三维坐标系，使标记物在 X-Y 平面上（ Z=0），原点在标记物的某位置上。为了检验单应性矩阵结果的正确性，我们需要将一些简单的三维物体放置在标记物上，这里我们使用一个立方体。

def cube_points(c, wid):
    """ Creates a list of points for plotting
        a cube with plot. (the first 5 points are
        the bottom square, some sides repeated). """
    p = []
    # bottom
    p.append([c[0] - wid, c[1] - wid, c[2] - wid])
    p.append([c[0] - wid, c[1] + wid, c[2] - wid])
    p.append([c[0] + wid, c[1] + wid, c[2] - wid])
    p.append([c[0] + wid, c[1] - wid, c[2] - wid])
    p.append([c[0] - wid, c[1] - wid, c[2] - wid])  # same as first to close plot

    # top
    p.append([c[0] - wid, c[1] - wid, c[2] + wid])
    p.append([c[0] - wid, c[1] + wid, c[2] + wid])
    p.append([c[0] + wid, c[1] + wid, c[2] + wid])
    p.append([c[0] + wid, c[1] - wid, c[2] + wid])
    p.append([c[0] - wid, c[1] - wid, c[2] + wid])  # same as first to close plot

    # vertical sides
    p.append([c[0] - wid, c[1] - wid, c[2] + wid])
    p.append([c[0] - wid, c[1] + wid, c[2] + wid])
    p.append([c[0] - wid, c[1] + wid, c[2] - wid])
    p.append([c[0] + wid, c[1] + wid, c[2] - wid])
    p.append([c[0] + wid, c[1] + wid, c[2] + wid])
    p.append([c[0] + wid, c[1] - wid, c[2] + wid])
    p.append([c[0] + wid, c[1] - wid, c[2] - wid])

    return array(p).T

def make_homog(points):
    """ Convert a set of points (dim*n array) to 
        homogeneous coordinates. """
        
    return vstack((points,ones((1,points.shape[1])))) 

from PCV.geometry import homography,camera

def postureEstimates():
    """ 
        函数功能：姿态估计
        参数说明: 无
        函数返回：无
    """  
    #  计算特征
    harris.process_image('picture/book_frontal.jpg', 'im0.sift')
    l0, d0 = harris.read_features_from_file('im0.sift')

    harris.process_image('picture/book_perspective.jpg', 'im1.sift')
    l1, d1 = harris.read_features_from_file('im1.sift')


    #  匹配特征并计算单应性矩阵
    matches = harris.match_twosided(d0, d1)
    ndx = matches.nonzero()[0]
    fp = make_homog(l0[ndx, :2].T)
    ndx2 = [int(matches[i]) for i in ndx]
    tp = make_homog(l1[ndx2, :2].T)

    model = homography.RansacModel()
    H, inliers = homography.H_from_ransac(fp, tp, model)

    # 计算照相机标定矩阵
    K = my_calibration((400, 300))

    # 位于边长为0.2 z=0平面的三维点
    box = cube_points([0, 0, 0.1], 0.1)

    # 投影第一幅图像上底部的正方形
    cam1 = camera.Camera(hstack((K, dot(K, array([[0], [0], [-1]])))))
    # 底部正方形上的点
    box_cam1 = cam1.project(homography.make_homog(box[:, :5]))


    # 使用H将点变换到第二幅图像中
    box_trans = homography.normalize(dot(H,box_cam1))

    # 从cam1和H中计算第二个照相机矩阵
    cam2 = camera.Camera(dot(H, cam1.P))
    A = dot(linalg.inv(K), cam2.P[:, :3])
    A = array([A[:, 0], A[:, 1], cross(A[:, 0], A[:, 1])]).T
   
    cam2.P[:, :3] = dot(K, A)

    # 使用第二个照相机矩阵投影
    box_cam2 = cam2.project(homography.make_homog(box))

    # plotting
    im0 = array(Image.open('picture/book_frontal.jpg'))
    im1 = array(Image.open('picture/book_perspective.jpg'))

    figure()
    subplot(221)
    imshow(im0)
    plot(box_cam1[0, :], box_cam1[1, :], linewidth=3,color= 'r')
    title('2D projection of bottom square')
    axis('off')

    subplot(222)
    imshow(im1)
    plot(box_trans[0, :], box_trans[1, :], linewidth=3,color= 'r')
    title('2D projection transfered with H') ,axis('off')
    
    subplot(2,1,2)
    imshow(im1)
    plot(box_cam2[0, :], box_cam2[1, :], linewidth=3,color= 'r')
    title('3D points projected in second image'),axis('off')
    
    # subplots_adjust(top=1, bottom=0, right=1, left=0, hspace=0, wspace=0)
    margins(0, 0)
    savefig('output/test1.jpg',dpi = 600, bbox_inches='tight', pad_inches=1)
    show()

    return

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116

输出图像如下：

上面估计方法是，使用平面物体作为标记物，来计算用于新视图投影矩阵。将图像的特征和对齐后的标记匹配，计算出单应性矩阵，然后用于计算照相机的姿态。在选择照片是要选择合适的尺寸，否则绘制出来的长方形会变形。

4.4　增强现实

增强现实（ Augmented Reality， AR）是将物体和相应信息放置在图像数据上的一系列操作的总称。最经典的例子是放置一个三维计算机图形学模型，使其看起来属于该场景；如果在视频中，该模型会随着照相机的运动很自然地移动。如上一节所示，给定一幅带有标记平面的图像，我们能够计算出照相机的位置和姿态，使用这些信息来放置计算机图形学模型，能够正确表示它们。

PyGame和PyOpenGL

PyGame 是非常流行的游戏开发工具包，它可以非常简单地处理显示窗口、输入设备、事件，以及其他内容。 它是一个 Python 绑定的 SDL 游戏引擎。

pygame 可直接使用pip install命令安装

pip install PyGame
1

安装PyOpenGL

pip install PyOpenGL
1

直接这样安装64位系统会报错。
pip默认安装的是32位的。需要使用pip uninstall pkg把OpenGL和OpenGL_accelerate都卸掉.

自己到官网下载一下适合自己的版本：
http://www.lfd.uci.edu/~gohlke/pythonlibs/#pyopengl

OpenGL 是 OpenGL 图形编程的 Python 绑定接口。 OpenGL 可以安装在几乎所有的系统上，并且具有很好的图形性能。 OpenGL 具有跨平台性，能够在不同的操作系统之间工作。

需要注意的是， 为了使用上面两个工具包，需要在脚本的开始部分载入下面的命令：

from OpenGL.GL import *
from OpenGL.GLU import *
import pygame, pygame.image
from pygame.locals import *

1
2
3
4
5

安装后测试代码：

def drawFunc():
    glClear(GL_COLOR_BUFFER_BIT)
    # glRotatef(1, 0, 1, 0)
    glutWireTeapot(0.5)
    glFlush()

def testOPENGL():
    glutInit()
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA)
    glutInitWindowSize(400, 400)
    # 参数为b类型而不是string
    glutCreateWindow(b"First")
    glutDisplayFunc(drawFunc)
    # glutIdleFunc(drawFunc)
    glutMainLoop()
    
    return
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

输出如下：

OpenGL安装正确。

从照相机矩阵到OpenGL格式

OpenGL 使用 4× 4 的矩阵来表示变换（包括三维变换和投影）。这和我们使用的 3× 4 照相机矩阵略有差别。但是，照相机与场景的变换分成了两个矩阵，GL_PROJECTION 矩阵和 GL_MODELVIEW 矩阵。 GL_PROJECTION 矩阵处理图像成像的性质，等价于我们的内标定矩阵 K。 GL_MODELVIEW 矩阵处理物体和照相机之间的三维变换关系，对应于我们照相机矩阵中的 R 和 t 部分。一个不同之处是，假设照相机为坐标系的中心， GL_MODELVIEW 矩阵实际上包含了将物体放置在照相机前面的变换。

假设我们已经获得了标定好的照相机，即已知标定矩阵 K，下面的函数可以将照相机参数转换为 OpenGL 中的投影矩阵：

def set_projection_from_camera(K):
    """从照相机标定矩阵中获得视图"""

    glMatrixMode(GL_PROJECTION)
    glLoadIdentity()

    fx = K[0,0]
    fy = K[1,1]
    fovy = 2 * arctan(0.5*height / fy) * 180 / pi
    aspect = (width*fy) / (height * fx)

    # 定义近的和圆的裁剪平面
    near = 0.1
    far = 100.0
    # 设定透视
    gluPerspective(fovy, aspect, near, far)
    glViewport(0, 0, width, height)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

第 一 个 函 数glMatrixMode() 将工作矩阵设置为 GL_PROJECTION，接下来的命令会修改这个矩阵 。 然后， glLoadIdentity() 函数将该矩阵设置为单位矩阵，这是重置矩阵的一般操作。然后，我们根据图像的高度、照相机的焦距以及纵横比，计算出视图中的垂直场。 OpenGL 的投影同样具有近距离和远距离的裁剪平面来限制场景拍摄的深度范围。我们设置近深度为一个小的数值，使得照相机能够包含最近的物体，而远深度设置为一个大的数值。我们使用 GLU 的实用函数 gluPerspective() 来设置投影矩阵，将整个图像定义为视图部分（也就是显示的部分）。和下面的模拟视图函数相似，你可以使用 glLoadMatrixf() 函数的一个选项来定义一个完全的投影矩阵。当简单版本的标定矩阵不够好时，可以使用完全投影矩阵。模拟视图矩阵能够表示相对的旋转和平移，该变换将该物体放置在照相机前（效果是照相机在原点上）。模拟视图矩阵是个典型的 4× 4 矩阵，如下所示：
[ R t 0 1 ] \left[

\right] [R0​t1​]
R 是旋转矩阵，列向量表示 3 个坐标轴的方向， t 是平移向量。当创建模拟视图矩阵时，旋转矩阵需要包括所有的旋转（物体和坐标系的旋转），可以将单个旋转分量相乘来获得旋转矩阵。

下面的函数实现如何获得移除标定矩阵后的 3× 4 针孔照相机矩阵（将 P 和 K -1 相乘），并创建一个模拟视图：

def set_modelview_from_camera(Rt):
    """从照相机姿态中获得模拟视图矩阵"""

    glMatrixMode(GL_MODELVIEW)
    glLoadIdentity()
    # 围绕x轴将茶壶旋转90度，使z轴向上
    Rx = np.array([[1, 0, 0], [0, 0, -1], [0, 1, 0]])
    # 获得旋转的最佳逼近
    R = Rt[:, :3]
    U, S, V = np.linalg.svd(R)
    R = np.dot(U, V)
    R[0, :] = -R[0, :]  # 改变x轴的符号
    # 获得平移量
    t = Rt[:, 3]
    # 获得4*4的的模拟视图矩阵
    M = np.eye(4)
    M[:3, :3] = np.dot(R, Rx)
    M[:3, 3] = t
    # 转置并压平以获取列序数值
    M = M.T
    m = M.flatten()
    # 将模拟视图矩阵替换成新的矩阵
    glLoadMatrixf(m)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

在上面函数中，我们首先切换到 GL_MODELVIEW 矩阵，然后重置该矩阵。然后，由于需要旋转该物体（你将在下面看到），所以我们创建一个 90 度的旋转矩阵。接下来，由于估计照相机矩阵时，可能会有错误或者噪声干扰，所以我们确保照相机矩阵的旋转部分确实是个旋转矩阵。该操作使用 SVD 分解方法，旋转矩阵的最佳逼近可以通过 R=UVT 来获得。由于 OpenGL 中的坐标系和上面用到的有点不同，所以我们将 x 轴翻转。然后，我们将模拟视图矩阵 M 设置为旋转矩阵的乘积。glLoadMatrixf() 函数通过输入参数为按列排列的 16 个数值数组，来设置模拟视图。将 M 矩阵转置，然后压平并输入 glLoadMatrixf() 函数。

在图像中放置虚拟物体

我们需要做的第一件事是将图像（打算放置虚拟物体的图像）作为背景添加进来。在 OpenGL 中，该操作可以通过创建一个四边形的方式来完成，该四边形为整个视图。完成该操作最简单的方式是绘制出四边形，同时将投影和模拟试图矩阵重置，使得每一维的坐标范围在 -1 到 1 之间。

下面的函数可以载入一幅图像，然后将其转换成一个 OpenGL 纹理，并将该纹理放置在四边形上：

def draw_background(imname):
    # 载入背景图像
    bg_image = pygame.image.load(imname).convert()
    bg_data = pygame.image.tostring(bg_image, "RGBX", 1)  # 将图像转为字符串描述
    glMatrixMode(GL_MODELVIEW)  # 将当前矩阵指定为投影矩阵
    glLoadIdentity()  # 把矩阵设为单位矩阵

    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)  # 清楚颜色、深度缓冲
    glEnable(GL_TEXTURE_2D)  # 纹理映射
    glBindTexture(GL_TEXTURE_2D, glGenTextures(1))
    glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, width, height, 0, GL_RGBA, GL_UNSIGNED_BYTE, bg_data)
    glTexParameterf(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST)
    glTexParameterf(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST)
    
    # 绑定纹理
    # 创建四方形填充整个窗口
    glBegin(GL_QUADS)
    glTexCoord2f(0.0, 0.0); glVertex3f(-1.0, -1.0, -1.0)
    glTexCoord2f(1.0, 0.0); glVertex3f(1.0, -1.0, -1.0)
    glTexCoord2f(1.0, 1.0); glVertex3f(1.0, 1.0, -1.0)
    glTexCoord2f(0.0, 1.0);  glVertex3f(-1.0, 1.0, -1.0)
    glEnd()

    glDeleteTextures(1)  # 清除纹理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

该函数首先使用 PyGame 中的一些函数来载入一幅图像，将其序列化为能够在PyOpenGL 中使用的原始字符串表示。然后，重置模拟视图，清除颜色和深度缓存。接下来，绑定这个纹理，使其能够在四边形和指定插值中使用它。四边形是在每一维分别为 -1 和 1 的点上定义的。注意，纹理图像的坐标是从 0 到 1。最后，清除该纹理，避免其干扰之后准备绘制的图像。

现在已经准备好将物体放置入场景中。我们将使用“ hello world”的计算机图形学例子， Utah 茶壶这个茶壶有丰富的历史，在 GLUT 用作一个标准形状。

ef draw_teapot(size):  # 红色茶壶
    glEnable(GL_LIGHTING)
    glEnable(GL_LIGHT0)
    glEnable(GL_DEPTH_TEST)
    glClear(GL_DEPTH_BUFFER_BIT)
    # 绘制红色茶壶
    glMaterialfv(GL_FRONT, GL_AMBIENT, [0, 0, 0, 0])
    glMaterialfv(GL_FRONT, GL_DIFFUSE, [0.5, 0.0, 0.0, 0.0])
    glMaterialfv(GL_FRONT, GL_SPECULAR, [0.7, 0.6, 0.6, 0.0])
    glMaterialf(GL_FRONT, GL_SHININESS, 0.25 * 128.0)
    glutSolidTeapot(size)
1
2
3
4
5
6
7
8
9
10
11

上面的函数中，前两行激活了灯光效果和一盏灯。 灯被计为GL_LIGHT0 和GL_LIGHT1 等。在本例中，我们只使用一盏灯。 glEnable() 函数用来激活 OpenGL的一些特性。这些特性是使用大写常量来定义的。关闭特性可以使用相应的glDisable() 函数来完成。接下来，深度测试被激活，使物体按照其深度表示出来（远处的物体不能绘制在近处物体的前面），然后清理深度缓存。接下来，指定物体的物质特性，例如漫反射和镜面反射颜色。在最后一行代码中，将指定的物质特性加入到 Utah 茶壶上。

综合集成

def set_projection_from_camera(K):
    """从照相机标定矩阵中获得视图"""

    glMatrixMode(GL_PROJECTION)
    glLoadIdentity()

    fx = K[0,0]
    fy = K[1,1]
    fovy = 2 * arctan(0.5*height / fy) * 180 / pi
    aspect = (width*fy) / (height * fx)

    # 定义近的和圆的裁剪平面
    near = 0.1
    far = 100.0
    # 设定透视
    gluPerspective(fovy, aspect, near, far)
    glViewport(0, 0, width, height)

def set_modelview_from_camera(Rt):
    """从照相机姿态中获得模拟视图矩阵"""

    glMatrixMode(GL_MODELVIEW)
    glLoadIdentity()
    # 围绕x轴将茶壶旋转90度，使z轴向上
    Rx = np.array([[1, 0, 0], [0, 0, -1], [0, 1, 0]])
    # 获得旋转的最佳逼近
    R = Rt[:, :3]
    U, S, V = np.linalg.svd(R)
    R = np.dot(U, V)
    R[0, :] = -R[0, :]  # 改变x轴的符号
    # 获得平移量
    t = Rt[:, 3]
    # 获得4*4的的模拟视图矩阵
    M = np.eye(4)
    M[:3, :3] = np.dot(R, Rx)
    M[:3, 3] = t
    # 转置并压平以获取列序数值
    M = M.T
    m = M.flatten()
    # 将模拟视图矩阵替换成新的矩阵
    glLoadMatrixf(m)

def draw_background(imname):
    # 载入背景图像
    bg_image = pygame.image.load(imname).convert()
    bg_data = pygame.image.tostring(bg_image, "RGBX", 1)  # 将图像转为字符串描述
    glMatrixMode(GL_MODELVIEW)  # 将当前矩阵指定为投影矩阵
    glLoadIdentity()  # 把矩阵设为单位矩阵

    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)  # 清楚颜色、深度缓冲
    glEnable(GL_TEXTURE_2D)  # 纹理映射
    glBindTexture(GL_TEXTURE_2D, glGenTextures(1))
    glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, width, height, 0, GL_RGBA, GL_UNSIGNED_BYTE, bg_data)
    glTexParameterf(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST)
    glTexParameterf(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST)
    # 绑定纹理
    glBegin(GL_QUADS)
    glTexCoord2f(0.0, 0.0); glVertex3f(-1.0, -1.0, -1.0)
    glTexCoord2f(1.0, 0.0); glVertex3f(1.0, -1.0, -1.0)
    glTexCoord2f(1.0, 1.0); glVertex3f(1.0, 1.0, -1.0)
    glTexCoord2f(0.0, 1.0); glVertex3f(-1.0, 1.0, -1.0)
    glEnd()
    glDeleteTextures(1)  # 清除纹理

def draw_teapot(size):  # 红色茶壶
    glEnable(GL_LIGHTING)
    glEnable(GL_LIGHT0)
    glEnable(GL_DEPTH_TEST)
    glClear(GL_DEPTH_BUFFER_BIT)
    # 绘制红色茶壶
    glMaterialfv(GL_FRONT, GL_AMBIENT, [0, 0, 0, 0])
    glMaterialfv(GL_FRONT, GL_DIFFUSE, [0.5, 0.0, 0.0, 0.0])
    glMaterialfv(GL_FRONT, GL_SPECULAR, [0.7, 0.6, 0.6, 0.0])
    glMaterialf(GL_FRONT, GL_SHININESS, 0.25 * 128.0)
    # 该命令产生一个相对大小为 size 的茶壶模型。
    # glutWireTeapot(size)
    glutSolidTeapot(size)

def drawFunc(size):  # 白色茶壶
    glRotatef(0.5, 5, 5, 0)  # (角度,x,y,z)
    glutWireTeapot(size)
    # 刷新显示
    glFlush()

width, height = 1000, 747


def setup():  # 设置窗口和pygame环境
    pygame.init()
    pygame.display.set_mode((width, height), OPENGL | DOUBLEBUF)
    pygame.display.set_caption("OpenGL AR demo")
    
    return 

def comprehensiveIntegration():
    # 计算特征
    harris.process_image('picture/book_frontal.jpg', 'im0.sift')
    l0, d0 = harris.read_features_from_file('im0.sift')

    harris.process_image('picture/book_perspective.JPG','im1.sift')
    l1, d1 = harris.read_features_from_file('im1.sift')

    # 匹配特征，计算单应性矩阵
    matches = harris.match_twosided(d0, d1)
    ndx = matches.nonzero()[0]
    fp = homography.make_homog(l0[ndx, :2].T)
    ndx2 = [int(matches[i]) for i in ndx]
    tp = homography.make_homog(l1[ndx2, :2].T)

    model = homography.RansacModel()
    H, inliers = homography.H_from_ransac(fp, tp, model)

    # 计算照相机标定矩阵
    K = my_calibration((747, 1000))
    # 位于边长为0.2，z=0平面上的三维点
    box = cube_points([0, 0, 0.1], 0.1)

    # 投影第一幅图下个上底部的正方形
    cam1 = camera.Camera(hstack((K, dot(K, array([[0], [0], [-1]])))))
    # 底部正方形上的点
    box_cam1 = cam1.project(homography.make_homog(box[:, :5]))

    # 使用H将点变换到第二幅图像中
    box_trans = homography.normalize(dot(H, box_cam1))

    # 从cam1和H中计算第二个照相机矩阵
    cam2 = camera.Camera(dot(H, cam1.P))
    A = dot(linalg.inv(K), cam2.P[:, :3])
    A = array([A[:, 0], A[:, 1], cross(A[:, 0], A[:, 1])]).T
    cam2.P[:, :3] = dot(K, A)
    # 使用第二个照相机矩阵投影
    box_cam2 = cam2.project(homography.make_homog(box))

    Rt = dot(linalg.inv(K), cam2.P)

    setup()       
    draw_background(r"C:/hqq/document/python/computervision/ch04/picture/book_perspective.bmp")
    set_projection_from_camera(K)
    set_modelview_from_camera(Rt)
    
    # draw_teapot(0.05)  # 显示红色茶壶
    drawFunc(0.05)  # 显示白色空心茶壶
    pygame.display.flip()
    
    while True:
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                sys.exit()

    return

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152

代码运行结果出不来，只是黑屏一闪而过。
目前问题定位到了：

 glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, width, height, 0, GL_RGBA, GL_UNSIGNED_BYTE, bg_data)
1

这句，程序顺序执行下来的时候，到这里会卡住，不在继续执行。问题是在这，但我看之前的做出结果的代码，这里是一样的。所以怀疑是不是系统问题。

后面再处理这个问题。

输出结果如下：

改出来了，一共调整两个地方，一个是修改

width, height = 300, 400
1

另外一个地方是在调用茶壶的地方加上初始化函数。

改完就欧克了！！！

4.5 小结

本章引入了照相机矩阵，由三维点 X 投影到图像点x 可以由式$\lambda \mathbf{x}=\mathbf{PX}$表示，我们得到了照相机矩阵P。之后将照相机矩阵分解为$\mathbf{P}=K[\mathbf{R}\mid \mathbf{t}]$。内标定矩阵 K ，R 是描述照相机方向的旋转矩阵，t 是描述照相机中心位置的三维平移向量。再利用一些变换和替换，将问题引到了标定矩阵上。之后是利用推导得到的公式，利用采到的图片去计算出该照相机的内参数，就是做照相机标定。之后根据前一章的单应性矩阵，与标定的照相机参数，可以推导出照相机位置。之后更具推到出的照相机位置将一些三维图像与我们的图片进行结合。

本章大致过程是这样的。但是代码没调出来 。调出来了！！！！
还是附上吧！
链接：https://pan.baidu.com/s/1LFA14y7BtoNTJp3QG4H_uA?pwd=31zl
提取码：31zl
链接：https://pan.baidu.com/s/1WRUgJG9JN3DTGVTVwD9CCw?pwd=yw1d
提取码：yw1d