-
52、GNT:Is Attention All NeRF Needs?
简介
主页:https://vita-group.github.io/GNT/

与之前通过反转手工渲染方程来优化每个场景隐式表示的NeRF工作不同,GNT通过封装两个基于transformer的阶段,实现了可泛化的神经场景表示和渲染GNT的第一个阶段,称为view transformer,利用多视图几何作为基于注意力的场景表示的归纳偏差,并通过聚合相邻视图上的极线信息来预测坐标对齐的特征
GNT的第二阶段,称为ray transformer,通过射线行进渲染新视图,并使用注意力机制直接解码采样点特征序列
体绘制最初被提议处理半透明和非表面材料。它缺乏固体表面、反射率、表面间散射等的光学建模。这意味着辐射场和体绘制并不是一个通用的成像模型,这可能也限制了nerf的泛化能力。
贡献点
- 提出了一个纯粹基于变压器的NeRF架构,称为GNT,通过将坐标网络和体积渲染器统一到一个两级变压器中,实现了更有表现力和更通用的场景表示和渲染,能够在跨实例训练时泛化到不可见的场景。
- 为了获得更有表现力的体积表示,GNT采用view transformer聚合符合极线几何的多视图图像特征,从而推断出坐标对齐的特征。为了学习更通用的基于光线的渲染,GNT利用ray transform来预测光线颜色。这两个部分组成了一个转换器,完全依靠注意机制呈现新奇的视图,并固有地学习深度和闭塞意识。
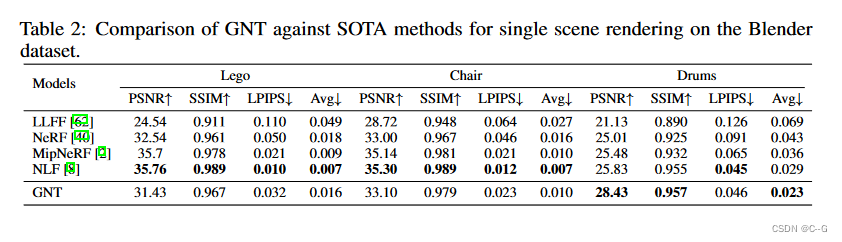
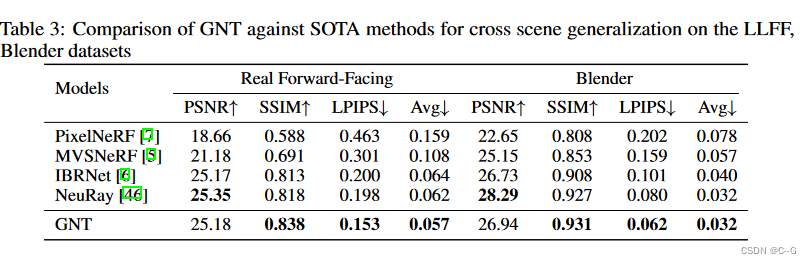
- 经验证明,在复杂场景中,GNT显著提高了现有nerf(单场景)的PSNR,最高可达1.3 dB。在跨场景泛化场景中,GNT通过超越其他基线达到最先进的感知度量得分~20%↓lpip和~12%↑SSIM
实现流程
相关工作
Self-Attention and Transformer
multihead Self-Attention (MHA)是转换器的主要组成部分,它根据成对计算的分数在标记之间交换信息,该分数表示对上下文子集的关注
形式上,设 X ∈ R N × d X∈R^{N×d} X∈RN×d表示具有 N个d 维标记的顺序数据。自注意层将特征矩阵转换如下
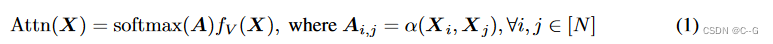
A ∈ R N × N A∈R^{N×N} A∈RN×N为注意矩阵, softmax(·) 运算对注意矩阵行进行了明智的归一化,α(·)表示成对关系函数,最常用的关系映射是点积 α ( X i , X j ) = f Q ( X i ) T f K ( X j ) / y α(X_i, X_j)= f_Q(X_i)^T f_K (X_j)/ y α(Xi,Xj)=fQ(Xi)TfK(Xj)/y,其中 f Q ( ⋅ )、 f K ( ⋅ )、 f V ( ⋅ ) f_Q(·)、f_K (·)、f_V (·) fQ(⋅)、fK(⋅)、fV(⋅) 称为 query 、key 和 value 映射函数。在标准 transformer 中,它们被选为全连接层,自我注意的功能可以看作是一个聚合运算符,它根据一个令牌之间的注意值将信息从一个令牌传递到另一个令牌,Multi-Head Self-Attention (MHA)设置一组自注意块,并采用线性层将其投射到输出空间上
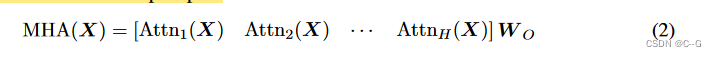
在MHA块之后,一个标准的 transformer 层还采用前馈网络(FFN)进行逐点特征转换,以及跳越连接和层归一化来稳定训练。整个 transformer 块可表述为:
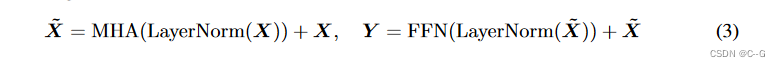
Neural Radiance Field
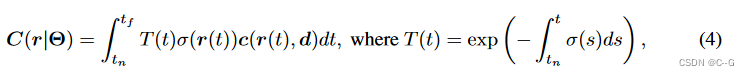
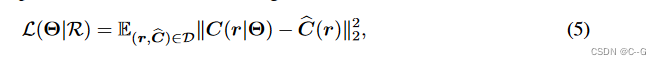
Make Attention All NeRF Needs
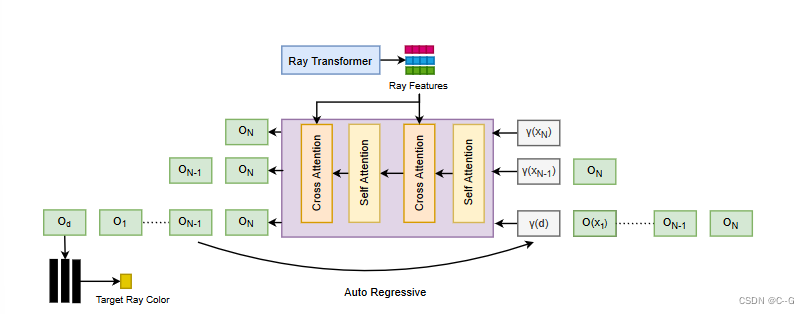
GNT概述- 为给定的目标视图识别源视图
- 使用可训练的U-Net类模型提取极线点的特征
- 针对目标视图中的每条射线,通过聚合视图特征(view Transformer)和沿射线的跨点(ray
Transformer),采样点并直接预测目标像素的颜色。
给定一组N个输入视图,已知摄像机参数 { ( I i ∈ R H × W × 3 , p i ∈ R 3 × 4 ) } i = 1 N \{(I_i∈R^{H×W ×3}, p_i∈R^{3×4})\}^N_{i=1} {(Ii∈RH×W×3,pi∈R3×4)}i=1N,目标是从任意角度合成新颖的视图,遵循跨场景通用NeRF的设计,该方法可分为两个阶段:1)在特征空间中动态构建源视图的三维表示;2)以指定角度重新渲染特征场,合成新的视图
对于第一阶段,使用视图转换器聚合源视图的坐标对齐特征。为了加强多视图几何,在注意机制中加入极界约束的归纳偏差。在获得射线上每个点的特征表示后,GNT利用射线转换器沿射线组合点向特征,形成射线颜色。整个管道是纯粹基于注意力的,可以端到端进行训练
Epipolar Geometry Constrained Scene Representation
Multi-View Feature Aggregation
GNT以前馈方案构建亮度场,直接将多视图图像编码到3D特征空间,并解码为颜色密度场,没有将3D特征转化为物理变量(如颜色和密度),而是隐式地将3D场景表示为坐标对齐的特征场 F : ( x , θ ) → F ∈ R d F: (x, θ)→F∈R^d F:(x,θ)→F∈Rd,其中 d 为潜在空间的维数。制定前馈场景表示如下:

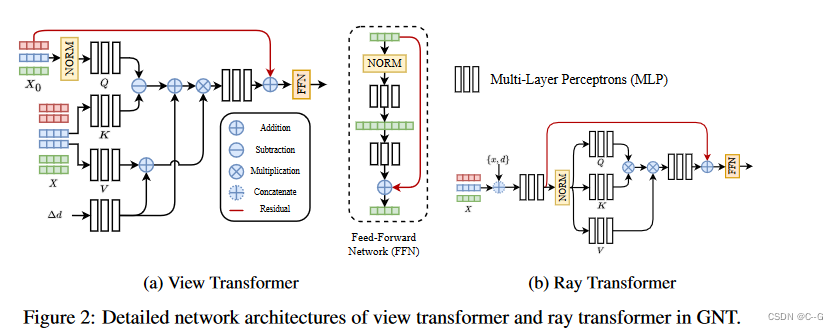
其中 V(·) 是一个对输入图像排列不变的函数,将不同的视图 { I i , ⋅ ⋅ ⋅ , I N I_i,···,I_N Ii,⋅⋅⋅,IN} 聚合为一个坐标对齐的特征域,并提取特定位置的特征, transformer 可以作为一个通用集聚合函数.但是,直接插入全局关注源图像中的每个像素的注意机制是内存禁止的,而且缺乏多视图几何先验,为此,引入极线几何作为一种归纳偏差,它限制每个像素只关注位于相邻视图对应极线上的像素,将这种基于交极几何的交叉视图聚合转换器 V(·)命名为 view transformer
首先,通过共享的基于U-Net的卷积神经网络从每张图像中提取特征映射 F i = U N e t ( I i ) ∈ R H × W × d F_i = UNet(I_i)∈R^{H×W ×d} Fi=UNet(Ii)∈RH×W×d。为了得到 x 位置的特征表示,首先将 x 投影到每个源图像上,并在图像平面上插值特征向量。然后,采用一个 transformer 来合并所有的特征向量
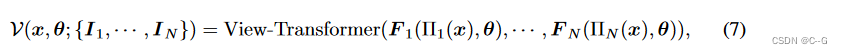
其中 View-Transformer(·)是 式3(transformer块) 的多层叠加。 π i ( x ) = [ x / z y / z ] T 和 [ x y z ] T = P i [ x 1 ] T \pi_i(x) = [x/z\ y/z]^T 和 [x\ y\ z]^T = P_i [x\ 1]^T πi(x)=[x/z y/z]T和[x y z]T=Pi[x 1]T 将 3 D点 x ∈ R 3 x∈R^3 x∈R3 投影到第 i 个像平面上。 F i ( x ′ , θ ) ∈ R d F_i(x', θ)∈R^d Fi(x′,θ)∈Rd 通过特征网格上的双线性插值计算 x ′ ∈ R 2 x'∈R^2 x′∈R2 位置的特征向量。还将提取的特征向量与点坐标 γ(x)、观测方向γ(θ) 和 源视图相对于目标视图的相对方向 ∆ d i = γ ( x − o i ) ∆d_i = γ(x−o_i) ∆di=γ(x−oi) 连接,其中 o i o_i oi 为第 i 个摄像机的原点,γ(·) 表示位置编码函数。Memory-Efficient Cross-View Attention
每对输入之间的计算注意力具有 O ( n 2 ) O(n^2) O(n2) 的内存复杂度,当同时采样数千个点时,这是计算上的禁忌。然而, 注意到视图转换器只需要读出一个令牌作为所有视图的融合结果。因此, 建议在查询序列中只放置一个读出令牌 X 0 ∈ R d X_0∈R^d X0∈Rd,并让它迭代地总结来自其他数据点的特征。这将每层的复杂度降低到 O(N)。 将读出令牌初始化为所有输入的元素级 max-pooling: X 0 = m a x ( F 1 ( π 1 ( x ) , θ ) , ⋅ ⋅ ⋅ , F N ( π N ( x ) , θ ) ) X_0 = max(F_1 (\pi_1(x), θ),···,F_N (\pi_N (x), θ)) X0=max(F1(π1(x),θ),⋅⋅⋅,FN(πN(x),θ))。没有采用标准的点积注意,而是选择减法运算作为关系函数。减法注意已被证明在位置和几何关系推理中更有效。与将特征维度分解为标量的点积相比,减法注意对值矩阵的每个通道计算不同的注意得分,增加了特征交互的多样性。此外,用 ∆ d i N = 1 {∆d}^N_i=1 ∆diN=1 来增加注意图和值矩阵,以提供相对的空间上下文。技术上,利用线性层 W P W_P WP 将 ∆ d i ∆d_i ∆di 提升到隐藏维度。更具体地说,视图转换器中采用的修改后的注意可以表述为:
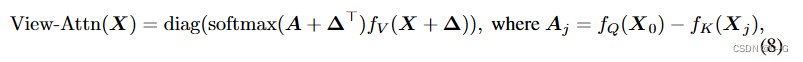
其中 A j ∈ R d A_j∈R^d Aj∈Rd 表示 A 的第 j 列, ∆ = [ ∆ d 1 ⋅ ⋅ ⋅ ∆ d N ] T W P ∈ R N × d , f Q 、 f K 和 f V ∆=[∆d_1···∆d_N]^T W_P∈R^{N×d}, f_Q、f_K和f_V ∆=[∆d1⋅⋅⋅∆dN]TWP∈RN×d,fQ、fK和fV 由MLP参数化。我们注意到,通过应用 diag(·), 读取了更新后的查询令牌 X 0 X_0 X0。

Discussion on Occlusion Awareness
从概念上讲,view transformer 试图找到被查询点与源视图之间的对应关系。习得的注意力相当于源视图上的像素是3D空间中同一点的图像的可能性得分,也就是说,在目标点和像素之间没有点。NeuRay 利用来自 MVSNet 的成本量来预测每像素可见性,并表明引入遮挡信息有利于泛化 NeRF 中的多视图聚合。考虑到之前在多视图立体(MVS)方面的研究 ,单纯依靠极线几何约束注意力可以自动学习如何推断遮挡,而不是显式地回归可见性。在视图转换器中,U-Net为转换器提供多尺度特征,attention block 作为匹配算法,从相邻视图中选择像素点,使视图一致性最大化
Attention Driven Volumetric Rendering
体渲染 被认为是NeRF成功的关键,它模拟了光在辐射场中的传输和遮挡。可泛化的NeRF 也继承了NeRF的渲染功能,并显式地将中间3D潜在表示解码为颜色密度场。然而,体绘制在建模尖锐的表面 和复杂的干涉模式(如镜面反射 、折射和半透明 )方面仍然存在困难。尽管已有文献对物理成像建模进行了研究,但都不能统一一个适用于所有场景的渲染方程。这促使我们用一个数据驱动的渲染器来取代手工制作的渲染函数,该渲染器学会根据特定的相机姿势将3D特征场投影到2D图像上。
Ray Feature Aggregation
首先遵循基于射线的渲染管道。也就是说,首先从摄像机原点投射一条射线 r = (o, d),穿过要渲染的像素,然后沿着射线随机采样 M个点 { x i = o + t i d } i = 1 M \{ x_i = o + t_id\}^M_{i=1} {xi=o+tid}i=1M,计算 Eq. 4 的数值估计。将公式4的数值估计重写为加权求和
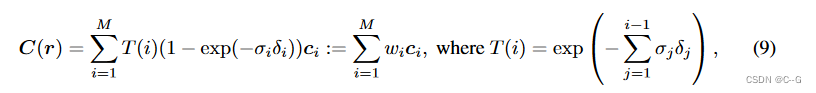
w i = T ( i ) ( 1 − e x p ( − σ i δ i ) ) w_i = T (i)(1−exp(−σ_iδ_i)) wi=T(i)(1−exp(−σiδi))。可以看到,体绘制是所有按点输出的加权聚合,其中权重依赖于遮挡建模的其他点。注意到,这一过程与注意力的计算范式具有内在的相似性,其中标记特征对应 c i c_i ci,注意分数对应 w i w_i wi。因此,可以用一个 ray transformer 来推广式9。根据视图变换,可以为每个采样点 x i x_i xi 计算一个特征表示 f i = f ( x i , θ ) ∈ R d f_i = f (x_i, θ)∈R^d fi=f(xi,θ)∈Rd。此外,还将空间位置 γ(x) 和视图方向 γ(θ) 加入到 f i f_i fi 中。我们将 { f 1 , ⋅ ⋅ ⋅ , f M f_1,···,f_M f1,⋅⋅⋅,fM} 序列输入到 ray transformer 中,得到渲染的射线颜色,对所有预测标记进行均值池化,并通过 MLP 将池化后的特征向量映射到 RGB。整个过程可以表述为:
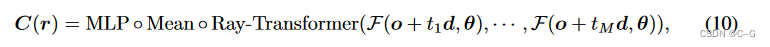
其中 t i ∼ U [ t n + ( i − 1 ) ( t f − t n ) / M , t n + i ( t f − t n ) / M ] t_i∼U [t_n + (i−1)(t_f−t_n)/M, t_n + i(t_f−t_n)/M] ti∼U[tn+(i−1)(tf−tn)/M,tn+i(tf−tn)/M] 。与 view transformer 不同的是,在 ray transformer 中采用了标准的点积注意,这鼓励更多的跨点交互,为准确的占用和遮挡预测提供足够的上下文信息(这类似于平面扫描立体方法,考虑在所有假设平面上匹配分数)。我们认为, ray transformer 可以自动学习注意分布来控制重建曲面的锐度,并从源图像中提取照明和材料感知特征来制作理想的照明效果。

Discussion on Depth Cuing
ray transformer 根据注意值迭代聚合特征。这个注意值可以看作是每个点形成图像的重要性,它反映了通过点对点交互推理出的可见性和遮挡性。因此,可以将每个点的平均注意力得分解释为公式9中的累积权重 w i w_i wi。从这个意义上说,可以通过将行进距离 t i t_i ti 与注意值取平均值来从注意图中推断出深度图。这意味着 ray transformer 在特征空间和注意地图上学习几何感知的3D语义,这有助于它在场景中很好地泛化。NLFv提出了一个类似的两阶段渲染 transformer,但它首先提取极线上的特征,然后聚合极线特征来获得像素颜色。这种策略可能无法推广,因为极线特征之间缺乏交流,因此不能推导出几何接地语义。
Implementation Details
Source and Target view sampling
首先选择一个目标视图,然后识别一个由 k × N 个邻近视图组成的池,从池中随机抽取 N 个视图作为源视图,从而构造一个源视图和目标视图的训练对。该采样策略在训练过程中模拟了不同的视图密度,因此有助于网络更好地泛化。在训练过程中,k和N 的值分别从 [1,3] 和 [8,12] 中随机均匀采样。
Network Architecture
为了从源视图中提取特征使用一个带有 ResNet 编码器的类似 U-Net 的体系结构,然后是两个上采样层作为解码器。每个 view transformer 包含一个单头交叉注意层,而 ray transformer 包含一个具有四个头的多头自注意层。这些注意层的输出被传递到具有整流线性单元(RELU)激活和 256隐藏维的相应前馈块上。在每一层的预规范化输入(LayerNorm)和输出之间应用残差连接。对于我们所有的单场景实验, 交替地堆叠4个视图和射线转换块,而 更大的泛化实验使用8个块。所有transformer (view和ray)的尺寸都是64,使用傅立叶分量将低维坐标转换为高维表示,其中频率的数量在我们所有的实验中都被选择为10。派生的视图和位置嵌入都是63维。
Training / Inference Details
使用Adam优化器在多视角姿态图像数据集上对特征提取网络和GNT进行端到端训练,以最小化预测和真实RGB像素值之间的均方误差。特征提取网络和GNT的基本学习率分别为 1 0 − 3 和 5 × 1 0 − 4 10^{−3}和5 × 10^{−4} 10−3和5×10−4,在训练步骤中呈指数衰减。在我们所有的实验中,训练25万步,每次迭代采样2048条射线。与大多数NeRF方法不同的是,我们不使用单独的粗、细网络,并且在所有实验中只对每条射线采样64个粗点(除非另有说明)。
效果


-
相关阅读:
构建React TodoList应用:管理你的任务清单
jvmJava虚拟机
无聊话语罢了
算数练习——模拟
三极管及继电器的使用(单片机如何控制灯泡等大型电器)
Python PDF文件合并,提取
各种语言如何连接到 OceanBase
C++函数如何具有多个返回值?
基础设施即代码(IAC),Zalando Postgres Operator UI 入门
【论文阅读|深读】Role2Vec:Role-Based Graph Embeddings
- 原文地址:https://blog.csdn.net/weixin_50973728/article/details/127040891