-
一文搞懂序列密码
1. 基本概念
序列密码,又称为流密码,属于对称密码体制,它一次只对明文消息的单个字符(通常是二进制位)进行加解密变换,具有实现简单、速度快、错误传播少等特点,是世界各国的军事和外交等领域中使用的主要密码体制之一。
序列密码的起源可追溯到Vernam密码算法,由美国电话电报公司的G.W.Vernam于1917年发明。若Vernam体制中的密钥序列是随机序列时,则为“一次一密”密码体制(one-time-pad),理论上是不可破译的。由于随机密钥序列的产生、分发及管理等方面存在一定的困难,Vernam体制在当时未得到广泛应用。随着微电子技术和数学理论的发展和完善,基于伪随机序列的序列密码得到了长足的发展和应用。
1.1 定义
在序列密码中,将明文消息按一定长度(长度较小)分组,对各组用相关但不同的密钥逐位加密产生相应的密文,相同的明文分组会因在明文序列中的位置不同而对应于不同的密文分组,接收者用相同的密钥序列对密文序列逐位解密恢复出明文。
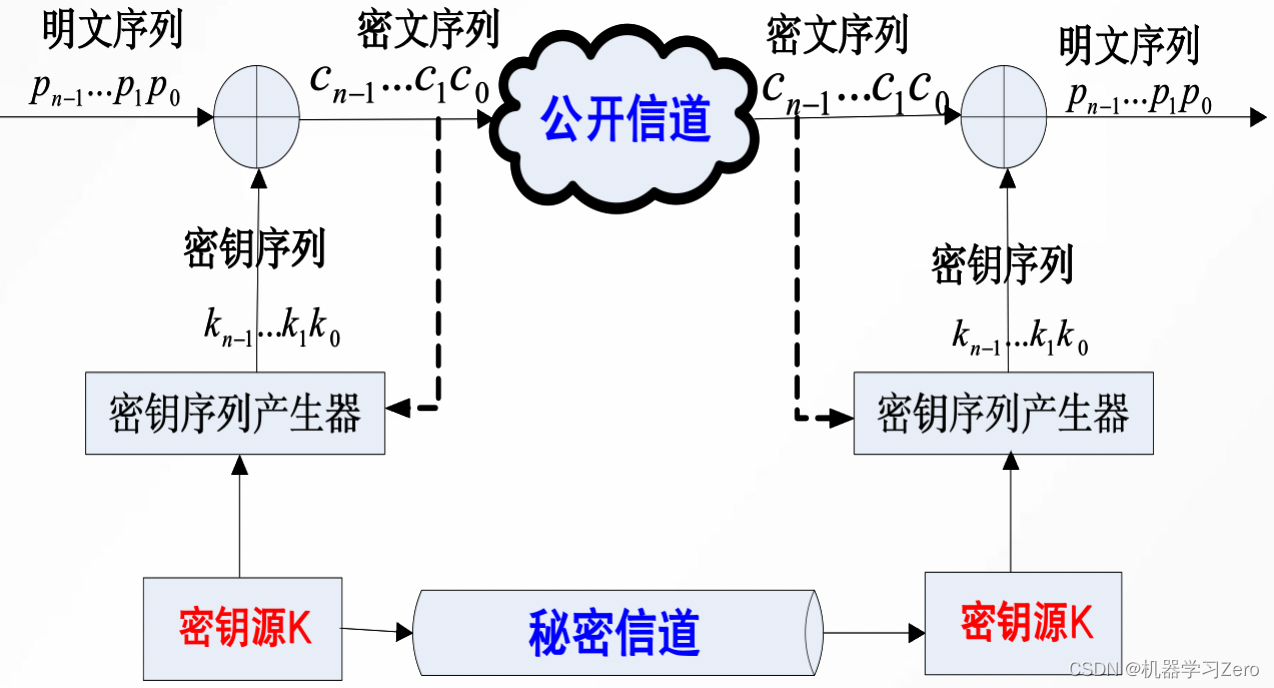
令明文序列 p = p n − 1 . . . p 1 p 0 p=p_{n-1}...p_1p_0 p=pn−1...p1p0密钥序列 k = k n − 1 . . . k 1 k 0 k=k_{n-1}...k_1k_0 k=kn−1...k1k0
密文序列 c = c n − 1 . . . c 1 c 0 = E k n − 1 ( p n − 1 ) . . . E k 1 ( p 1 ) E k 0 ( p 0 ) c=c_{n-1}...c_1c_0=E_{k_{n-1}}(p_{n-1})...E_{k_1}(p_1)E_{k_0}(p_0) c=cn−1...c1c0=Ekn−1(pn−1)...Ek1(p1)Ek0(p0)
若 c i = E k i ( p i ) = p i ⊕ k i c_i=E_{k_i}(p_i)=p_i\oplus k_i ci=Eki(pi)=pi⊕ki则称此类为加法序列密码。序列密码一般分为:
- 同步序列密码:密钥序列的产生需要收发双方进行同步,密钥序列的产生完全独立于明文消息和密文消息
- 自同步序列密码:密钥序列的产生是密钥及固定大小的以往密文位的函数
1.2 基本原理
序列密码的加解密只是简单的模二加运算,其安全强度主要依赖于密钥序列的随机性。密钥序列产生器(KG,Keystram Generator)的要求如下:
- 种子密钥 K K K的长度足够大,一般应在128位以上
- 生成的密钥序列 k i {k_i} ki具有极大周期
- k i {k_i} ki具有均匀的 n n n-元分布,即在一个周期环上,某特定形式的 n n n-长bit串与其求反,两者出现的频数大抵相当(例如,均匀的游程分布)
- 利用统计方法由 k i {k_i} ki提取关于KG结构或K的信息在计算上不可行
- 混乱性,即 k i {k_i} ki的每一bit均与K的大多数bit有关
- 扩散性,即 K K K任一bit的改变要引起 k i {k_i} ki在全貌上的变化
- 密钥序列 k i {k_i} ki不可预测,密文及相应的明文的部分信息,不能确定整个 k i {k_i} ki
根据Rainer Rueppel的理论,密钥序列产生器的内部框可分为
- 驱动部分:产生控生成器的状态序列,并控制生成器的周期和统计特性。一般利用线性反馈移位寄存器(LSFR,Linear Feedback Shift Register),如利用最长周期或 m m m序列产生器实现。
- 组合部分:组合部分对驱动部分的各个输出序列进行非线性组合,控制和提高产生器输出序列的统计特性、线性复杂度和不可预测性
1.3 序列密码的特点
- 安全强度取决于密钥序列的随机性和不可预测性
- 密钥分配困难
- 能较好的隐藏明文的统计特性
- 实时性好、加解密速度快、易实现
分组密码和序列密码都属于对称密码,但具有较大不同:
-
分组密码
- 把明文分成相对比较大的块,对于每块使用相同的加密函数进行处理,(纯)分组密码是无记忆的
- 算法关键在于加解密算法,使明文和密文之间关联在密钥的控制下尽可能复杂
-
序列密码
- 明文长度可小到1bit,序列密码是有记忆的,又被称作状态密码
- 算法关键在于密钥序列产生器,使生成的密钥序列具有尽可能高的不可预测性。
但序列密码和分组密码的区别也不是绝对的,如果把分组密码增加少量的记忆模块(如分组密码的CFB模式或OFB模式)就形成了一种序列密码。
2 线性反馈移位寄存器
2.1 定义
反馈移位寄存器(FSR,Feedback Shift Register)一般由移位寄存器和**反馈函数(Feedback Function)**组成。
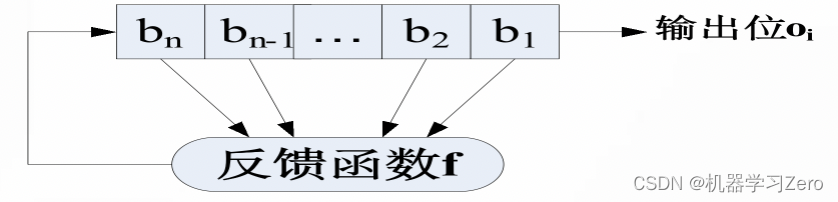
移位寄存器是由位组成的序列,其长度用位表示,每次移位寄存器中所有位右移一位,最左端的位根据寄存器中某些位计算得到,由寄存器某些位计算最左端位的部分被称为反馈函数,最右端一个寄存器移出的值是输出位。移位寄存器的周期是指输出序列从开始到重复时的长度。最简单的反馈移位寄存器是线性反馈移位寄存器(LFSR,Linear Feedback Shift Register)。
反馈函数是寄存器中某些位简单异或,这些位叫做抽头序列(Tap Sequence),有时也叫 Fibonacci 配置(Fibonacci Configuration)。举例:
一个 3 3 3级反馈移位寄存器,反馈函数 f ( x ) = b 2 ⊕ b 3 f(x) = b_2 \oplus b_3 f(x)=b2⊕b3,初态为 100 100 100,输出序列生成过程如下(周期长度为3):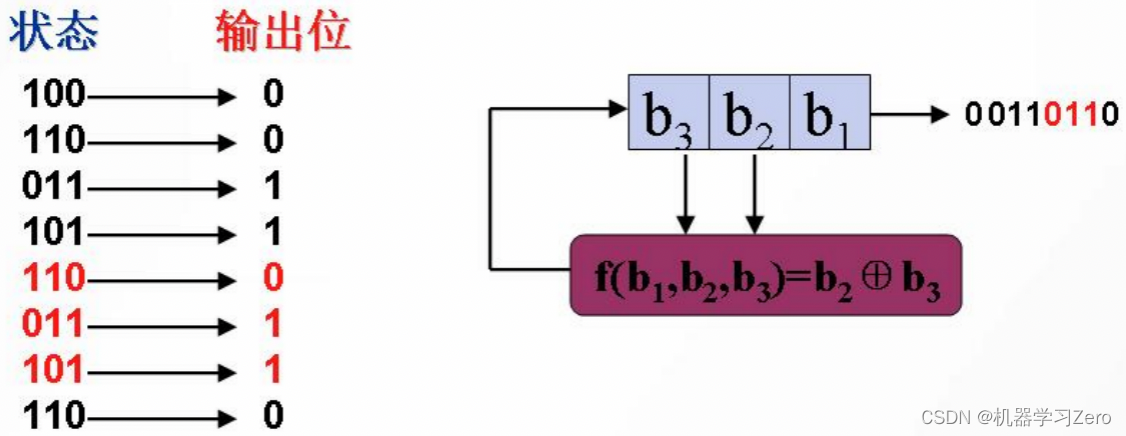
2.2 m m m序列
(1)定义
线性反馈移位寄存器输出序列的性质完全由其反馈函数决定,一个 n n n位LSFR能够处于 2 n − 1 2^{n}-1 2n−1个内部状态中的一个,即理论上, n n n位LFSR在重复之前能够产生 2 n − 1 2^{n}-1 2n−1位长的伪随机序列(是 2 n − 1 2^{n}-1 2n−1而不是 2 n 2^{n} 2n是因为全0的状态将使LFSR无止尽地输出0序列)。只要选择合适的反馈函数便可使序列的周期达到最大值 2 n − 1 2^{n}-1 2n−1,即只有具有一定抽头序列的LFSR才能循环地遍历所有 2 n − 1 2^{n}-1 2n−1个内部状态,这个输出序列被称为** m m m序列**。
为了使LFSR成为最大周期LFSR,由抽头序列加上常数1形成的多项式必须是本原多项式,多项式的阶即移位寄存器的长度。
举例: 本原多项式 p ( x ) = ( 1 + x 3 + x 4 ) p(x) = (1+x^3+x^4) p(x)=(1+x3+x4)

该序列游程总数为8,分别为 1 , 00 , 11 , 0 , 1 , 0 , 1111 , 000 1,00,11,0,1,0,1111,000 1,00,11,0,1,0,1111,000。其中,长度为 2 2 2的游程占一半,长度为 2 2 2的游程占四分之一,长度为 4 4 4的游程和长度为 3 3 3的游程均为1个。(2) m m m序列的破译
m m m序列本身是适宜的伪随机序列生成器,但在已知明文攻击下,假设破译者已知 2 n 2n 2n位明密文对 M = { m 1 , m 2 , . . . , m 2 n } M=\{m_1,m_2,...,m_{2n}\} M={m1,m2,...,m2n}, C = { c 1 , c 2 , . . . , c 2 n } C=\{c_1,c_2,...,c_{2n}\} C={c1,c2,...,c2n},则可确定一段 2 n 2n 2n位长的密钥序列 K = { k 1 , k 2 , … , k 2 n } K=\{k_1,k_2,…,k_{2n}\} K={k1,k2,…,k2n}(因为 k i = m i ㊉ c i k_i = m_i㊉c_i ki=mi㊉ci),由此可以完全确定出反馈多项式的系数,从而可确定该线性反馈移位寄存器连续的 n + 1 n+1 n+1个状态,也就能够得到余下的密钥序列。
2.3 带进位的反馈移位寄存器
带进位的反馈移位寄存器,又称FCSR(Feedback with Carry Shift Register),它与LFSR类似,都有一个移位寄存器和一个反馈函数,不同之处在于FCSR有一个进位寄存器。它不是把抽头序列中所有的位异或,是把所有的位相加,并与进位寄存器的值相加,将结果模2可得到 b n b_n bn的新值,将结果除2就得到进位寄存器新的值。
3. 非线性序列
为使密钥流生成器输出的二元序列尽可能复杂,应保证其周期尽可能大、线性复杂度和不可预测性尽可能高,因此常用多个LFSR来构造二元序列。LSFR作为驱动源,输出序列推动一个非线性函数产生非线性序列。
3.1 Geffe发生器
Geffe密钥序列发生器使用了3个LFSR以非线性方式组合而成,2个LFSR作为复合器的输入,第3个LFSR控制复合器的输出。
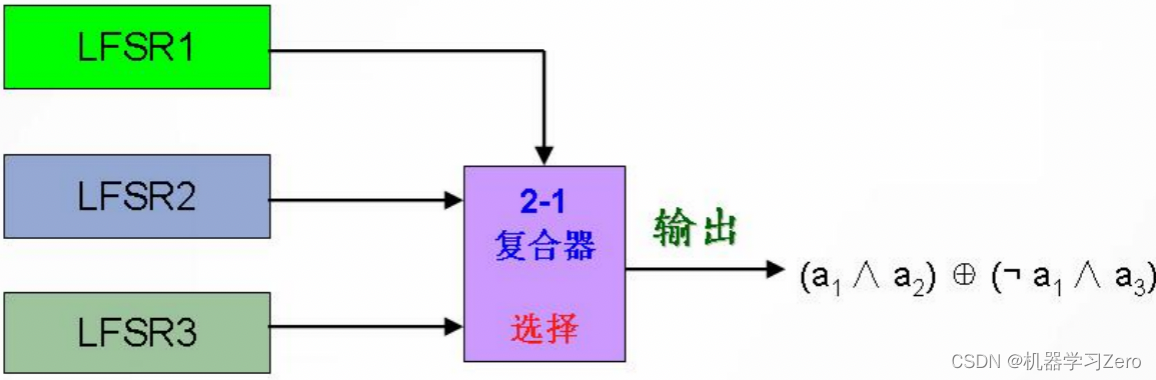
若 a 1 a_1 a1、 a 2 a_2 a2、 a 3 a_3 a3是3个LFSR的输出,则Geffe发生器输出为: b = ( a 1 ∧ a 2 ) ⊕ ( ¬ a 1 ∧ a з ) = ( a 1 ∧ a 2 ) ⊕ ( a 1 ∧ a 3 ) ⊕ a 3 b=(a_1 \wedge a_2)\oplus(\lnot a_1 \wedge a_з)=(a_1 \wedge a_2)\oplus(a_1 \wedge a_3)\oplus a_3 b=(a1∧a2)⊕(¬a1∧aз)=(a1∧a2)⊕(a1∧a3)⊕a3Geffe发生器的周期是3个LFSR的周期的最小公倍数。假设3个本原反馈多项式的阶数 n i ( i = 1 , 2 , 3 ) n_i(i=1,2,3) ni(i=1,2,3)互素,那么这个发生器的周期是3个LSFR周期之积:
( 2 n 1 − 1 ) ( 2 n 2 − 1 ) ( 2 n 3 − 1 ) (2^{n_1}-1)(2^{n_2}-1)(2^{n_3}-1) (2n1−1)(2n2−1)(2n3−1)Geffe序列的周期实现了极大化,且0与1之间的分布大体是平衡的,但实质并不能抵抗相关攻击。发生器的输出与LFSR-2的输出有75%是相同的,因此,如果已知反馈抽头,便能猜出LFSR-2的初值和寄存器所产生的输出序列。有了这种相关性,密钥序列发生器很容易被破译。3.2 J-K触发器
J-K触发器两个输入端分布用J和K表示,
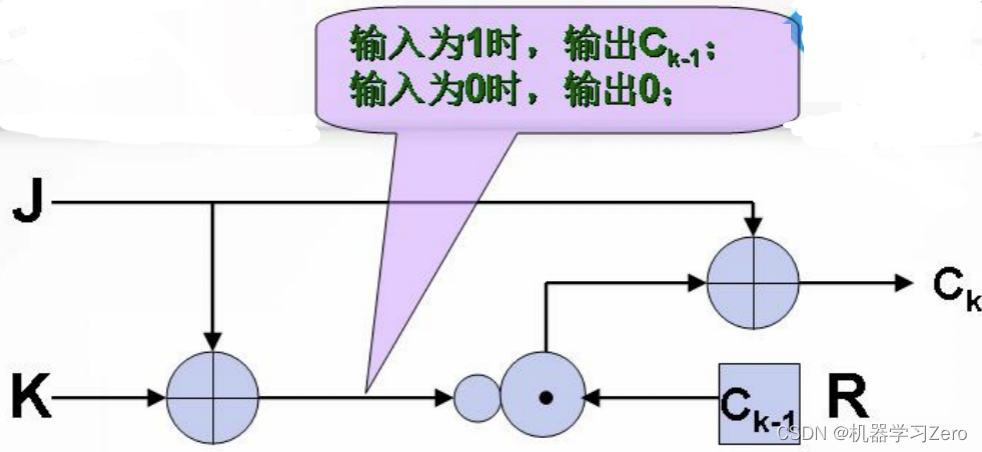
输出 c k c_k ck不仅依赖于输入,还依赖于前一位输出 c k − 1 c_{k-1} ck−1,即 c k = ( x 1 + x 2 ) − 1 c k − 1 + x 1 c_k = (x_1 + x_2)^{-1}c_{k-1}+x_1 ck=(x1+x2)−1ck−1+x1其中,$ x_1,x_2 分别表示 J 和 K 端的输入, 分别表示J和K端的输入, 分别表示J和K端的输入, (x_1 + x_2)^{-1}$表示 ( x 1 + x 2 ) (x_1 + x_2) (x1+x2)的取反操作, c k − 1 c_{k-1} ck−1的输入来自R端。J-K触发器具有良好的统计特性,但不能抵抗Ross Anderson的中间相遇一致性攻击和线性一致性攻击。
3.3 Pless生成器
为克服J-K触发器的缺点,Pless提是出了由多个J-K触发器序列驱动的多路复合序列方案,即Pless生成器。它由 8个LFSR、4个J-K触发器和1个循环计数器构成,由循环计数器进行选通控制。

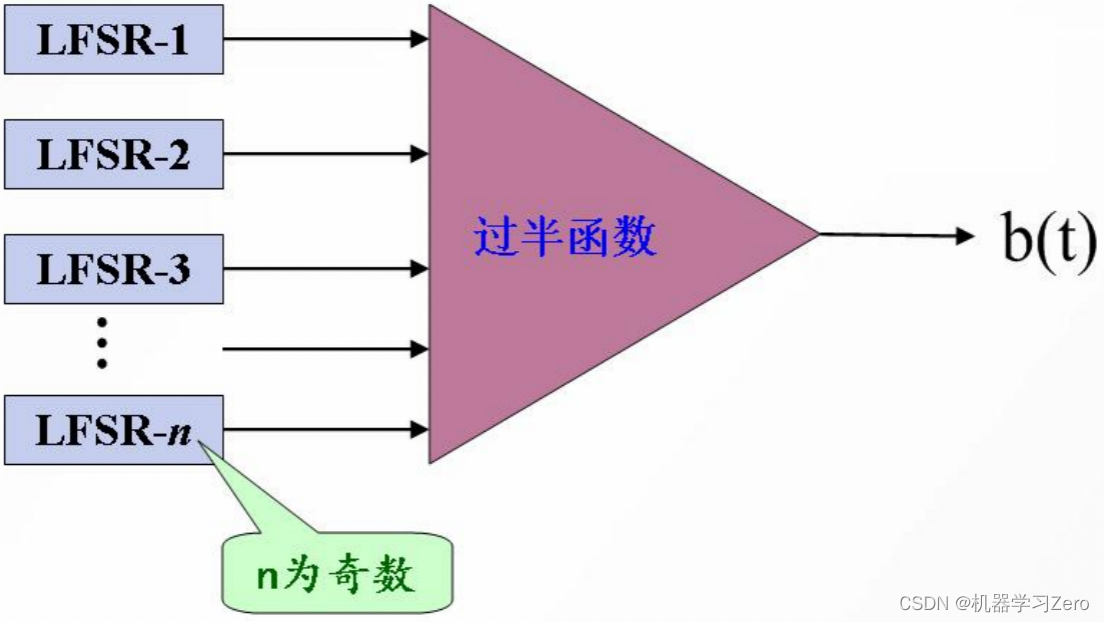
3.4 门限发生器
门限发生器通过使用可变数量的LSFR来避免相关安全性问题,但实质上难以抵看有关攻击,不建议使用。
4. 典型序列密码算法
4.1 RC4
RC4(Ron RivestCipher)以随机置换为基础,是一个可变密钥长度、面向字节操作的序列密码,该算法由于加解密速度快(比DES快约10倍)、易于软件实现,广泛应用于Microsoft Windows、Lotus Notes等软件中,以及安全套接字层(SSL,Secure Sockets Layer)传输信息。
与基于移位寄存器的序列密码不同,RC4是典型的基于非线性数组变换的序列密码。它以一个足够大的数组为基础,对其进行非线性变换,产生非线性的密钥序列,一般把这个大数组称为S盒。RC4的S盒的大小根据参数 n n n(通常 n = 8 n=8 n=8)的值变化,理论上来说,RC4算法可以生成总数为 N = 2 n N=2^n N=2n个的S盒。
**(1) 密钥调度算法(KSA,Key-Scheduling Algorithm)**用来设置S的初始排列。
首先,初始化S盒与向量T
S [ i ] = i , T [ i ] = K [ i m o d k e y L e n ] , i = 0 , 1 , . . . , 2 n − 1 S[i] = i, T[i] = K[i\mod keyLen],i = 0,1,...,2^n-1 S[i]=i,T[i]=K[imodkeyLen],i=0,1,...,2n−1其中, K K K为种子密钥, k e y L e n keyLen keyLen为种子密钥的长度(一般不低于128位)。
然后,利用向量T随机化S盒,对于 i = 0 , 1 , . . . , 2 n − 1 i = 0,1,...,2^n-1 i=0,1,...,2n−1,将 S [ i ] S[i] S[i]置换为 S [ j ] S[j] S[j],其中 j = ( j + S [ i ] + S [ j ] ) ( m o d 256 ) j= (j+S[i]+S[j])( \mod 256) j=(j+S[i]+S[j])(mod256)
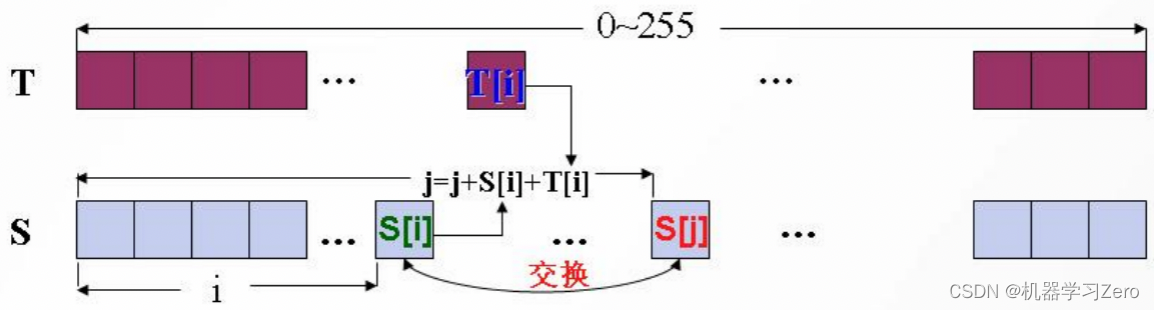
(2)伪随机生成算法(PRGA,Pseudo Random-Generation Algorithm) 用来选取随机元索并修改S的原始排列顺序,生成密钥流。首先,将 S [ i ] S[i] S[i]置换为 S [ j ] S[j] S[j],其中$ i= (i+1)(\mod 256), j= (j+S[i])( \mod 256)$,
然后,输出密钥 k = S [ t ] k = S[t] k=S[t],其中 t = ( S [ i ] + S [ j ] ) ( m o d 256 ) t = (S[i]+S[j])(\mod 256) t=(S[i]+S[j])(mod256)

加密时,将 k k k与明文字节异或;解密时,将 k k k与密文字节异或。举例
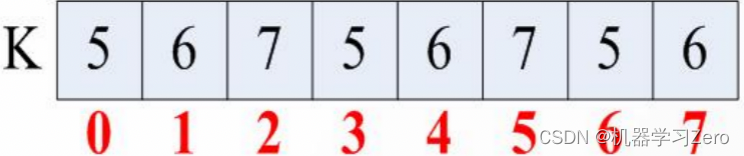
- 对于 n = 3 n=3 n=3的RC4,选取5、6、7作为密钥,初始化S盒与向量T:

- 利用向量T随机化S盒,如针对
i
=
0
,
j
=
0
i=0,j=0
i=0,j=0:
j
=
(
j
+
S
[
i
]
+
S
[
j
]
)
m
o
d
8
=
(
0
+
0
+
5
)
m
o
d
8
=
5
j=(j+S[i]+S[j])\mod 8= (0+0+5)\mod 8 = 5
j=(j+S[i]+S[j])mod8=(0+0+5)mod8=5则交换
S
[
0
]
S[0]
S[0]与
S
[
5
]
S[5]
S[5]。
循环执行结束后,S盒随机化如下:

- 使用S盒生成密钥流:
针对 i = 0 , j = 0 i=0,j=0 i=0,j=0: i = ( i + 1 ) m o d 8 = ( 0 + 1 ) m o d 8 = 1 i=(i+1)\mod 8 = (0+1)\mod 8 = 1 i=(i+1)mod8=(0+1)mod8=1 j = ( j + S [ i ] ) m o d 8 = ( 0 + S [ i ] ) m o d 8 = ( 0 + 4 ) m o d 8 = 4 j=(j+S[i])\mod 8= (0+S[i])\mod 8 =(0+4)\mod 8 = 4 j=(j+S[i])mod8=(0+S[i])mod8=(0+4)mod8=4交换 S [ 1 ] 、 S [ 4 ] S[1]、S[4] S[1]、S[4]

计算输出: t = ( S [ i ] + S [ j ] ) m o d 8 = ( S [ 4 ] + S [ 1 ] ) m o d 8 = ( 1 + 4 ) m o d 8 = 5 t = (S[i]+S[j])\mod 8=(S[4]+S[1])\mod 8 =(1+4)\mod 8 = 5 t=(S[i]+S[j])mod8=(S[4]+S[1])mod8=(1+4)mod8=5 k = S [ t ] = S [ 5 ] = 6 k=S[t]=S[5]=6 k=S[t]=S[5]=6 输出 k = 6 k=6 k=6(二进制 110 110 110)。
反复进行该过程,直到生产的而进度长度等于明文长度。
4.2 A5
A5算法是GSM 系统中要使用的序列密码加密算法之一,用于加密手机终端基站之间的传输的语音和数据,目前已被攻破。
该算法由一个22bit长的参数(帧号码, Fn)和64 bit长的参数(会话密钥,Kc)生成两个114 bit长的序列(密钥流),然后与GSM会话每帧(228 bit/帧)异或。
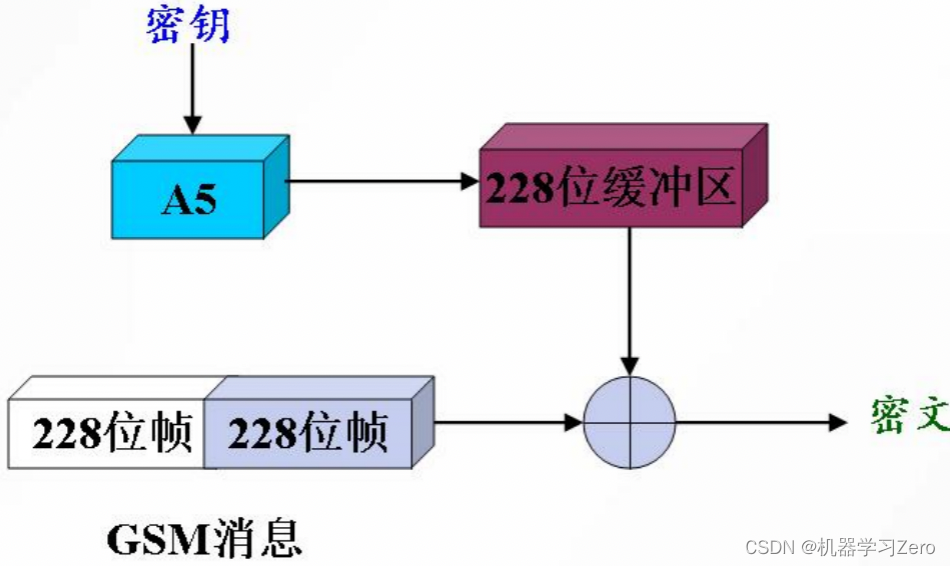
A5算法是一种典型的基于线性反馈移位寄存器的序列密码算法,构成A5加密器主体的LFSR有3个:A(19位)、B(22位)、C(23位),组成了一个集互控和停走于一体的钟控模型。这3个加密器的移位是由时钟控制的,且遵循“服从多数”的原则。即从每个寄存器中取出一个中间位进行运算判断,若在取出的3个中间位中至少有2个为“1”,则为“1”的寄存器进行一次移位,而为“0”的不移。反之,若3个中间位中至少有2个为“0”,则为“0”的寄存器进行一次移位,而为“1”的不移。

-
相关阅读:
【牛客网刷题】中秋节前开启java专项练习错题总结第一天
【重拾C语言】十二、C语言程序开发(穷举与试探——八皇后问题)
SQLServer统计监控SQL执行计划突变的方法
Linux上查询文件夹大小命令和删除命令
【原创】技术出身的我,如何做好一个管理者?
vmstat-内存性能分析常用命令
海贝造音强势登陆深圳 助力本土原创音乐升阶
leetcode-判断是不是二叉搜索树-92
包裹细胞膜的磁性纳米微载体/负载斑蝥素的巨噬细胞膜包封金属有机框架纳米颗粒的研究
单目3D目标检测[基于几何约束篇]
- 原文地址:https://blog.csdn.net/apr15/article/details/126943888