制作自己的软渲染器（二） 顶点缓冲与插值

在实时渲染过程中，我们最主要处理的对象就是顶点和片元。顶点是预设的，而片元的属性是我们通过顶点插值得出的。一个模型通常拥有一定规模的顶点，它们之间有一个最简单最重要的联系——哪些点是组成同一个三角形的。如果我们要进行多三角形的光栅化渲染，把这些数据组织好是很有必要的。

顶点缓冲数组

我最早是在 OpenGL 中了解这部分概念的。顶点的坐标我们可以装入数组中，然后规定数组的长度为 3 的倍数，并将每连续的 3 个顶点（也就是 9 个数值，每 3 个连续的数值为同一个顶点的坐标）设置为一组三角形。

这样做比较直观，但是有一个显然的问题：模型中的顶点通常是在多个三角形中重用的。例如一个立方体，每个面一个矩形需要通过两个三角形画出来，一共需要 12 个三角形，也就是 36 个顶点，但其实一个立方体只有 8 个顶点，于是我们存储了 24 个冗余的顶点数据。如果顶点数规模更大一点，我们可能浪费非常多的空间用于存储不必要的顶点数据。

减少数据冗余是非常有必要的。这个问题可以通过再创建一个顶点引用数组来解决。首先在顶点数组 a 中，每个顶点只存储一次。然后在顶点缓冲数组 b 中，每三个连续的整数表示某个三角形的三个顶点在 a 中的下标。例如我们现在有一个矩形，共四个顶点。在顶点数组中我们存储的是 {x0, y0, z0, x1, y1, z1, x2, y2, z2, x3, y3, z3}，而在顶点缓冲数组中我们存储的是 {0, 1, 2, 3, 1, 2}，表示 0,1,2 这三个顶点在同一个三角形上，而1,2,3 这三个顶点在另一个三角形上。

如果我们采用这样的数组组织方式，那么存一个立方体的数据大小就是 $3\times 8+12=36$，而使用原始的方法存储需要存 $3\times 36=108$ 个数。

三维空间中的顶点都是三维点，因为还没有摄像机，测试时先简单地将 $z$ 坐标掐掉（

尝试渲染一个矩形。数据如下：

double vertexBuffer[] = {
    200, 200, 0,
    200, 400, 0,
    400, 200, 0,
    400, 400, 0
};

int vertexIndex[] = {
    0, 1, 2,
    1, 2, 3
};

int tri_count = 6;

主函数中，用一个 for 循环读取数据并渲染。

for (int i = 0; i < tri_count * 3; i += 3) {
        drawTriangle(vertexBuffer[vertexIndex[i] * 3], vertexBuffer[vertexIndex[i] * 3 + 1],
            vertexBuffer[vertexIndex[i + 1] * 3], vertexBuffer[vertexIndex[i + 1] * 3 + 1],
            vertexBuffer[vertexIndex[i + 2] * 3], vertexBuffer[vertexIndex[i + 2] * 3 + 1],
            0xffffff
            );
    }

结果如下：

更多的顶点属性

如果要渲染出多种效果，每个顶点只有位置数据肯定时不够的。最简单地，我们希望顶点能拥有一个颜色属性，这样一个三角形就不会是单调的颜色了，至少我们不需要在渲染程序一个一个地为每个三角形指定颜色，而是在模型中就决定好。

改动我们的数据：

double vertexBuffer[] = {
    200, 200, 0, 0xff0000,
    200, 400, 0, 0x00ff00,
    400, 200, 0, 0x0000ff,
    400, 400, 0, 0x000000
};

int vertexIndex[] = {
    0, 1, 2,
    1, 2, 3
};

现在每个顶点有四个数据了，分别是三个轴的坐标和颜色值。

为了方便，drawTriangle 的参数列表也应该简化为顶点下标，否则顶点属性过多时参数列表会很长。

还有，为了更方便地指定各个属性，不妨把顶点也封装成结构体。

struct Vertex {
	double x, y, z;
	int color;

	kmath::vec3 operator - (const Vertex& another) {
		return kmath::vec3(this->x - another.x, this->y - another.y, this->z - another.z);
	}
};

于是数据变成这样了：

Vertex vertexBuffer[] = {
    {200, 200, 0, 0xff0000 },
    {200, 400, 0, 0x00ff00 },
    {400, 200, 0, 0x0000ff },
    {400, 400, 0, 0x000000 }
};

给顶点颜色值，但顶点只是一个矢量点，光栅化还是需要考虑片元。那么如何根据各个顶点的值确定片元的颜色呢？答案是插值（ interpolation）。一般会使用重心坐标插值法。

重心坐标插值

插值，即我们推算出的平均值。虽然这个位置没有给具体的值，但我通过其它给定的具体值，可以推算出这里的值设为多少是合理的。

如果我们设三角形 $ABC$ 中的一点 $P$ 的坐标完全用其与三个顶点的关系表示，就可以构造出一种方法为每个坐标插值。我们认定 $ABC$ 各点关于 $P$ 分别拥有一个权值 $\alpha ,\beta ,\gamma$，使得 $P=\alpha A+\beta B+\gamma C$，同时还有 $\alpha +\beta +\gamma =1$. 于是得到一个三元一次方程组，可以解出这三个值。最后的插值就是 $V_P=\alpha V_A+\beta V_B+\gamma V_C$.

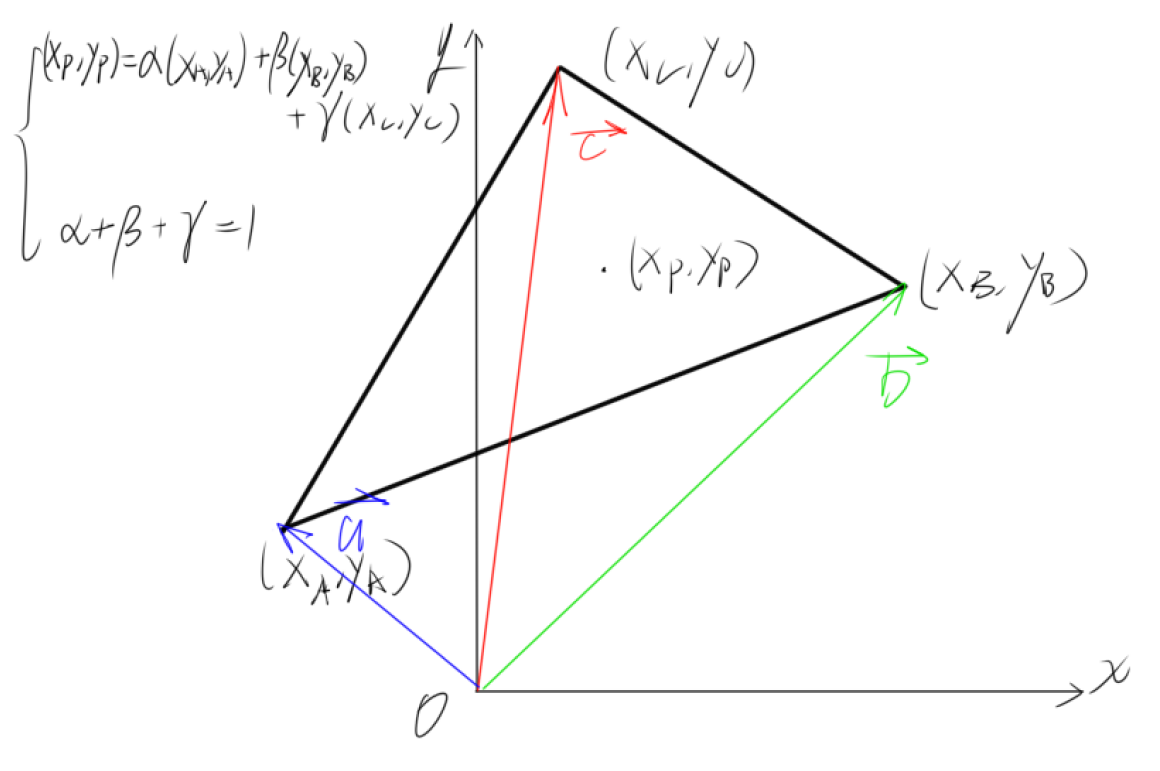
将这三个值解出来即可，我们认为 $P$ 的重心坐标是 $(\alpha ,\beta ,\gamma )$. 计算重心坐标的函数如下：

kmath::vec3f barycentric(kmath::vec2f p, kmath::vec2f a, kmath::vec2f b, kmath::vec2f c) {
    kmath::vec2f v0 = b - a, v1 = c - a, v2 = p - a;
    float d00 = v0 * v0;
    float d01 = v0 * v1;
    float d11 = v1 * v1;
    float d20 = v2 * v0;
    float d21 = v2 * v1;
    float denom = d00 * d11 - d01 * d01;
    float v = (d11 * d20 - d01 * d21) / denom;
    float w = (d00 * d21 - d01 * d20) / denom;
    return kmath::vec3f(1.0f - v - w, v, w);
}

（返回的 vec3f(u, v, w) 就是 p 的重心坐标）

现在，我的 drawTriangle 函数是这样。要注意 rgb 颜色值是存在一个 COLORREF 即 unsigned long 的六位十六进制中的，最高两位为 b 值，中间两位为 g 值，最下两位为 r 值。例如 0xff0000 表示纯蓝色。插值时这个数不能简单地加权而是要利用位运算把 rgb 分别考虑。

void drawTriangle(int xa, int ya, int xb, int yb, int xc, int yc, int c1, int c2, int c3) {
    kmath::vec2<int> v0(xb - xa, yb - ya);
    kmath::vec2<int> v1(xc - xa, yc - ya);
    kmath::vec2<int> v2;
    int xl = min(xa, min(xb, xc)), xr = max(xa, max(xb, xc));
    int yd = min(ya, min(yb, yc)), yu = max(ya, max(yb, yc));
    for (int i = xl; i <= xr; ++i) {
        for (int j = yd; j <= yu; ++j) {
            if (inTriangle(xa, ya, xb, yb, xc, yc, i, j)) {
                kmath::vec3f interpolate = barycentric(kmath::vec2f(i, j), kmath::vec2f(xa, ya), kmath::vec2f(xb, yb), kmath::vec2f(xc, yc));
                int b = interpolate.x * (c1 & 0x0000ff) + interpolate.y * (c2 & 0x0000ff) + interpolate.z * (c3 & 0x0000ff);
                b = b & 0x0000ff;
                int g = interpolate.x * (c1 & 0x00ff00) + interpolate.y * (c2 & 0x00ff00) + interpolate.z * (c3 & 0x00ff00);
                g = g & 0x00ff00;
                int r = interpolate.x * (c1 & 0xff0000) + interpolate.y * (c2 & 0xff0000) + interpolate.z * (c3 & 0xff0000);
                r = r & 0xff0000;
                putpixel(i, j, r | g | b);
            }
        } 
    }
}

这时，主函数中执行

for (int i = 0; i < tri_count * 3; i += 3) {
        drawTriangle(vertexBuffer[vertexIndex[i]].x, vertexBuffer[vertexIndex[i]].y,
        vertexBuffer[vertexIndex[i + 1]].x, vertexBuffer[vertexIndex[i + 1]].y,
        vertexBuffer[vertexIndex[i + 2]].x, vertexBuffer[vertexIndex[i + 2]].y,
        vertexBuffer[vertexIndex[i]].color, vertexBuffer[vertexIndex[i + 1]].color, vertexBuffer[vertexIndex[i + 2]].color);
    }

运行结果：

有人知道中间一条亮线是插值出的问题嘛。。总觉得怪怪的，不过应该没问题？

右下角的黑色换成白色就不会出现这样的亮线。

可能是因为两个三角形插值的颜色不同，上半三角形要亮于下半，所以边界处出现了上面比下面亮的情况？