-
数据结构(十二) -- 树(四) -- 霍夫曼树
1. 基本介绍
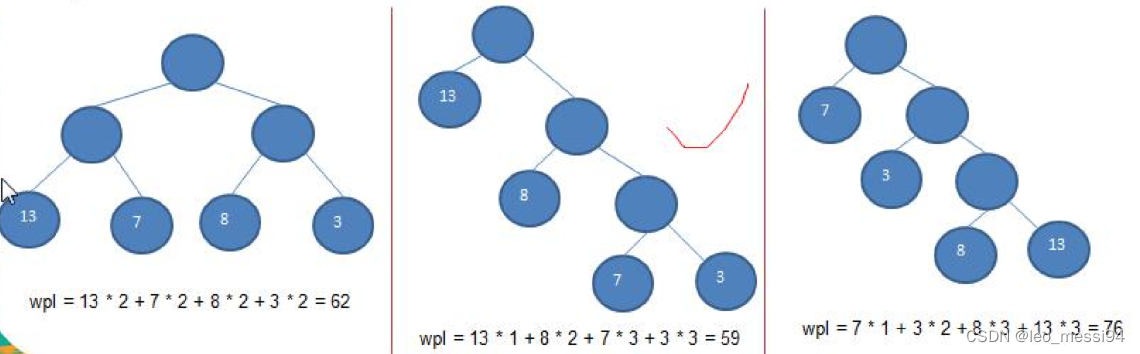
- 给定n个权值为n个叶子节点,构造一棵二叉树,若该树的带权路径长度(wpl)达到最小,称这样的二叉树为最优二叉树,也成为了霍夫曼树。
- 霍夫曼树是带权路径长度最短的树,权值较大的节点离根较近
2. 霍夫曼树的几个重要概念
- 路径和路径长度:在一棵树中,从一个节点往下可以达到的孩子或孙子节点之间的通路,成为路径。通路中分支的数目称为路径长度。若规定根节点的层数为1,则从根节点到第L层节点的路径长度为L-1
- 节点的权和带权路径长度:若将树中节点付给一个有着某种意义的数值,则这个数值成为该节点的权(值)。节点的带权路径长度为:从根节点到该节点之间的路径长度与该节点的权的乘积。
- 树的带权路径长度:树的带权路径长度规定为所有叶子节点的带权路径长度之和,记为WPL(weighted path length),权值越大的节点离根节点越近的二叉树才是最优二叉树
- WPI最小的就是霍夫曼树
3. 霍夫曼树创建
要求:给定一个数列{13,7,8,3,29,6,1},要求转成一个霍夫曼树。
3.1 构成霍夫曼树的步骤:
- 将每一个数据从小到大排序,每个数据都是一个节点,每个节点可以看成是一颗最简单的二叉树
- 取出根节点权值最小的两颗二叉树
- 组成一颗新的二叉树,该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
- 再将这颗新的二叉树,以根节点的权值大小,再次排序,不断重复上述步骤,直到数列中,所有的数据都被处理,就得到一颗霍夫曼树
- 图解:
- 数列:4,6,7,8,13,29

- 数列:7,8,10,13,29
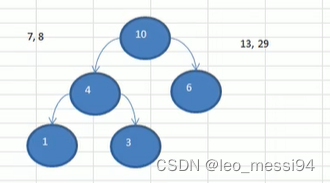
- 数列:10,13,15,29
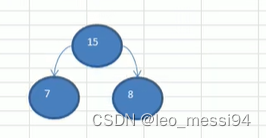
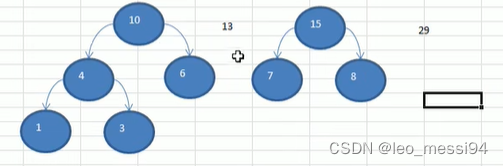
- 数列:15,23,29
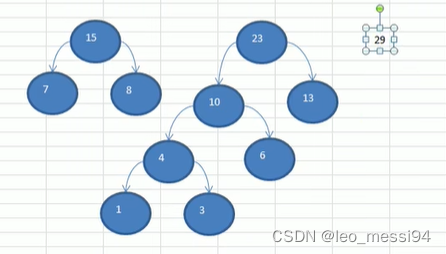
- 数列:29,38
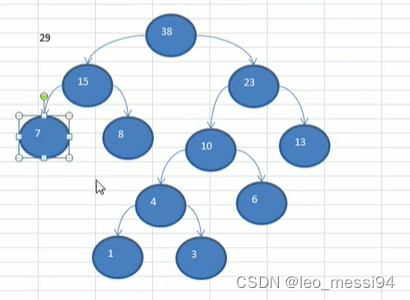
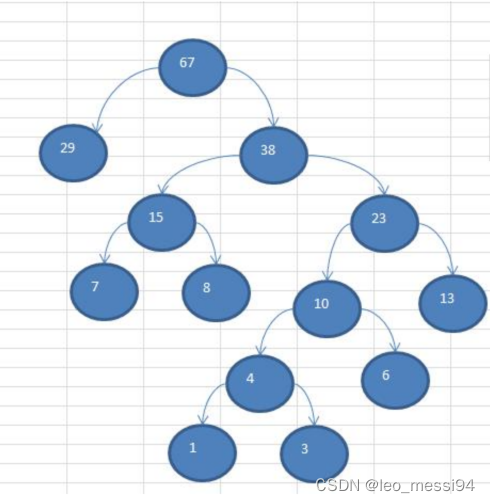
- 数列:4,6,7,8,13,29
3.2 代码实现:
public class HuffmanTree { public static void main(String[] args) { int arr[] = { 13, 7, 8, 3, 29, 6, 1 }; Node root = createHuffmanTree(arr); //测试一把 preOrder(root); // } //编写一个前序遍历的方法 public static void preOrder(Node root) { if(root != null) { root.preOrder(); }else{ System.out.println("是空树,不能遍历~~"); } } // 创建赫夫曼树的方法 /** * * @param arr 需要创建成哈夫曼树的数组 * @return 创建好后的赫夫曼树的root结点 */ public static Node createHuffmanTree(int[] arr) { // 第一步为了操作方便 // 1. 遍历 arr 数组 // 2. 将arr的每个元素构成成一个Node // 3. 将Node 放入到ArrayList中 List<Node> nodes = new ArrayList<Node>(); for (int value : arr) { nodes.add(new Node(value)); } //我们处理的过程是一个循环的过程 while(nodes.size() > 1) { //排序 从小到大 Collections.sort(nodes); System.out.println("nodes =" + nodes); //取出根节点权值最小的两颗二叉树 //(1) 取出权值最小的结点(二叉树) Node leftNode = nodes.get(0); //(2) 取出权值第二小的结点(二叉树) Node rightNode = nodes.get(1); //(3)构建一颗新的二叉树 Node parent = new Node(leftNode.value + rightNode.value); parent.left = leftNode; parent.right = rightNode; //(4)从ArrayList删除处理过的二叉树 nodes.remove(leftNode); nodes.remove(rightNode); //(5)将parent加入到nodes nodes.add(parent); } //返回哈夫曼树的root结点 return nodes.get(0); } } // 创建结点类 // 为了让Node 对象持续排序Collections集合排序 // 让Node 实现Comparable接口 class Node implements Comparable<Node> { int value; // 结点权值 char c; //字符 Node left; // 指向左子结点 Node right; // 指向右子结点 //写一个前序遍历 public void preOrder() { System.out.println(this); if(this.left != null) { this.left.preOrder(); } if(this.right != null) { this.right.preOrder(); } } public Node(int value) { this.value = value; } @Override public String toString() { return "Node [value=" + value + "]"; } @Override public int compareTo(Node o) { // TODO Auto-generated method stub // 表示从小到大排序 return this.value - o.value; } }4. 霍夫曼编码
4.1 基本介绍

4.2 原理剖析
通信领域中信息的处理方式:
-
定长编码:
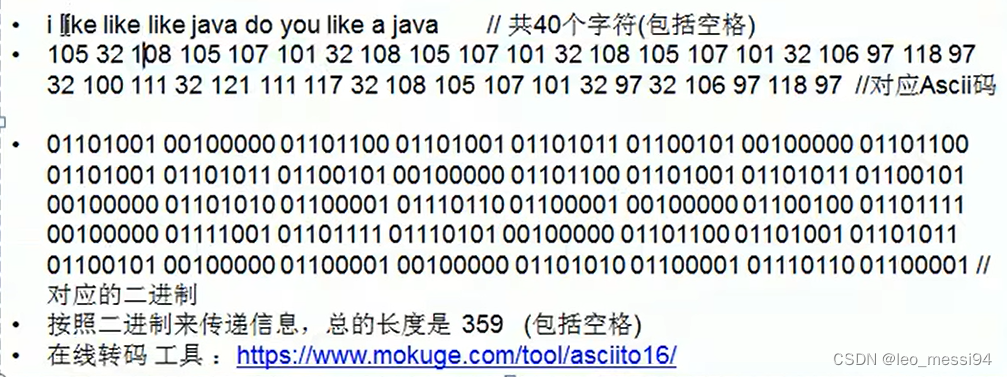
-
变长编码:目前存在匹配的多意性,比如10010110100,我们是理解成10 0 101 10 100,但是机器也能理解成1 0 0 。。。。

-
霍夫曼编码

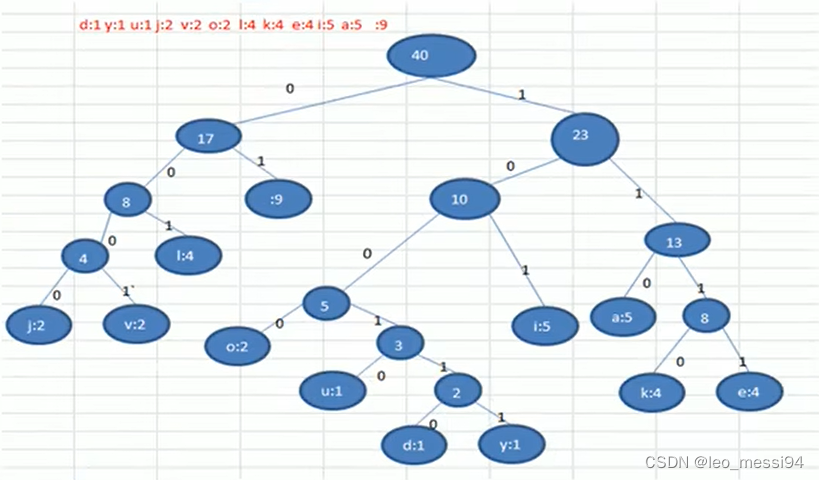

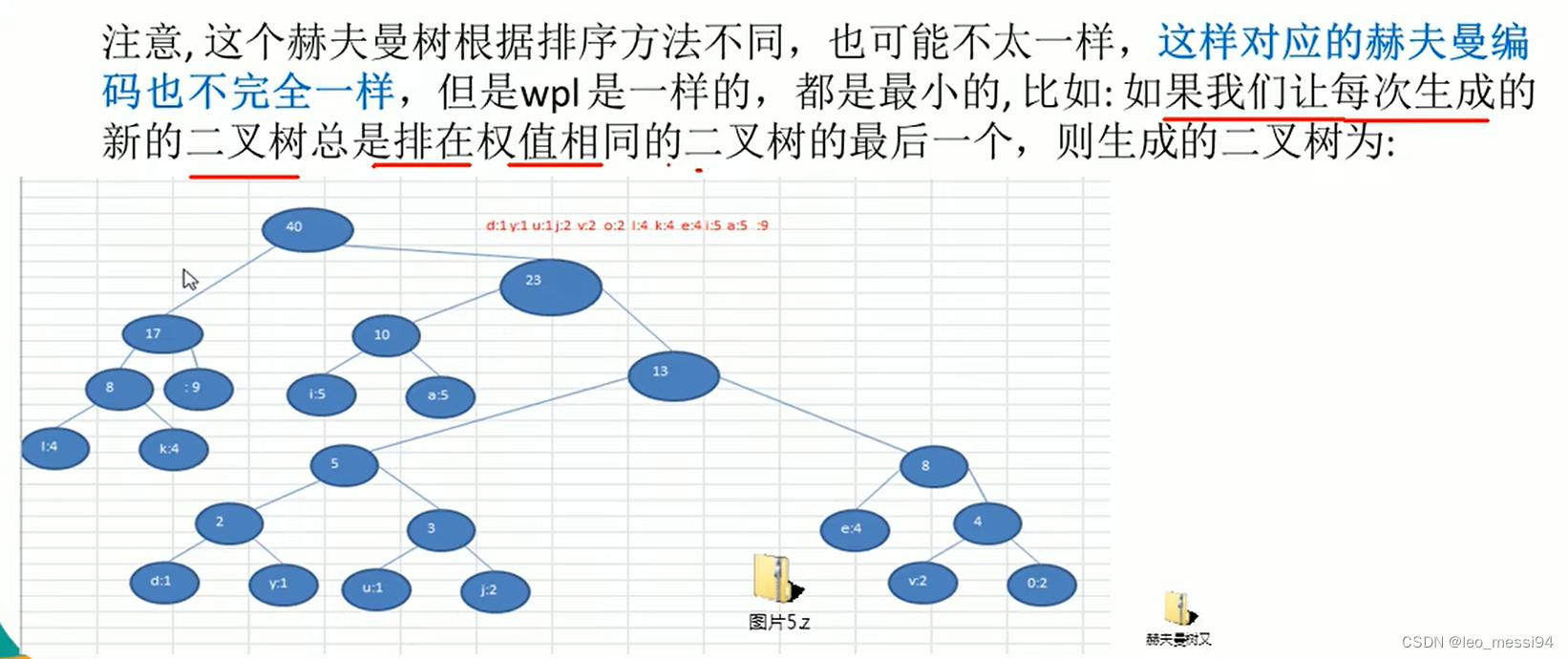
注意:在获取字符出现次数时,可能出现重复的情况,但是这个不影响,我们生成的霍夫曼的树不一样,但是树的权(WPL)还是一样的,也就是压缩效率还是一致的。
4.3 使用霍夫曼树进行数据压缩
4.3.1 要求:

4.3.2 思路:

4.3.3 代码编写:
- Node类,代表霍夫曼树的一个节点:
//创建Node ,待数据和权值 class Node implements Comparable<Node> { Byte data; // 存放数据(字符)本身,比如'a' => 97 ' ' => 32 int weight; //权值, 表示字符出现的次数 Node left;// Node right; public Node(Byte data, int weight) { this.data = data; this.weight = weight; } @Override public int compareTo(Node o) { // 从小到大排序 return this.weight - o.weight; } public String toString() { return "Node [data = " + data + " weight=" + weight + "]"; } //前序遍历 public void preOrder() { System.out.println(this); if(this.left != null) { this.left.preOrder(); } if(this.right != null) { this.right.preOrder(); } } }- 接收字节数组并转成node
/** * 步骤一: * @param bytes 接收字节数组 * @return 返回的就是 List 形式 [Node[date=97 ,weight = 5], Node[]date=32,weight = 9]......], */ private static List<Node> getNodes(byte[] bytes) { //1创建一个ArrayList ArrayList<Node> nodes = new ArrayList<Node>(); //遍历 bytes , 统计 每一个byte出现的次数->map[key,value] Map<Byte, Integer> counts = new HashMap<>(); for (byte b : bytes) { Integer count = counts.get(b); if (count == null) { // Map还没有这个字符数据,第一次 counts.put(b, 1); } else { counts.put(b, count + 1); } } //把每一个键值对转成一个Node 对象,并加入到nodes集合 //遍历map for(Map.Entry<Byte, Integer> entry: counts.entrySet()) { nodes.add(new Node(entry.getKey(), entry.getValue())); } return nodes; }- 将node列表转成霍夫曼树:
// 步骤二: //将getNodes方法生成的Node列表转变成对应的赫夫曼树,并返回最后的根节点 private static Node createHuffmanTree(List<Node> nodes) { while(nodes.size() > 1) { //排序, 从小到大 Collections.sort(nodes); //取出第一颗最小的二叉树 Node leftNode = nodes.get(0); //取出第二颗最小的二叉树 Node rightNode = nodes.get(1); //创建一颗新的二叉树,它的根节点 没有data, 只有权值 Node parent = new Node(null, leftNode.weight + rightNode.weight); parent.left = leftNode; parent.right = rightNode; //将已经处理的两颗二叉树从nodes删除 nodes.remove(leftNode); nodes.remove(rightNode); //将新的二叉树,加入到nodes nodes.add(parent); } //nodes 最后的结点,就是赫夫曼树的根结点 return nodes.get(0) -
相关阅读:
Rust中的过程宏
高速串行总线——SATA
50.Python-web框架-Django中引入静态的bootstrap样式
家里蹲了七个月的大学生活是怎么度过的?
GeForce RTX 2080显卡驱动安装(linux系统)
理解Python装饰器
torch.nn.Linear(in_features, out_features, bias=True)[source]
vue如何自定义路由菜单
Onnxruntime之图像分类(c++)
rocky8安装docker步骤
- 原文地址:https://blog.csdn.net/weixin_39724194/article/details/126938294