【JAVA数据结构】Stack栈的深度剖析

春来夏往，秋收冬藏，我们来日方长

大家好，这里是新一，请多关照🙈🙉🙊。在本篇博客中，新一将会为大家介绍JAVA数据结构 - Stack，干货满满哟。（以下结果均在IDEA中编译）希望在方便自己复习的同时也能帮助到大家。😜😜😜🥇🥈🥉

废话不多说，直接进入我们的文章。

---

---

一 .🌕 栈的概念及方法实现

1.1🍂 概念

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据在栈顶

对于栈，最重要的一点当然是 先进后出，后进先出

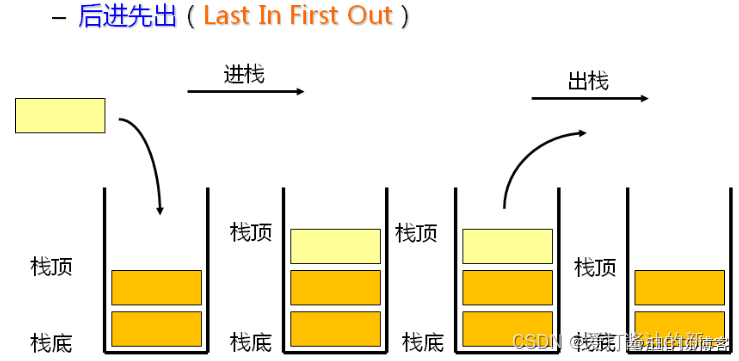
以下是压栈，弹出过程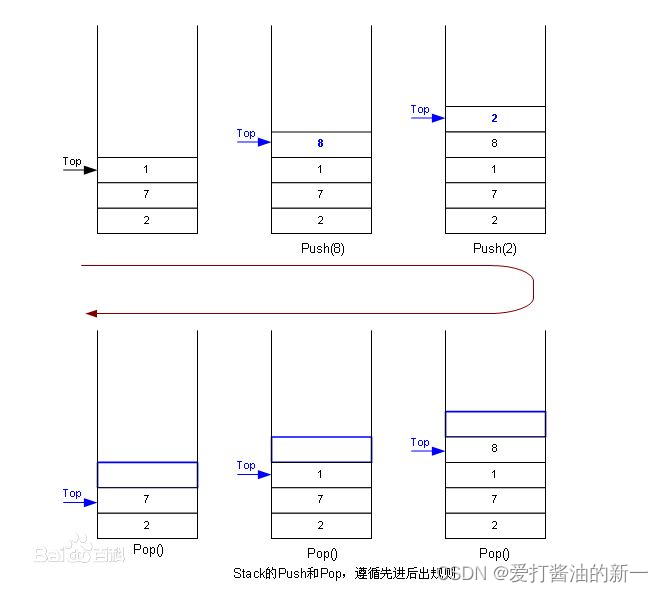

1.2🍂 方法实现

1.2.1 🍃 push(压栈）&& pop(弹出）

public static void main(String[] args) {
        MyStack stack = new MyStack();
        stack.push(1);
        stack.push(2);
        stack.push(3);
        stack.push(4);
        stack.push(5);
        stack.push(6);
        //弹出栈顶元素，并删除
        System.out.println(stack.pop());//6
    }
1
2
3
4
5
6
7
8
9
10
11

1.2.2 🍃 peek(获取栈顶元素) && isEmpty(判空)

public static void main(String[] args) {
        MyStack stack = new MyStack();
        stack.push(5);
        stack.push(6);
        System.out.println(stack.pop());//弹出栈顶元素，并删除 - 6
        System.out.println(stack.peek());//获取栈顶元素，不删除 - 5
        System.out.println(stack.peek());//获取栈顶元素，不删除 - 5
        System.out.println(stack.isEmpty());//false
    }
1
2
3
4
5
6
7
8
9

1.3🍂 模拟实现MyStack

这里我们底层利用顺序表实现我们的Stack，采用尾插加尾删即可

public class MyStack {
    public int[] elem;
    public int usedSize;

    public MyStack() {
        this.elem = new int[5];
    }

    public void push(int val){
        if (isFull()){
            //扩容
            this.elem = Arrays.copyOf(this.elem,this.elem.length * 2);
        }
        this.elem[usedSize] = val;
        this.usedSize++;
    }

    public boolean isFull() {
        return this.usedSize == this.elem.length;
    }

    public int pop(){
        if (isEmpty()){
            throw new RuntimeException("栈为空！");
        }
        //this.elem[this.usedSize - 1] = null;//引用类型需要置空
        int oldVal = this.elem[usedSize - 1];
        usedSize--;
        return oldVal;
    }

    public boolean isEmpty(){
        return this.usedSize == 0;
    }

    public int peek(){
        if (isEmpty()){
            throw new RuntimeException("栈为空！");
        }
        return this.elem[usedSize - 1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

那么我们能否用链表实现呢，可以是可以，那在加个条件，能不能在O(1)时间复杂度下完成，显然单链表是做不到的，如果想要做到，那就必须使用带有尾结点的双向链表，可以看看我这篇博客 双向链表的增删查改

二 .🌕 栈典型例题

第一题：逆波兰式求值

👇👇👇
做题链接戳这里：150.逆波兰式求值

🍂 题目描述

根据 逆波兰表示法，求表达式的值。

有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

注意 两个整数之间的除法只保留整数部分。

可以保证给定的逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

🍂示例

输入：tokens = [“2”,“1”,“+”,“3”,“*”]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例2

输入：tokens = [“4”,“13”,“5”,“/”,“+”]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例3

输入：tokens = [“10”,“6”,“9”,“3”,“+”,“-11”,““,”/“,””,“17”,“+”,“5”,“+”]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

🍂提示

● 1 <= tokens.length <= 104
● tokens[i] 是一个算符（“+”、“-”、“*” 或 “/”），或是在范围 [-200, 200] 内的一个整数

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。
平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点：

● 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
● 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中

此外，我们如果遇到客观题要求我们将一个中缀表达式写成后缀表达式呢？

其实很简单，这里新一教大家一个方法，比如这个 （5 + 3）* 2 - 6，我们只需将运算部分每一部分加括号，然后把数字写在前面，遇到括号，再写括号对应的运算符，即（5 3 + 2 * 6 - ）💕

🍃题解

这是一道很常见的例题，我们要求后缀表达式的值，那么我们遇到数字必须压栈，然后遇到操作符就弹出两个操作数进行运算，在将结果再度压栈，知道遍历完我们的字符串最后栈顶的那个数即为我们要求的值，这里我将判断操作数写成了一个方法便于运算

class Solution {
    public int evalRPN(String[] tokens){
        Stack<Integer> stack = new Stack<>();
        for (int i = 0; i < tokens.length; i++) {
            String val = tokens[i];
            if (isOperation(val) == false){
                stack.push(Integer.parseInt(val));
            }else{
                int num2 = stack.pop();
                int num1 = stack.pop();
                switch(val){
                    case "+":
                        stack.push(num1 + num2);
                        break;
                    case  "-":
                        stack.push(num1 - num2);
                        break;
                    case "*":
                        stack.push(num1 * num2);
                        break;
                    case "/":
                        stack.push(num1 / num2);
                        break;
                }
            }
        }
        return stack.pop();
    }
    private boolean isOperation(String x){
        if (x.equals("+") || x.equals("-")|| x.equals("*")|| x.equals("/")){
            return true;
        }
        return false;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

第二题：栈的压入、弹出序列

👇👇👇
做题链接戳这里：JZ31.栈的压入、弹出序列

🍂 题目描述

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。

🍂示例

输入：
[1,2,3,4,5],[4,5,3,2,1]
返回值：true
说明：可以通过push(1)=>push(2)=>push(3)=>push(4)=>pop()=>push(5)=>pop()=>pop()=>pop()=>pop()这样的顺序得到[4,5,3,2,1]这个序列，返回true

示例2

输入：
[1,2,3,4,5],[4,3,5,1,2]
返回值：false
说明：由于是[1,2,3,4,5]的压入顺序，[4,3,5,1,2]的弹出顺序，要求4，3，5必须在1，2前压入，且1，2不能弹出，但是这样压入的顺序，1又不能在2之前弹出，所以无法形成的，返回false
示例3

🍂提示

● 1. 0<=pushV.length == popV.length <=1000
● 2. -1000<=pushV[i]<=1000
● 3. pushV 的所有数字均不相同

🍃题解

要判断栈的弹出序列是否匹配，我们就必须先将目标序列压栈，然后再逐个遍历待判序列，如果相等，弹出栈顶元素，继续判断，直到不相等，然后继续压栈，最终遍历完我们整个目标序列即全部压栈完成，如果为栈为空，那么说明我们的待判序列成功将我们的栈内元素全部弹出，换句话说，也就是完全匹配才会为空

import java.util.Stack;

public class Solution {
    public boolean IsPopOrder(int [] pushA, int [] popA) {
        Stack<Integer> stack = new Stack<>();
        int i = 0;
        int j = 0;
        while (i < pushA.length && j < popA.length){
            stack.push(pushA[i]);
            while (j < popA.length && !stack.empty() && stack.peek() == popA[j]){
                stack.pop();
                j++;
            }
            i++;
        }
        return stack.empty();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

想对大家说的话

家人们，学到这里我们的JAVA的Stack栈的深度剖析到这里就结束啦啦，🥳🥳🥳，后续新一会持续更JAVA的有关内容，学习永无止境，技术宅，拯救世界！