Cplex是一种数学优化技术。主要用于提高效率、快速实现策略并提高收益率。Cplex提供灵活的高性能优化程序，解决线性规划 (Linear Programming)、二次方程规划 (Quadratic Programming)、二次方程约束规划 (Quadratically Constrained Programming) 和混合整型规划 (Mixed Integer Programming) 问题。

在Eclipse下配置Cplex环境参考：在Ecplise下调用Cplex环境配置

一. 前言

目前基于Java的Cplex求解规划问题的文章或是教程并不算多，新手入门只能通过官方文档和别人少量的程序中总结摸索。我最近也在做规划相关的项目，在这里将我一些学习的心得和编码技巧分享给大家。

官网的界面如下图所示，大家根据自己Cplex的版本在左边选择对应版本的教程。入门时大家可以先从Getting Started with CPLEX开始，然后可以自己随便翻一翻看一看，但是我认为最重要的部分就是下面这个CPLEX Java Reference Manual，里面包含了所有API的使用方法及说明：

其中ilog.concert库包含了跟变量的定义相关的，例如优化变量的定义，表达式的定义等；ilog.cplex库包含了跟模型相关的，比如各类模型的定义，算法等。文档里给的API有非常多，但是常用的其实就那几个，接下来我将介绍一下Cplex编程的一般流程及常用接口。

二. Cplex入门

2.1 程序模板

Cplex程序的模板通常如下所示，我们只需要在相应的位置填写内容即可：

import ilog.concert.*;
import ilog.cplex.*;

public class Cplex{ //类的名字必须跟.java的名字一样
 
	public static void main(String[] args) {
		try {
			// 1. 创建模型
			
			// 2. 定义优化参数
			
			// 3. 设置目标函数

			// 4. 设置约束
			
			// 5. 模型求解及输出
						
		} catch (IloException e) {
			System.err.println("Concert exception caught: " + e);
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

2.2 创建模型

IloCplex cplex = new IloCplex(); // creat a model
1

2.3 定义优化参数

这里定义将要求解的优化参数，参数类型包括单个变量、一维及二维数组类型。

//1.单个变量
//1.1 实数型变量
IloNumVar x= cplex.numVar(0, 5); 
//1.2 整型变量
IloIntVar x= cplex.intVar(0, 5); 
/*括号中的参数表示变量的取值范围，例如该变量的取值范围为0≤x≤5，若不想定义范围可以设置为-Double.MAX_VALUE和Double.MAX_VALUE，表示负无穷到正无穷*/

//2. 一维数组
// 2.1 实数型变量
IloNumVar[] x = cplex.numVarArray(3, 0.0, 5.0);
// 2.2 整型变量
IloIntVar[] x = cplex.intVarArray(3, 0, 5);
/*括号中的参数表示数组的大小、最小值和最大值*/
// 2.3 每个变量设置不同的范围
double[] rg = {0,5,1,2,4,5}; //每个变量的最小值和最大值
IloNumVar[] a = new IloNumVar[3];
for(int i=0;i<3;i++)
{
	a[i] = cplex.numVar(rg[2*i], rg[2*i+1]);
}
/*这种方式就将数组中的三个变量设置了不同的取值范围，分别为0-5，1-2，4-5*/

//3. 二维数组
//3.1 实数型变量
IloNumVar[][] x = new IloNumVar[2][];
for (int i=0; i<2; i++) 
{
	x[i] = cplex.numVarArray(2, 0.0, 5.0);
}
//3.2 整型变量
IloIntVar[][] x = new IloIntVar[2][];
for (int i=0; i<2; i++) 
{
	x[i] = cplex.intVarArray(2, 0, 5);
}
/*以上这种方式定义了2行2列的变量，变量范围为0-5，若像设置不同的取值范围，按照一维数组的方式修改即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

2.4 设置目标函数及约束

目标函数一般是取一个表达式的最大值或是最小值，约束一般是设定一个表达式的取值范围，他们有一个共同点就是都需要先定义表达式，而且他们定义表达式的方式是完全相同的。

2.4.1 定义表达式

如图所示，最后四个字母为Expr的方法即为可以定义的表达式类型：

官方根据表达式类型的不同提供了不同的接口，包括：

大家可以根据自己表达式类型的不同选择适合自己接口形式，例如我的表达式为x1+2*x2+3*x3，属于线性类型，那么就可以一次线性表达式的接口：

//定义变量
IloNumVar[] x = cplex.numVarArray(3, -5, 5);

IloLinearNumExpr cs= cplex.linearNumExpr();
cs.addTerm(1, x[0]);
cs.addTerm(2, x[1]); 
cs.addTerm(3, x[2]);
1
2
3
4
5
6
7

每个接口都提供了非常多的方法，大家可以在官方文档中查看各个接口的使用方法及说明。

尽管官方为不同形式的表达式提供了不同的接口，但是存在一定的问题，比如你无法在一次线性表达式中添加二次项，当表达式比较复杂的时候通常不止有一种类型。因此我比较习惯于就用最基本的公式接口IloNumExpr，在这个接口中你可以利用cplex模型库中的加减乘除来添加任何形式表达式。

先创建模型IloCplex cplex = new IloCplex();后就可以通过cplex.XXX的方式使用模型中各种运算方法，常用的包括：

有了以上这四种方法基本就可以应对大部分的表达式了，例如上面那个表达式x1+2*x2+3*x3，用基本公共接口表示为：

IloNumVar[] x = cplex.numVarArray(3, -5.0, 5.0);
					
double[] a = {1,2,3};
IloNumExpr cs = cplex.numExpr();
for(int i=0;i<3;i++)
{
	cs = cplex.sum(cs,cplex.prod(x[i], a[i]));
}
1
2
3
4
5
6
7
8

虽然这种方式增加了代码量，但是代码的可读性增强了，所以我更喜欢用这种方式定义表达式。

下面我再举一个例子，求变量x的平方和和绝对值之和：

IloNumVar[] x = cplex.numVarArray(3, -5.0, 5.0);

IloNumExpr cs1 = cplex.numExpr();
IloNumExpr cs2 = cplex.numExpr();
for(int i=0;i<3;i++)	
{
	cs1= cplex.sum(cs1,cplex.abs(x[i])); //绝对值之和
	cs2= cplex.sum(cs2,cplex.prod(x[i], x[i])); //平方和
}	
1
2
3
4
5
6
7
8
9

在定义了表达式之后就可以添加目标函数和约束了。

2.4.2 定义目标函数

假设定义后目标函数的表达式用obj表示：

2.4.3 定义约束

假设定义后约束的表达式用cs表示：

在添加了约束后我们可以通过cplex.diff(cs,cs)来清空表达式cs，然后就可以在cs中添加新的表达式。

2.5 模型求解及输出

模型求解及输出的模板如下所示：

if (cplex.solve()) {
cplex.output().println("Solution status = " + cplex.getStatus());
cplex.output().println("Solution value = " + cplex.getObjValue());
double[] val = cplex.getValues(x);
for (int j = 0; j < val.length; j++)
	System.out.println("x" + (j+1) + "  = " + val[j]);
}
cplex.end();
1
2
3
4
5
6
7
8

其中：

模型求解包括以下几个状态：

三. 案例展示

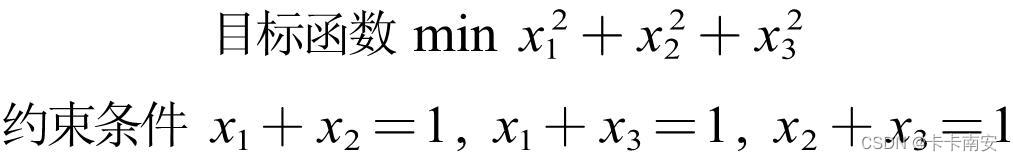
import ilog.concert.*;
import ilog.cplex.*;

public class test {
	public static void main(String[] args) {
		try {
			IloCplex cplex = new IloCplex(); // create a model
			
			IloNumVar[] x = cplex.numVarArray(3, -Double.MAX_VALUE, Double.MAX_VALUE);
			
			IloNumExpr cs1 = cplex.numExpr();
			for(int i=0;i<3;i++)
			{
				cs1 = cplex.sum(cs1,cplex.prod(x[i], x[i]));
			}
				
			cplex.addMinimize(cs1);
			
			cplex.addEq(cplex.sum(x[0], x[1]),1);
			cplex.addEq(cplex.sum(x[0], x[2]),1);
			cplex.addEq(cplex.sum(x[1], x[2]),1);
					
			if (cplex.solve()) {
				cplex.output().println("Solution status = " + cplex.getStatus());
				cplex.output().println("Solution value = " + cplex.getObjValue());
				double[] val = cplex.getValues(x);
				for (int j = 0; j < val.length; j++)
					System.out.println("x" + (j+1) + "  = " + val[j]);
			}
			cplex.end();
			
		} catch (IloException e) {
			System.err.println("Concert exception caught: " + e);
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

运行结果为：

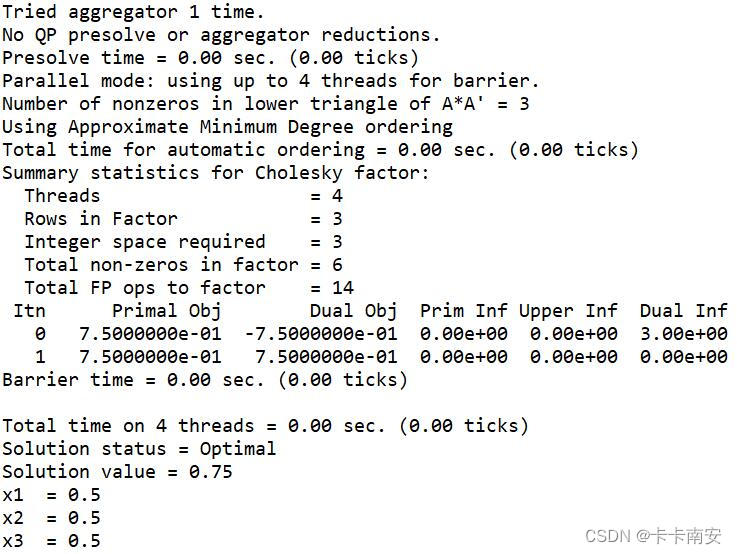
程序比较简单这里不再做讲述，大家可以结合第二部分的内容理解一下。

总而言之，别人的程序、官方文档和官方案例是学习Cplex的最好教程，希望大家多加摸索！