并查集及实现

并查集

并查集是一种树形的数据结构，主要用于解决一些元素分组的问题。用于处理一些不相交集合的合并以及查询问题。
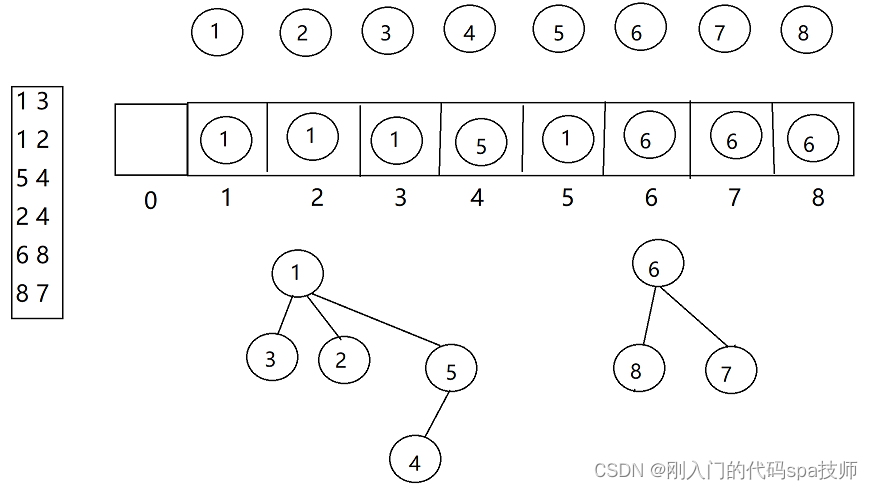
并查集的思想是用一个数组表示了整片森林，树的根节点唯一标识了一个集合，我们只要找到了某个元素的树根，就能确定它在哪个集合里。

如下图，有八个节点，节点13，12，54，24，68，87间存在关联，以左边的节点为父节点，可以得到六个有两个节点的树形结构。并查集的相关接口主要是若干元素合并到一个或者多个集合（构成一棵树或多棵树）、查询两个元素是否在同一个集合中（节点是否在同一颗树中）、存在几个集合（有几棵树）

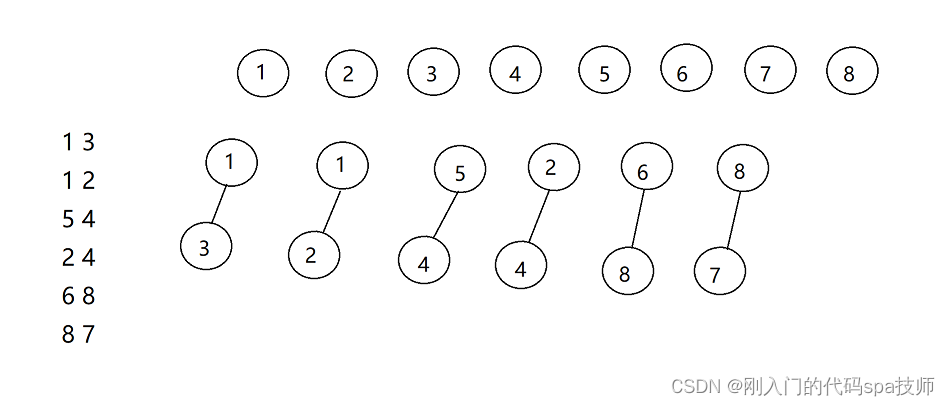
合并

并查集构建过程：把节点所在的树的根节点进行合并即可。
将若干元素合并到一个或者多个集合（构成一棵树或多棵树），将多个集合合并（多颗树合并为一棵树）。
合并13和12：因为3和2都有共同的父节点1，把2和3都挂在1下即可。

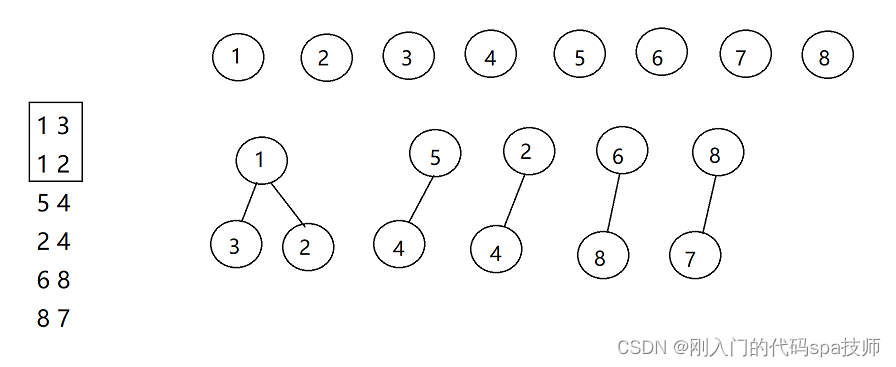
合并132，54，24：对于132和54、24这三棵树，4有5和2两个节点有关系，合并这三棵树只需要把节点所在的树的根节点进行合并即可。

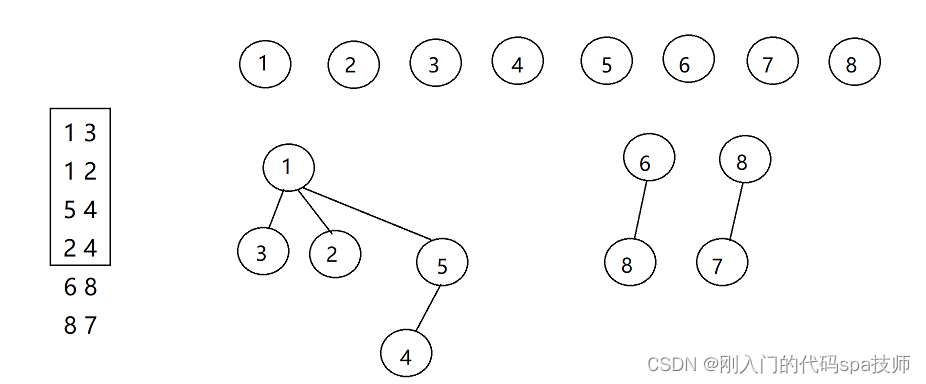
最终合并所得并查集：

查询

查询两个元素是否在同一个集合中，只需判断两个节点所在的树的根是否相同。如果相同，则在一个集合中，否则不在一个集合。

并查集的表示

并查集是一种树形的数据结构，对于这棵树长什么样，我们并不关心，只需要能表示两个点是否在一个集合中就可以了。
并查集的主要操作就是合并和查询，这需要依赖一个数组来实现他们。要表示节点间的关系，只需把每一个节点对应的数组元素的位置，存储它父节点的编号即可。
表示及初始化如下图，初始化每个节点表示一个独立的集合。

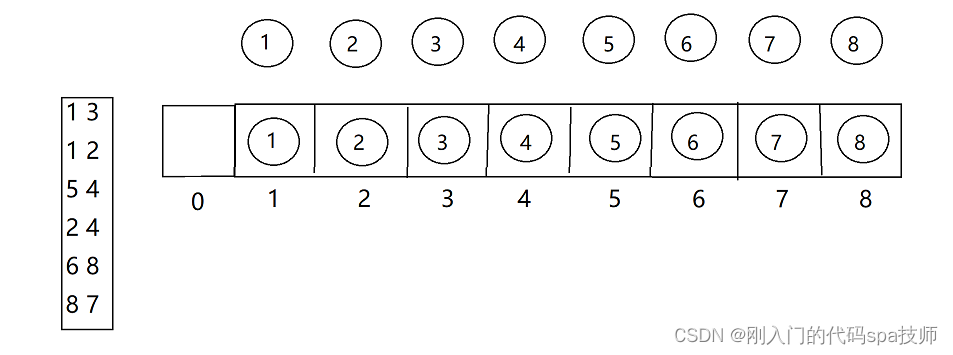
构建完成的并查集：

判断当前节点是否是根节点，只需判断节点存储的编号是否和数组下标相等即可。

#include 
#include 
using namespace std;

struct MFSet_struct {
	int key;
	int val;
	MFSet_struct(int k, int v) :key(k), val(v) {}
};
class MergeFindSet
{
public:
	MergeFindSet(vector<MFSet_struct>& vec) :parent(vec) {};

	//非递归查询
	int find(int x)
	{
		while (x != parent[x].key)
		{
			x = parent[x].key;
		}
		return x;
	}
	//递归查询
	int rfind(int x)
	{
		if (x == parent[x].key)
		{
			return x;
		}
		else
		{
			return rfind(parent[x].key);
		}
	}
	//合并
	void merge(int x, int y)
	{
		int a = find(x);
		int b = find(y);
		if (a == b) return;
		parent[y].key = a;
	}

private:
	vector<MFSet_struct> parent;
};

int main()
{
	//构建初始化数组
	vector<MFSet_struct> parent;
	for (int i = 0; i < 9; i++)
	{
		parent.emplace_back(i, i);
	}

	//构建并查集
	MergeFindSet mf(parent);
	int x, y;
	for (int i = 0; i < 6; i++)
	{
		cin >> x >> y;
		mf.merge(x, y);
	}

	cout << (mf.find(2) == mf.find(8) ? "OK" : "NO") << endl;
	cout << (mf.find(2) == mf.find(4) ? "OK" : "NO") << endl;
	cout << (mf.find(3) == mf.find(6) ? "OK" : "NO") << endl;
	cout << (mf.find(1) == mf.find(6) ? "OK" : "NO") << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

查询优化：路径压缩

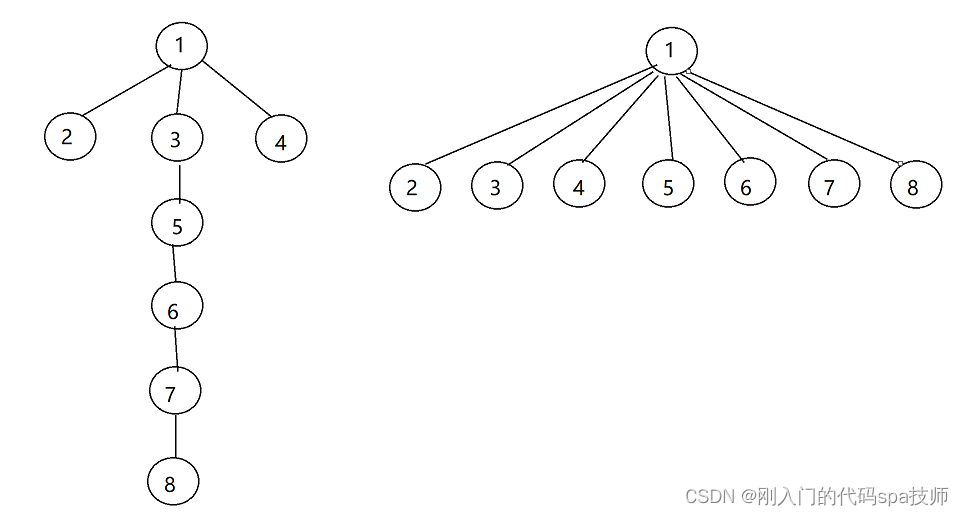
大多数情况下，在查询过程中只关心根节点是什么，并不关系这棵树的形态，我们希望树的结构越矮越好。因此在查询操作的时候将访问过的每个点的父节点修改成树根，这样的方法叫做路径压缩。

在构造并查集的过程中，可能会出现并查集的某一条到叶子节点路径过深的问题，我们希望得到的是右边这样矮胖的树，而不是左边这样瘦高的树。

为了优化并查集的结构，有两种路径压缩的方法：优化find和加权标记。

优化find：在find过程中优化
在并查集的find过程中，可以在查询的过程中把查询路径上节点的父节点编号修改为根节点，使用递归查询可以把查询路径上的所有结点的父节点编号都置为根节点编号，而非递归查询只能修改一个。

	//递归查询
	int rfind(int x)
	{
		if (x == parent[x].key)
		{
			return x;
		}
		else
		{
			parent[x].key = rfind(parent[x].key);
			return parent[x].key;
		}
	}
1
2
3
4
5
6
7
8
9
10
11
12
13

加权标记：在merger过程中优化
在上面merger合并的过程中，永远都是一个方向上的合并，并未考虑树的高低。
我们的期望是在并查集构建的过程中，进行集合合并的时候，尽量使合并后的集合树的高度矮一些，尽量使高度矮的树挂到高度高的树根节点下。

#include 
#include 
using namespace std;

struct MFSet_struct {
	int key;
	int val;
	MFSet_struct(int k, int v) :key(k), val(v) {}
};
class MergeFindSet
{
public:
	MergeFindSet(vector<MFSet_struct>& vec) :parent(vec),rank(vec.size(), 1) {};

	//非递归查询
	int find(int x)
	{
		while (x != parent[x].key)
		{
			x = parent[x].key;
		}
		return x;
	}
	//递归查询
	int rfind(int x)
	{
		if (x == parent[x].key)
		{
			return x;
		}
		else
		{
			//parent[x].key = rfind(parent[x].key);
			//return parent[x].key;
			return rfind(parent[x].key);
		}
	}
	//合并
	void merge(int x, int y)
	{
		int a = find(x);
		int b = find(y);
		if (a == b) return;
		//parent[y].key = a;

		if (rank[x] > rank[y])
		{
			parent[y].key = x;
		}
		else
		{
			if (rank[x] == rank[y])
			{
				rank[y]++;
			}
			parent[x].key = y;
		}
	}

private:
	vector<MFSet_struct> parent;
	vector<int> rank;
};

int main()
{
	//构建初始化数组
	vector<MFSet_struct> parent;
	for (int i = 0; i < 9; i++)
	{
		parent.emplace_back(i, i);
	}

	//构建并查集
	MergeFindSet mf(parent);
	int x, y;
	for (int i = 0; i < 6; i++)
	{
		cin >> x >> y;
		mf.merge(x, y);
	}

	/*
	1 3 
	1 2
	5 4
	2 4
	6 8
	8 7
	*/
	cout << (mf.find(2) == mf.find(8) ? "OK" : "NO") << endl;
	cout << (mf.find(2) == mf.find(4) ? "OK" : "NO") << endl;
	cout << (mf.find(3) == mf.find(6) ? "OK" : "NO") << endl;
	cout << (mf.find(1) == mf.find(6) ? "OK" : "NO") << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95