-
45、DVGO
简介
github主页:https://github.com/sunset1995/DirectVoxGO

加速的关键是直接优化在密集体素网格中建模的体积密度。注意,既不需要从任何训练过的隐式模型(如NeRF)转换步骤,也不需要跨场景的预训练,也就是说,体素网格表示是直接有效地从每个场景从头开始训练的贡献点
- 在体素密度直接优化中引入两个先验来避免次优几何
- 提出了后激活体素网格插值,它可以在较低的网格分辨率下实现清晰的边界建模
效果
- 收敛速度比使用NVIDIA RTX 2080 Ti GPU的机器上的nerf减少训练时间(从10 - 20小时到15分钟)快了大约两个数量级
- 以45倍的渲染速度实现了与NeRF相当的视觉质量
- 不需要跨场景的预训练
- 网格分辨率大约是1603,而之前的工作中的网格分辨率在5123到13003之间,以达到与nerf相当的质量
实现流程

NeRF公式回顾
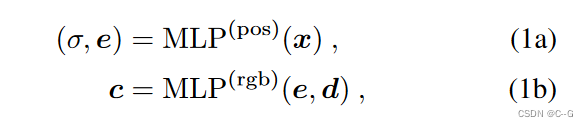

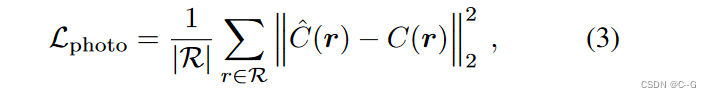
Post-activated density voxel grid
体素网格表示在其网格单元中显式地对感兴趣的形式(例如,密度、颜色或特征)建模。这种显式的场景表示可以有效地通过插值查询任何3D位置
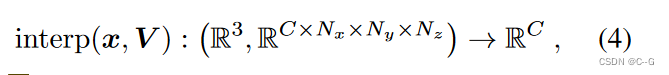
x 为查询的3D点,V 为体素网格,C 为模态维度, N x ⋅ N y ⋅ N z N_x·N_y·N_z Nx⋅Ny⋅Nz为体素总数Density voxel grid for volume rendering
密度体素网格 V ( D e n s i t y ) V^{(Density)} V(Density)是 C = 1的特殊情况,它存储了用于体绘制的密度值
在应用密度激活(即R→R≥0的映射)之前,使用 σ ¨ \ddot{σ} σ¨∈R 表示原始体素密度,使用Mip-NeRF中提到的移位的 softplus 作为密度激活
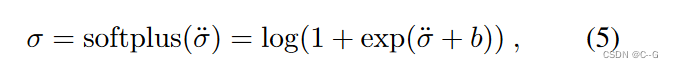
移位 b 是一个超参数,使用softplus代替ReLU是直接优化体素密度的关键,因为当一个体素被错误地设置为负值时,用ReLU作为密度激活是不可挽回的。相反,softplus允许探索非常接近0的密度Sharp decision boundary via post-activation
插值后的体素密度由 softplus (Eq.(5)) 和alpha (Eq. (2b)) 函数依次处理,进行体绘制
给定查询的3D点x,考虑三种不同的顺序——预激活、激活中和激活后——插入三线性插值并执行激活

这里省略深度δ以二维网格单元为例
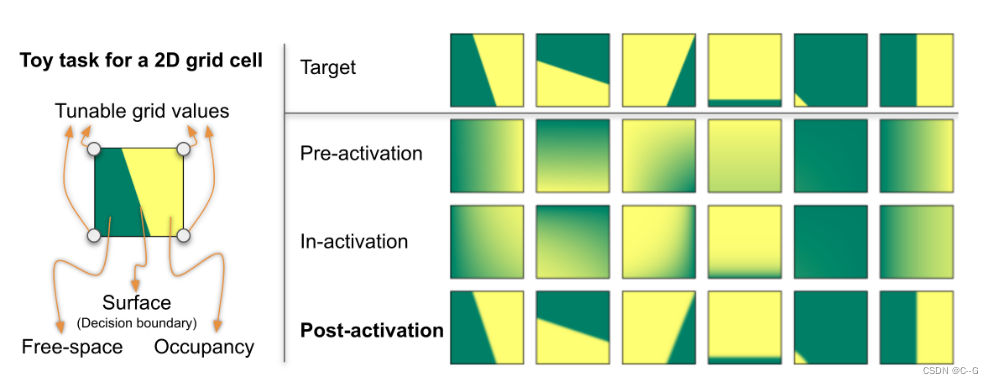
后激活的网格单元可以产生清晰的线性边界,而预激活和失激活的网格单元只能产生平滑的结果,因此需要更多的单元来处理表面细节
网格分辨率 (H/5)× (W/5) 下图像拟合结果的视觉比较。第一行是预激活、中激活和后激活的结果。第二行是它们与目标图像的逐像素绝对差异。
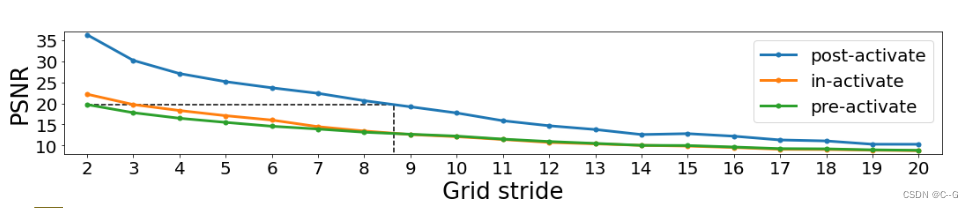
网格步幅s表示网格分辨率为 (H/s) × (W/s)。黑色虚线强调,在本例中,步幅≈8.5 的后激活可以达到与步幅 2 的前激活相同的PSNR上图表明后激活可以获得更好的网格单元的使用效率
Fast and direct voxel grid optimization
Coarse geometry searching

场景主要由空闲空间(即未占用空间)主导,目标是高效地找到感兴趣的粗三维区域,然后重构需要更多计算资源的精细细节和视图依赖效果,这样大大减少后期精细阶段每条射线上查询的点的数量
Coarse scene representation
使用粗密度体素网格 V ( d e n s i t y ) ( c ) ∈ R 1 × N x ( c ) × N y ( c ) × N z ( c ) V^{(density)(c)} ∈ R^{1×N^{(c)}_x×N^{(c)}_y×N^{(c)}_z} V(density)(c)∈R1×Nx(c)×Ny(c)×Nz(c)和后激活来建模场景几何
只在粗阶段用 V ( r g b ) ( c ) ∈ R 3 × N x ( c ) × N y ( c ) × N z ( c ) V^{(rgb)(c)} ∈ R^{3×N^{(c)}_x×N^{(c)}_y×N^{(c)}_z} V(rgb)(c)∈R3×Nx(c)×Ny(c)×Nz(c) 来建模视图不变的颜色发射。对任何3D点x的查询都可以通过插值实现
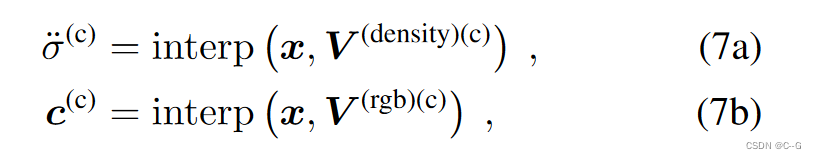
c ( c ) ∈ R 3 c^{(c)}∈R^3 c(c)∈R3为视图不变颜色, σ ¨ ( c ) \ddot{σ}^{(c)} σ¨(c)∈R为原始体积密度Coarse voxels allocation
找到一个包围框(BBox),将训练视图的摄像机截锥紧紧包围起来,设 L x ( c ) , L y ( c ) , L z ( c ) L^{(c)}_x,L^{(c)}_y,L^{(c)}_z Lx(c),Ly(c),Lz(c)为BBox的长度, M ( x ) M^{(x)} M(x)为粗阶段期望体素总数的超参数,则体素大小为 s ( c ) = L x ( c ) ⋅ L y ( c ) ⋅ L z ( c ) 3 s^{(c)} = \sqrt[3]{L^{(c)}_x·L^{(c)}_y·L^{(c)}_z} s(c)=3Lx(c)⋅Ly(c)⋅Lz(c),即BBox的每条边为 N x ( c ) , N y ( c ) , N z ( c ) = ⌊ L x ( c ) / s ( c ) ⌋ , ⌊ L y ( c ) / s ( c ) ⌋ , ⌊ L z ( c ) / s ( c ) ⌋ N^{(c)}_x,N^{(c)}_y,N^{(c)}_z = \lfloor L^{(c)}_x / s^{(c)} \rfloor,\lfloor L^{(c)}_y / s^{(c)} \rfloor,\lfloor L^{(c)}_z / s^{(c)} \rfloor Nx(c),Ny(c),Nz(c)=⌊Lx(c)/s(c)⌋,⌊Ly(c)/s(c)⌋,⌊Lz(c)/s(c)⌋
Coarse-stage points sampling
像素渲染射线上,将查询点抽样为

o为相机中心,d为光线投射方向, t ( n e a r ) t^{(near)} t(near)为相机近界, δ ( c ) δ^{(c)} δ(c)为步长超参数,根据体素大小 s ( c ) s^{(c)} s(c) 自适应选择步长.查询索引 i 的范围从 ⌈ t ( f a r ) ⋅ ∣ ∣ d ∣ ∣ 2 / δ ( c ) ⌉ \lceil t^{(far)} · ||d||^2 / δ^{(c)} \rceil ⌈t(far)⋅∣∣d∣∣2/δ(c)⌉ ,其中 t ( f a r ) t^{(far)} t(far)是摄像机远界,因此最后一个采样点停止在远面附近
先验1:low-density initialization
在训练开始时,由于Eq. (2c)中的累计透射率项,远离摄像机的点的重要性被降低,粗密度体素网格 V ( d e n s i t y ) ( c ) V^{(density)(c)} V(density)(c) 可能会意外地被困在一个次优的“混浊”几何,在相机附近的平面密度更高。因此,必须更仔细地初始化 V ( d e n s i t y ) ( c ) V^{(density)(c)} V(density)(c) ,以确保在一开始光线上的所有采样点对相机都是可见的,即,Eq. (2c)中的累计透射率 T i s T_is Tis 接近于1
将 V ( d e n s i t y ) ( c ) V^{(density)(c)} V(density)(c) 中的所有网格值初始化为0,并将Eq.(5)中的偏差项设为
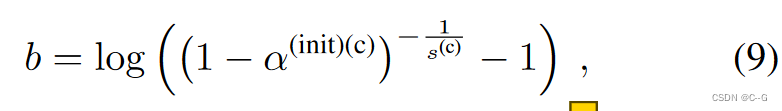
α ( i n i t ) ( c ) α^{(init)(c)} α(init)(c)是一个超参数,对于一个长度为 s ( c ) s^{(c)} s(c) 的体素距离的射线,累积透射率 T i T_i Ti 衰减 1− α ( i n i t ) ( c ) α^{(init)(c)} α(init)(c)≈1先验2:view-count-based learning rate
在现实世界捕获中,可能会有一些体素只在少量的训练视图可见,而我们更需要在许多视图中具有一致性的表面,而不是只能解释少数视图的表面。在实际操作中,对 V ( d e n s i t y ) ( c ) V^{(density)(c)} V(density)(c) 中不同的网格点设置了不同的学习率。对于每个用 j 索引的网格点,我们计算 j 可见点的训练视图数量 n j n_j nj,然后按 n j / n m a x n_j / n_max nj/nmax 缩放其基本学习速率,其中 n m a x n_max nmax 是所有网格点的最大视图计数。
Training objective for coarse representation
通过最小化渲染颜色和观察颜色之间的均方误差来重建场景表示。为了正则化重建,主要利用背景熵损失来鼓励累积的alpha值集中在背景或前景上
Fine detail reconstruction
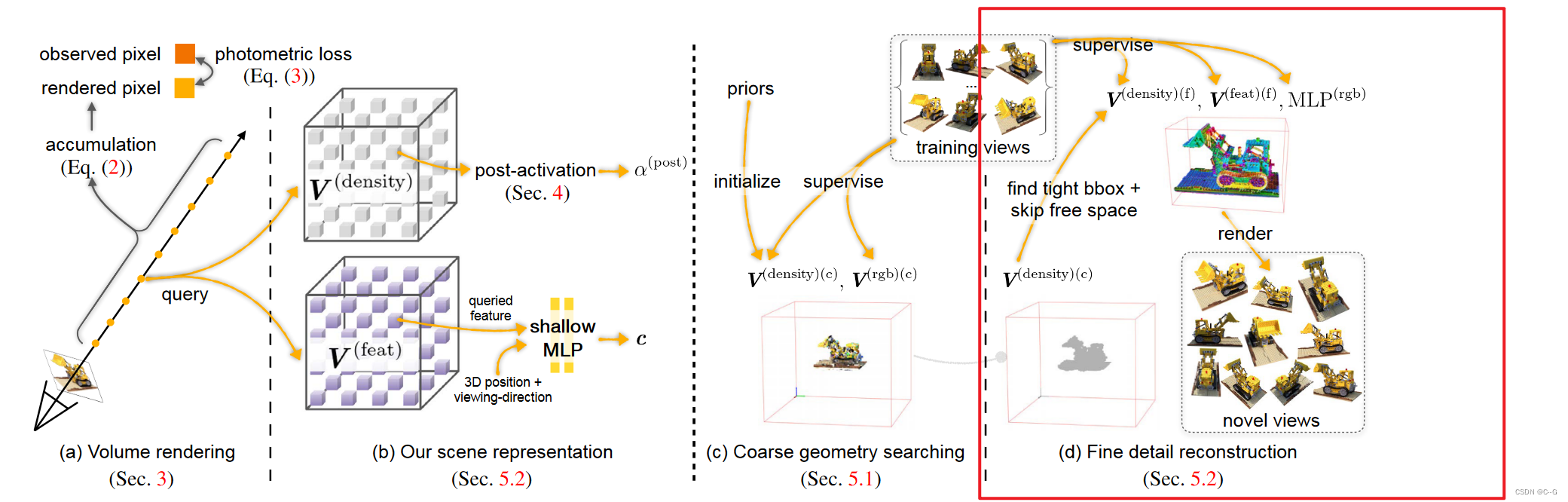
优化后的 V ( d e n s i t y ) ( c ) V^{(density)(c)} V(density)(c) 在此阶段被冻结
Fine scene representation
在精细阶段,使用高分辨率密度体素网格 V ( d e n s i t y ) ( f ) ∈ R 1 × N x ( f ) × N y ( f ) × N z ( f ) V^{(density)(f)} ∈ R^{1×N^{(f)}_x×N^{(f)}_y×N^{(f)}_z} V(density)(f)∈R1×Nx(f)×Ny(f)×Nz(f),并进行后激活插值(Eq. (6c))
为了建模与视图相关的颜色发射,选择使用一种显式-隐式混合表示,实验发现,显式表示往往产生较差的结果,而隐式表示需要较慢的训练速度
为此,论文采用混合表示
- 特征体素网格 V ( f e a t ) ( f ) ∈ R D × N x ( f ) × N y ( f ) × N z ( f ) V^{(feat)(f)} ∈ R^{D×N^{(f)}_x×N^{(f)}_y×N^{(f)}_z} V(feat)(f)∈RD×Nx(f)×Ny(f)×Nz(f),其中D是特征空间维的超参数
- 由Θ参数化的浅MLP
- 在此阶段对3D点 x 和观看方向 d 进行查询
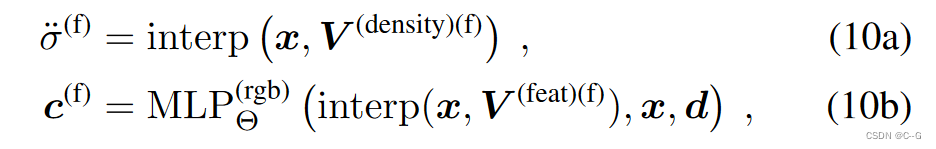
其中 c ( f ) ∈ R 3 c^{(f)}∈R^3 c(f)∈R3 为视相关的颜色发射, σ ¨ ( f ) \ddot{σ}^{(f)} σ¨(f)∈R为精细阶段的原始体积密度。位置嵌入应用于 x, d 对于 M L P Θ ( r g b ) MLP^{(rgb)}_Θ MLPΘ(rgb)。
Known free space and unknown space
如果优化 V ( d e n s i t y ) ( c ) V^{(density)(c)} V(density)(c) 的后激活alpha值小于阈值 τ ( c ) τ^(c) τ(c),则查询点位于已知空闲空间。否则,称查询点位于未知空间
Fine voxels allocation
密集查询 V ( d e n s i t y ) ( c ) V^{(density)(c)} V(density)(c)以找到一个紧紧包围未知空间的BBox,其中 L x ( f ) , L y ( f ) , L z ( f ) L^{(f)}_x,L^{(f)}_y,L^{(f)}_z Lx(f),Ly(f),Lz(f) 是BBox的长度。唯一的超参数是体素的期望总数 M ( f ) M^{(f)} M(f)。体素大小 s ( f ) s^{(f)} s(f) 和网格尺寸 N x ( f ) , N y ( f ) , N z ( f ) N^{(f)}_x,N^{(f)}_y,N^{(f)}_z Nx(f),Ny(f),Nz(f)可以从 M ( f ) M^{(f)} M(f)自动导出。
Progressive scaling
受NSVF的启发,逐步扩展体素网格 V ( d e n s i t y ) ( f ) V^{(density)(f)} V(density)(f) 和 V ( f e a t ) ( f ) V^{(feat)(f)} V(feat)(f)。设pg_ckpt为检查点步骤集。体素的初始数量设置为 ⌊ M ( f ) / 2 ∣ p g _ c k p t ∣ ⌋ \lfloor M^{(f)} / 2^{|pg\_ckpt|} \rfloor ⌊M(f)/2∣pg_ckpt∣⌋ 。当到达pg_ckpt中的训练步骤时,将体素数量加倍,使最后一个检查点后的体素数量为 M ( f ) M^{(f)} M(f);相应地更新体素大小 s ( f ) s^{(f)} s(f) 和网格尺寸 N x ( f ) , N y ( f ) , N z ( f ) N^{(f)}_x,N^{(f)}_y,N^{(f)}_z Nx(f),Ny(f),Nz(f)。缩放场景表示要简单得多。在每个检查点,通过三线性插值调整体素网格 V ( d e n s i t y ) ( f ) V^{(density)(f)} V(density)(f) 和 V ( f e a t ) ( f ) V^{(feat)(f)} V(feat)(f)
Fine-stage points sampling
点采样策略与式(8)相似,但做了一些修改。首先过滤掉不与已知自由空间相交的射线。对于每条射线,调整近界和远界 t ( n e a r ) t^{(near)} t(near)和远界 t ( f a r ) t^{(far)} t(far) 到射线盒交点的两个端点。如果 x 0 x_0 x0已经在BBox中,我们不调整 t ( n e a r ) t^{(near)} t(near)。
Free space skipping
查询 V ( d e n s i t y ) ( c ) V^{(density)(c)} V(density)(c) (Eq. (7a))比查询 V ( d e n s i t y ) ( f ) V^{(density)(f)} V(density)(f)(Eq. (10a))快;查询与视图相关的颜色(Eq. (10b))是最慢的。通过在训练和测试中自由跳过空间来提高细阶段效率。首先,通过检查优化的 V ( d e n s i t y ) ( c ) V^{(density)(c)} V(density)(c)(Eq. (7a)),跳过已知空闲空间中的采样点。其次,通过查询 V ( d e n s i t y ) ( f ) V^{(density)(f)} V(density)(f) (Eq. (10a)),进一步跳过激活alpha值较低的未知空间中的采样点( τ ( f ) τ^{(f)} τ(f)处的阈值)。
Training objective for fine representation
使用与粗阶段相同的训练损失,但使用更小的权值作为正则化损失,因为,根据经验,它会带来略好的质量。
Implementation details
实际测试中,设置 M ( c ) = 10 0 3 M^{(c)} = 100^3 M(c)=1003, M ( f ) = 16 0 3 M^{(f)} = 160^3 M(f)=1603
a ( i n i t ) ( c ) = 1 0 − 6 a^{(init)(c)} = 10^{-6} a(init)(c)=10−6,使用较高的 α ( i n i t ) ( f ) = 1 0 − 2 α^{(init)(f)} = 10^{−2} α(init)(f)=10−2,因为查询点集中在精阶段优化的粗几何上。
点采样步长设置为体素大小的一半,即 δ ( c ) = 0.5 ⋅ s ( c ) a n d δ ( f ) = 0.5 ⋅ s ( f ) δ^{(c)} = 0.5 · s^{(c)} and δ^{(f)} = 0.5 · s^{(f)} δ(c)=0.5⋅s(c)andδ(f)=0.5⋅s(f)
浅层MLP包含两个隐藏层,共128个通道
效果

-
相关阅读:
【C语言必知必会| 第十篇】指针入门,这一篇就够了
线性表的链式存储结构——链表
JoySSL证书买二送一买三送二特别活动
基于ssm的社区医院儿童预防接种管理系统设计与实现-计算机毕业设计源码+LW文档
NLP中token总结
windows10系统安装nvm切换电脑node版本
Linux—-vim基础使用
【好书推荐】如何快速入门短视频?带你3天成为短视频与Vlog剪辑高手
类的构造函数执行顺序
导出execl,后端接口返回文件流
- 原文地址:https://blog.csdn.net/weixin_50973728/article/details/126922818