分类器的不确定度估计

分类器的不确定度估计

不确定度估计，即置信程度。

通俗地讲，就是目前模型预测结果正确的概率。

sklearn中有两个函数可以用于获取分类器的不确定度估计，分别为 decision_function 和 predict_proba 两个函数。

决策函数(decision_function)

decision_function，即为决策函数。

对于二分类的情况，decision_function返回值的形状为(n_samples,)，它只可以估计正类的概率(对于二分类情况来说，‘反’类始终是classes_属性的第一个元素，‘正’类是classes_属性的第二个元素)，如果是正值，越大表示对‘正’类的置信度越高，如果为‘负’值，其绝对值越大表示对‘负’类的置信度越高。

示例

以下是简单的示例:

import numpy as np
from sklearn.ensemble import GradientBoostingClassifier                  #梯度提升决策树分类器
from sklearn.datasets import make_circles                                #引入数据集
from sklearn.model_selection import train_test_split                     #引入数据集分割函数

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)               #获取数据集

#为了便于说明，将两个类别重命名为'blue'、'red'
y_named = np.array(['blue','red'])[y]                                     #使用numpy的方式直接进行重命名

#我们可以对任意个数组调用train_test_split
#所有数组的划分方式都是一致的
X_train, X_test, y_train_named, y_test_named, y_train, y_test = \
    train_test_split(X, y_named, y, random_state=0)

#构建梯度提升模型
gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train, y_train_named)                                           #训练数据


print('X_test.shape:{}'.format(X_test.shape))                                            #输出X_test测试集的形状
print('Decision function shape:{}'.format(grbt.decision_function(X_test).shape))         #输出决策函数进行预测的情况

print('Decision function data:{}'.format(grbt.decision_function(X_test)))                #输出每个预测值的置信度
print('Predict result:{}'.format(grbt.predict(X_test)))                                  #输出每个样本的预测结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

X_test.shape:(25, 2)
Decision function shape:(25,)
Decision function data:[ 4.13592603 -1.70169917 -3.95106099 -3.62609552  4.28986642  3.66166081
 -7.69097179  4.11001686  1.10753937  3.40782222 -6.46255955  4.28986642
  3.90156346 -1.20031247  3.66166081 -4.17231157 -1.23010079 -3.91576223
  4.03602783  4.11001686  4.11001686  0.65709014  2.69826265 -2.65673274
 -1.86776596]
Predict result:['red' 'blue' 'blue' 'blue' 'red' 'red' 'blue' 'red' 'red' 'red' 'blue'
 'red' 'red' 'blue' 'red' 'blue' 'blue' 'blue' 'red' 'red' 'red' 'red'
 'red' 'blue' 'blue']
1
2
3
4
5
6
7
8
9
10

我们可以对比一下置信度与预测结果的对照是否一致

#先将所有置信度转化为布尔类型数据
gbrt.decision_function(X_test) > 0                      #置信结果大于0，即为正类，否则为负类
1
2

array([ True, False, False, False,  True,  True, False,  True,  True,
        True, False,  True,  True, False,  True, False, False, False,
        True,  True,  True,  True,  True, False, False])
1
2
3

如果返回 True，代表的是正类(red)；返回的是False，代表的是负类(blue)。下面将这些布尔值转化为0或1。

greater_zero = (gbrt.decision_function(X_test)>0).astype(int)              #将布尔值True/False转化为1或0
pred = gbrt.classes_[greater_zero]                                         #利用0和1作为classes的索引

print(pred)                                                                #输出由决策边界置信度得到的结果
print(gbrt.predict(X_test))                                               #输出结果

print('pred is equal to predictions:{}'.\
      format(np.all(pred == gbrt.predict(X_test))))                        #pred与gbrt.predict的输出完全相同
1
2
3
4
5
6
7
8

['red' 'blue' 'blue' 'blue' 'red' 'red' 'blue' 'red' 'red' 'red' 'blue'
 'red' 'red' 'blue' 'red' 'blue' 'blue' 'blue' 'red' 'red' 'red' 'red'
 'red' 'blue' 'blue']
['red' 'blue' 'blue' 'blue' 'red' 'red' 'blue' 'red' 'red' 'red' 'blue'
 'red' 'red' 'blue' 'red' 'blue' 'blue' 'blue' 'red' 'red' 'red' 'red'
 'red' 'blue' 'blue']
pred is equal to predictions:True
1
2
3
4
5
6
7

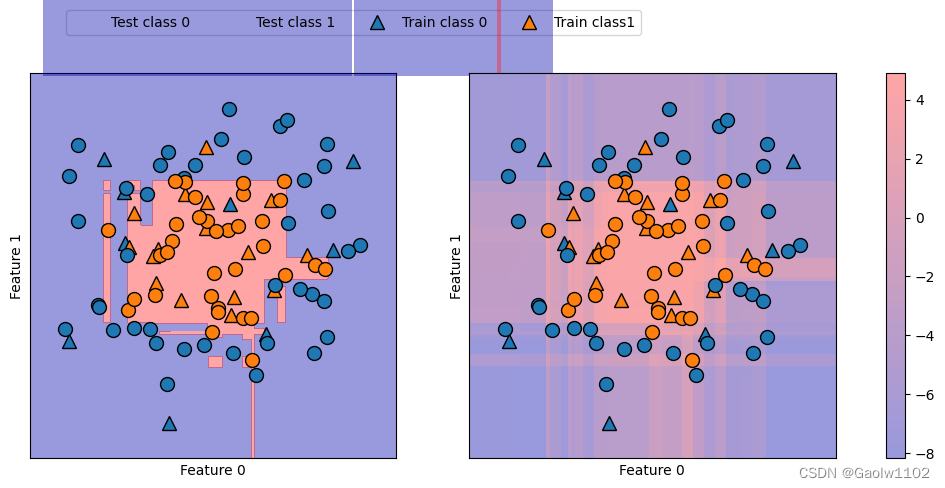
决策函数置信度与预测结果的关系(图像)

在下面的例子中，我们利用颜色编码在二维平面中画出所有点的decision_function, 还有决策边界。

其中训练点为圆点，测试数据为三角形。

import matplotlib.pyplot as plt                               #引入绘图库
import mglearn                                                #引入mglearn库

fig, axes = plt.subplots(1, 2, figsize=(13,5))                 #定义绘图面板

mglearn.tools.plot_2d_separator(gbrt, X, ax=axes[0],                          #绘制决策函数分界线
                               alpha=.4, fill=True, cm=mglearn.cm2)
scores_image = mglearn.tools.plot_2d_scores(gbrt, X, ax=axes[1],
                                           alpha=.4, cm=mglearn.ReBl)         #绘制置信值图形

#绘制所有的数据样本
for ax in axes:
    
    mglearn.discrete_scatter(X_test[:,0], X_test[:,1], y_test,
                            markers='^', ax=ax)                               #绘制测试集的数据点
    mglearn.discrete_scatter(X_train[:,0], X_train[:,1], y_train,
                            markers='o', ax=ax)                               #绘制训练集的数据点

    ax.set_xlabel('Feature 0')
    ax.set_ylabel('Feature 1')                                 #添加特征名称

cbar = plt.colorbar(scores_image, ax=axes.tolist())            #绘制颜色bar
axes[0].legend(['Test class 0', 'Test class 1',
                 'Train class 0', 'Train class1'], ncol=4, loc=(.1, 1.1))       #添加标签
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

1

预测概率(predict_proba)

predict_proba的输出是每个类别的概率，往往更容易理解。

对于二分类问题，它的形状往往为(n_samples, 2)。现在试着输出一下上例每类别的概率:

示例

import numpy as np
from sklearn.ensemble import GradientBoostingClassifier                  #梯度提升决策树分类器
from sklearn.datasets import make_circles                                #引入数据集
from sklearn.model_selection import train_test_split                     #引入数据集分割函数

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)               #获取数据集

#为了便于说明，将两个类别重命名为'blue'、'red'
y_named = np.array(['blue','red'])[y]                                     #使用numpy的方式直接进行重命名

#我们可以对任意个数组调用train_test_split
#所有数组的划分方式都是一致的
X_train, X_test, y_train_named, y_test_named, y_train, y_test = \
    train_test_split(X, y_named, y, random_state=0)

#构建梯度提升模型
gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train, y_train_named)                                           #训练数据


print('X_test.shape:{}'.format(X_test.shape))                                            #输出X_test测试集的形状
print('Predict_proba shape:{}'.format(grbt.predict_proba(X_test).shape))                 #输出置信度预测概率的情况

print('Predict_proba data:\n',grbt.predict_proba(X_test))                                #输出每个预测值的置信度
print('Predict result:{}'.format(grbt.predict(X_test)))                                  #输出每个样本的预测结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

X_test.shape:(25, 2)
Predict_proba shape:(25, 2)
Predict_proba data:
 [[1.57362639e-02 9.84263736e-01]
 [8.45756526e-01 1.54243474e-01]
 [9.81128693e-01 1.88713075e-02]
 [9.74070327e-01 2.59296728e-02]
 [1.35214212e-02 9.86478579e-01]
 [2.50463747e-02 9.74953625e-01]
 [9.99543275e-01 4.56725221e-04]
 [1.61426376e-02 9.83857362e-01]
 [2.48329911e-01 7.51670089e-01]
 [3.20518935e-02 9.67948107e-01]
 [9.98441637e-01 1.55836338e-03]
 [1.35214212e-02 9.86478579e-01]
 [1.98099245e-02 9.80190075e-01]
 [7.68580365e-01 2.31419635e-01]
 [2.50463747e-02 9.74953625e-01]
 [9.84817480e-01 1.51825198e-02]
 [7.73836215e-01 2.26163785e-01]
 [9.80463909e-01 1.95360915e-02]
 [1.73607896e-02 9.82639210e-01]
 [1.61426376e-02 9.83857362e-01]
 [1.61426376e-02 9.83857362e-01]
 [3.41393574e-01 6.58606426e-01]
 [6.30759509e-02 9.36924049e-01]
 [9.34424749e-01 6.55752512e-02]
 [8.66199569e-01 1.33800431e-01]]
Predict result:['red' 'blue' 'blue' 'blue' 'red' 'red' 'blue' 'red' 'red' 'red' 'blue'
 'red' 'red' 'blue' 'red' 'blue' 'blue' 'blue' 'red' 'red' 'red' 'red'
 'red' 'blue' 'blue']
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

其中，每行的第一个元素是第一个类别的估计概率，第二个元素是第二个类别的估计概率。

由于predict_proba的输出是一个概率，因此总是在0和1之间，这两个类别元素之和始终为1，当有一个类别的概率超50%，该类别即模型的预测结果。

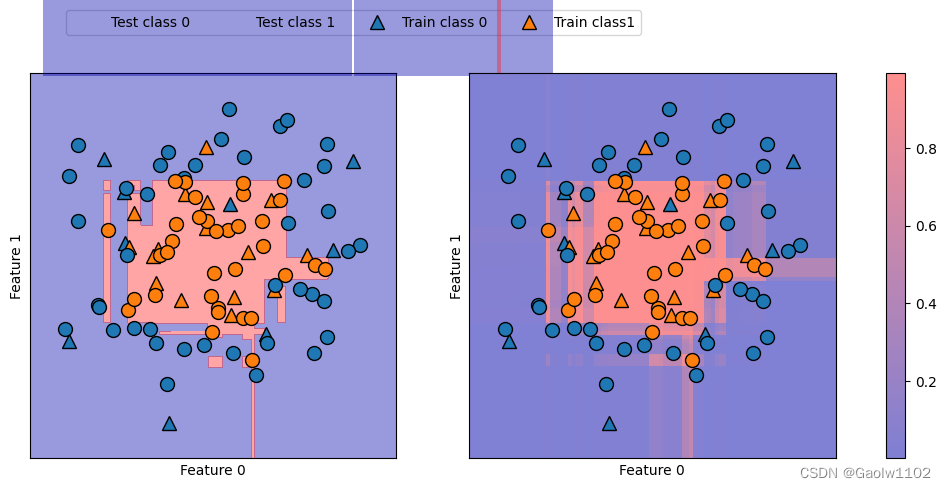
预测概率与预测结果的关系(图像)

同样的，再次给出该数据集的决策边界，以及类别1的类别概率

import matplotlib.pyplot as plt                               #引入绘图库
import mglearn                                                #引入mglearn库

fig, axes = plt.subplots(1, 2, figsize=(13,5))                 #定义绘图面板

mglearn.tools.plot_2d_separator(gbrt, X, ax=axes[0],                          #绘制决策函数分界线
                               alpha=.4, fill=True, cm=mglearn.cm2)
scores_image = mglearn.tools.plot_2d_scores(gbrt, X, ax=axes[1],
                                           alpha=.5, cm=mglearn.ReBl,
                                           function='predict_proba')          #绘制置信值图形

#绘制所有的数据样本
for ax in axes:
    
    mglearn.discrete_scatter(X_test[:,0], X_test[:,1], y_test,
                            markers='^', ax=ax)                               #绘制测试集的数据点
    mglearn.discrete_scatter(X_train[:,0], X_train[:,1], y_train,
                            markers='o', ax=ax)                               #绘制训练集的数据点

    ax.set_xlabel('Feature 0')
    ax.set_ylabel('Feature 1')                                 #添加特征名称

cbar = plt.colorbar(scores_image, ax=axes.tolist())            #绘制颜色bar
axes[0].legend(['Test class 0', 'Test class 1',
                 'Train class 0', 'Train class1'], ncol=4, loc=(.1, 1.1))       #添加标签
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

1

多分类问题的不确定度

之前仅讨论了二分类问题中的不确定度估计，但decision_function和predict_proba也适用于多分类问题。

现在将这两个函数应用于鸢尾花数据集，该数据集是一个三分类数据集

决策函数多分类问题的不确定度

先看下面的例子:

from sklearn.datasets import load_iris              #引入鸢尾花数据集

iris = load_iris()                                   #加载鸢尾花数据集
X_train, X_test, y_train, y_test = \
    train_test_split(iris.data, iris.target,
                     random_state=42)                #切分数据集

#构造梯度提升决策树
gbrt = GradientBoostingClassifier(learning_rate=0.01,
                                   random_state=0)

gbrt.fit(X_train, y_train)                           #训练数据集


#输出决策函数预测后的形状
print('Decision function shape:{}'.format(gbrt.decision_function(X_test).shape))
print('Decision function:\n{}'.format(gbrt.decision_function(X_test)[:6,:]))             #输出前6挑数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Decision function shape:(38, 3)
Decision function:
[[-1.995715    0.04758267 -1.92720695]
 [ 0.06146394 -1.90755736 -1.92793758]
 [-1.99058203 -1.87637861  0.09686725]
 [-1.995715    0.04758267 -1.92720695]
 [-1.99730159 -0.13469108 -1.20341483]
 [ 0.06146394 -1.90755736 -1.92793758]]
1
2
3
4
5
6
7
8

对于多分类的情况，decision_function的形状为(n_samples, n_classes)，每一列对应每个类别的 “确定度分数” 。

分数较高的类别可能性更大，分数较低的类别可能性较小。 可以找出每个数据点的最大元素，利用最大元素来再现预测结果:

print('Argmax of decision function:\n{}'.format(np.argmax(
    gbrt.decision_function(X_test), axis=1)))                          #取出每一行的最大元素对应的下标
print('Prediciton:\n{}'.format(gbrt.predict(X_test)))                   #输出预测结果


1
2
3
4
5

Argmax of decision function:
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1
 0]
Prediciton:
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1
 0]
1
2
3
4
5
6

预测概率多分类问题的不确定度

先看如下例子:

from sklearn.datasets import load_iris              #引入鸢尾花数据集

iris = load_iris()                                   #加载鸢尾花数据集
X_train, X_test, y_train, y_test = \
    train_test_split(iris.data, iris.target,
                     random_state=42)                #切分数据集

#构造梯度提升决策树
gbrt = GradientBoostingClassifier(learning_rate=0.01,
                                   random_state=0)

gbrt.fit(X_train, y_train)                           #训练数据集


#输出决策函数预测后的形状
print('predict_proba shape:{}'.format(gbrt.predict_proba(X_test).shape))
print('predict_proba:\n{}'.format(gbrt.predict_proba(X_test)[:6,:]))             #输出前6挑数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

predict_proba shape:(38, 3)
predict_proba:
[[0.10217718 0.78840034 0.10942248]
 [0.78347147 0.10936745 0.10716108]
 [0.09818072 0.11005864 0.79176065]
 [0.10217718 0.78840034 0.10942248]
 [0.10360005 0.66723901 0.22916094]
 [0.78347147 0.10936745 0.10716108]]
1
2
3
4
5
6
7
8

可以发现，多分类问题下预测概率函数predict_proba的置信度同二分类问题是一致的。

形状为(n_samples, n_classes)。 其中每个数据点的所有可能类别的概率之和为 1。

同样的，也可以采用这种方式来预测结果:

print('Argmax of predict_proba:\n{}'.format(np.argmax(
    gbrt.decision_function(X_test), axis=1)))                          #取出每一行的最大元素对应的下标
print('Prediciton:\n{}'.format(gbrt.predict(X_test)))                   #输出预测结果
1
2
3

Argmax of predict_proba:
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1
 0]
Prediciton:
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1
 0]
1
2
3
4
5
6

这里一定要注意，如果类别为字符串或者其它整数时，必须使用分类器classes_属性获取真实属性名称才可进行对比。