Python实现基于DFS和BFS算法的吃豆人寻路实验

吃豆人寻路实验

一、实现 DFS 和 BFS

要优化之前首先要完成最基本的版本，因此首先完成了最基础的 dfs 和 bfs 的算法，算法的流程如下图：

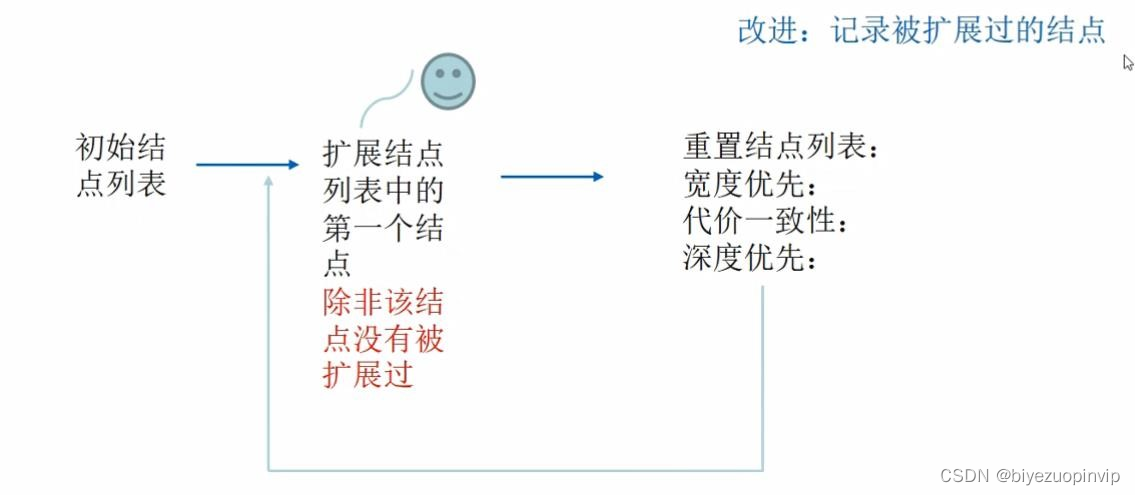
在这里插入图片描述

图 1 算法流程需要注意的是，dfs 扩展节点的时候会把节点放在队列首位，并在下次立刻取出；bfs 则会把节点放在队列尾部，并且当前面的遍历完后才会取出，分别对应的是“先入后出”和“先入先出”，因此使用的数据结构分别是“栈”和“队列”。

1.1 伪代码

接下来展示 dfs 和 bfs 在该问题中的伪代码：	接下来展示 dfs 和 bfs 在该问题中的伪代码：	接下来展示 dfs 和 bfs 在该问题中的伪代码：
1.1.1 DFS 伪代码	1.1.2 BFS 伪代码	1.1.2 BFS 伪代码
定义 DFS 栈	定义 BFS 队列	定义 BFS 队列
定义结果栈	定义父亲节点字典	定义父亲节点字典
将起点放入栈		将起点放入队列
While 栈非空：		While 队列非空：
取出栈顶节点，再放入		取出队列头节点，并删掉
标记该点被访问		标记该点被访问
If 到达终点：		If 到达终点：
返回结果栈		根据字典，返回结果
对该节点进行扩展		对该节点进行扩展
For 每个扩展节点：		For 每个扩展节点：
If 扩展节点没被访问：		If 扩展节点没被访问：
入栈顶； If 该节点没有扩展节点: ； DFS 栈中删除该节点结果栈中删除该节点		入队尾

1.2 结果展示

分别对 dfs 和 bfs 进行测试，可以得到下面的结果

1.2.1 DFS扩展结果

在这里插入图片描述

图 1 普通 dfs 小地图

在这里插入图片描述

图 2 普通 dfs 中地图

在这里插入图片描述

图 3 普通 dfs 大地图

1.2.2 BFS扩展结果

在这里插入图片描述

图 4 普通 bfs 小地图

在这里插入图片描述

图 5 普通 bfs 中地图

在这里插入图片描述

图 6 普通 bfs 大地图

接下来是地图遍历过程的展示

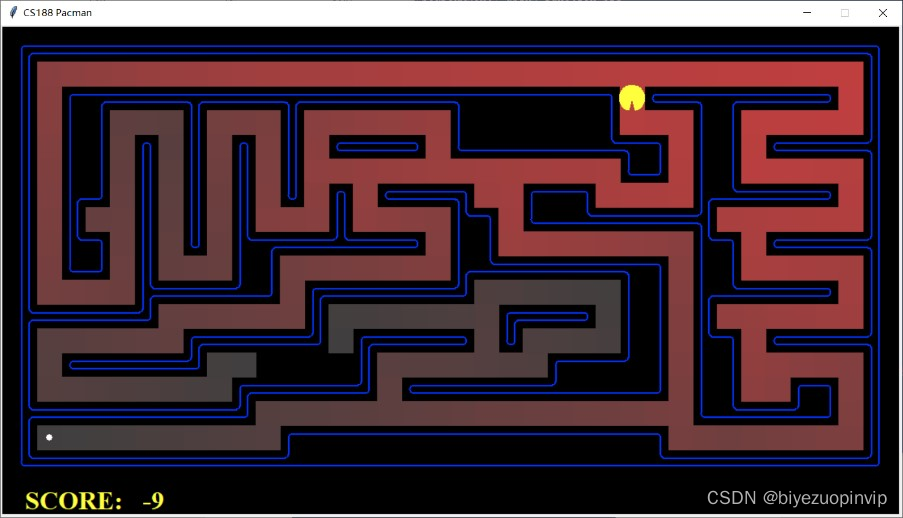
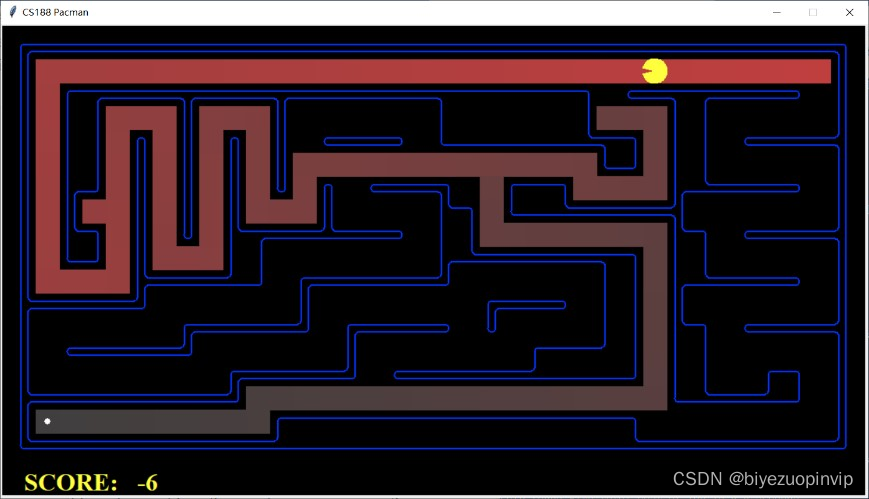
在这里插入图片描述

1.2.3 地图展示：

图 7 地图可视化结果

上图展示的地图结果，左边都是 dfs 的搜索方式，右边都是 bfs 的搜索方式，可以看到 dfs 的搜索策略经常是一条路走到黑，直到找到终点。而 bfs 会搜索全部可以到达的地点，直到找到终点。

这里需要说明的是，无论是 dfs 还是 bfs 我都只是单纯的设置“找到终点后就退出”，因此没有遍历完全部的路径，因为从道理上来说，dfs 和 bfs 的搜索方式都属于全部搜索的暴力式搜索，理应搜索出全部能到达终点的路径，并存起来，判断得到最优路径的。

二、对算法进行优化

在优化的过程中我询问了 111172 班的汪圣翔关于 DFS 优化的问题，最终达成共识 DFS 似乎没法进行优化…我的理解是这样的：由于 DFS 的定义是在每次扩展的时候，直接对第一个被扩展到的节点进行向下搜索，因此 DFS 没有选择的余地。而对于 BFS 来说，它会列出所有被扩展到的节点，这样一来，就有了使用评价函数进行优化的余地了，可以在这一步对节点进行排序，将评价更高的节点进行扩展，这样就能比原来更快地找到到达终点的路径。

我一共写了三种优化方式，分别是贪心和 A*，用到了 util 中提供的优先队列的定义。这里只需要将各自的评价函数进行定义，就可以得到符合该算法的优先队列了，我的函数定义如下：

在这里插入图片描述

图 8 启发式函数以及优先队列的定义，由于是在 DFS 的函数里面写的这个算法，因此变量名沿用了 dfs_stack 这个叫法将启发函数定义翻译成中文，如下：

贪心：从该节点到终点的曼哈顿距离 A*：从该节点到终点的曼哈顿距离 + 从该节点到起点的曼哈顿距离接下来是三种优化的结果展示，如下图所示：

2.1 贪心优化

在这里插入图片描述

图 8 贪心优化中地图

在这里插入图片描述

图 9 贪心优化大地图

2.2 *优化

在这里插入图片描述

图 10 A*优化中地图

相关阅读:
动态域名解析
 Kubernetes(k8s)上搭建一主两从的mysql8集群
 前端面试题JavaScript篇——2022-09-22
OPT锂电池极耳缺陷检测方案
 解决问题：Replace `‘vue‘；⏎` with `“vue“；`
国内AI大赛汇总
 Tensorflow简单CNN实现
 React-hooks有哪些包括用法是什么？
k8s教程（14）-pod之node亲和性调度
 JADE盲分离算法仿真
原文地址：https://blog.csdn.net/newlw/article/details/126907573