基于极化码（Polar Code)的加密

一. 历史背景

香农曾提出，在任何信道上，可信通信的要求如下：

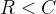
上式子中R代表码率，C代表信道容量。其中码率的计算公式如下：

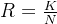
上式子中K代表码字长度，N代表总长度。Erdal Arikan第一个发现能实现此目标的人：极化码。此处先放一张极化码很典型的一张图：

二.信道传输介绍

利用X代表二进制输入（通常为0或1），Y代表输出，W(y|x)代表转移概率，W代表离散无记忆的信道，由此可计算信道容量如下：

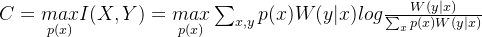
在传递信息时，通常有两种，第一种二进制对称信道的传递规则如下：

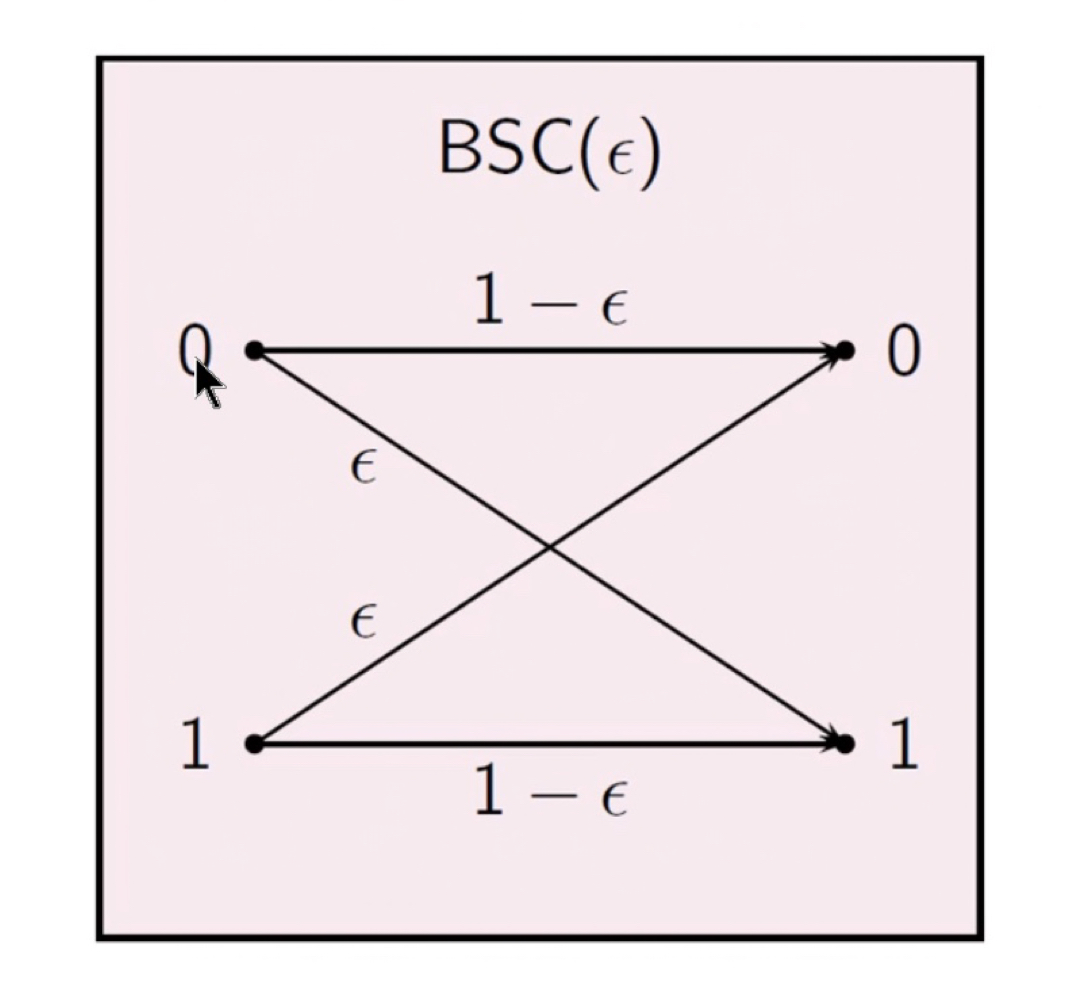
由此可得到转移概率矩阵如下：

\begin{bmatrix}1-\epsilon&\epsilon\\ \epsilon&1-\epsilon \end{}" role="presentation" style="position: relative;">\begin{bmatrix}1-\epsilon&\epsilon\\ \epsilon&1-\epsilon \end{}$\text{begin{bmatrix}1-epsilon\&epsilon epsilon\&1-epsilon end{}}$

第二种是二进制擦除信道，此时的传递图如下：
 

由此类似得到的转移概率矩阵如下：

\begin{bmatrix}1-\epsilon&\epsilon&0\\0&\epsilon&1-\epsilon \end{}" role="presentation" style="position: relative;">\begin{bmatrix}1-\epsilon&\epsilon&0\\0&\epsilon&1-\epsilon \end{}$\text{begin{bmatrix}1-epsilon\&epsilon\&00\&epsilon\&1-epsilon end{}}$

将信道特殊为输出-输出对称信道，由此上述的信道容量公式可进一步化简为如下：

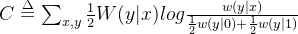
不难得出信道容量的取值范围如下：

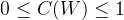
考虑两种极端情况，完美信道定义如下：

无用信道定义如下：

极化码的目的就是将普通的信道W，往这两个极端进行极化。

三.极化过程分析

将一个W信道复用为两个，如下：

 其中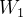信道的互信息分析如下：

类似，信道的互信息分析如下：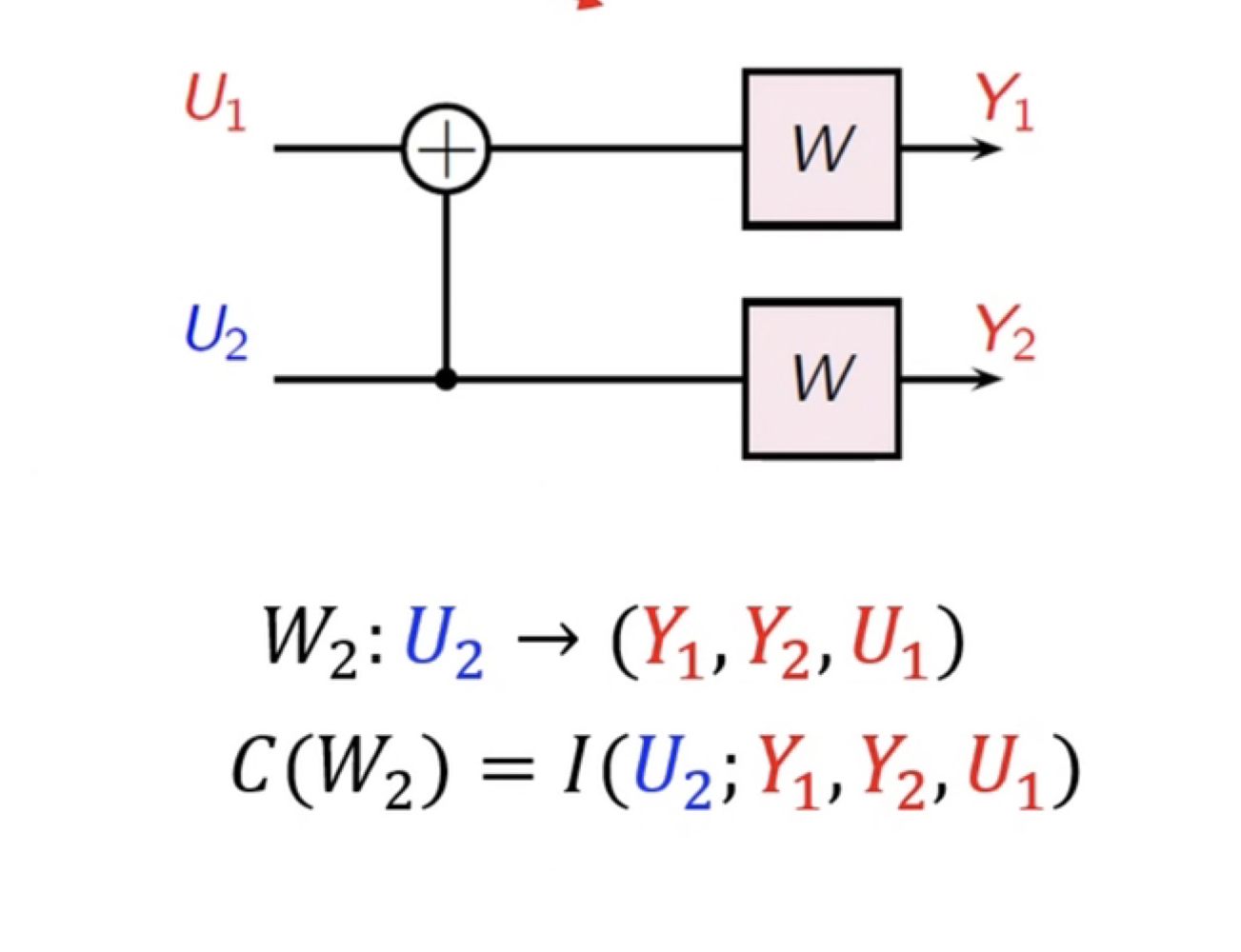

依据互信息的链式法则，如下：

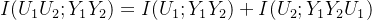
借助信道守恒法则，如下：

最终可得第一次极化的结果如下：

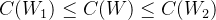
将二输入增加为四输入，如下图：

由此经过多次极化后，结果如下：

四.例题分析

设定信道为二进制擦除信道且概率为0.5，也就是W=BEC(0.5)，N=8，Rate=0.5，可自行设定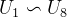的取值分析以下例题的输出。

 

五.基于极化码的密码系统

此处将以McEliece举例进行分析。

5.1 密钥生成算法

设定纠错容量与t相关，G代表转移矩阵，P代表相关概率，由此可得私钥如下：

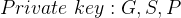
将以上三个元素进行相乘得到公钥，如下：

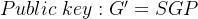
5.2 加密算法

信道内错误信息满足如下：

 

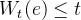
借助公钥，得到的密文如下：

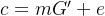
5.3解密算法

解密第一步，利用密文和概率P得到如下：

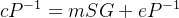
第二步利用快速解码算法，计算出mS。第三步即可恢复出明文m如下：

六.安全通信分析

借助以上极化过程，合法接收者Bob和窃听者Eve的信道会出现如下情况：

要实现安全通信，则需要利用对于Bob无噪，而对于Eve全噪的部分。以块的形式进行分析可得如下：

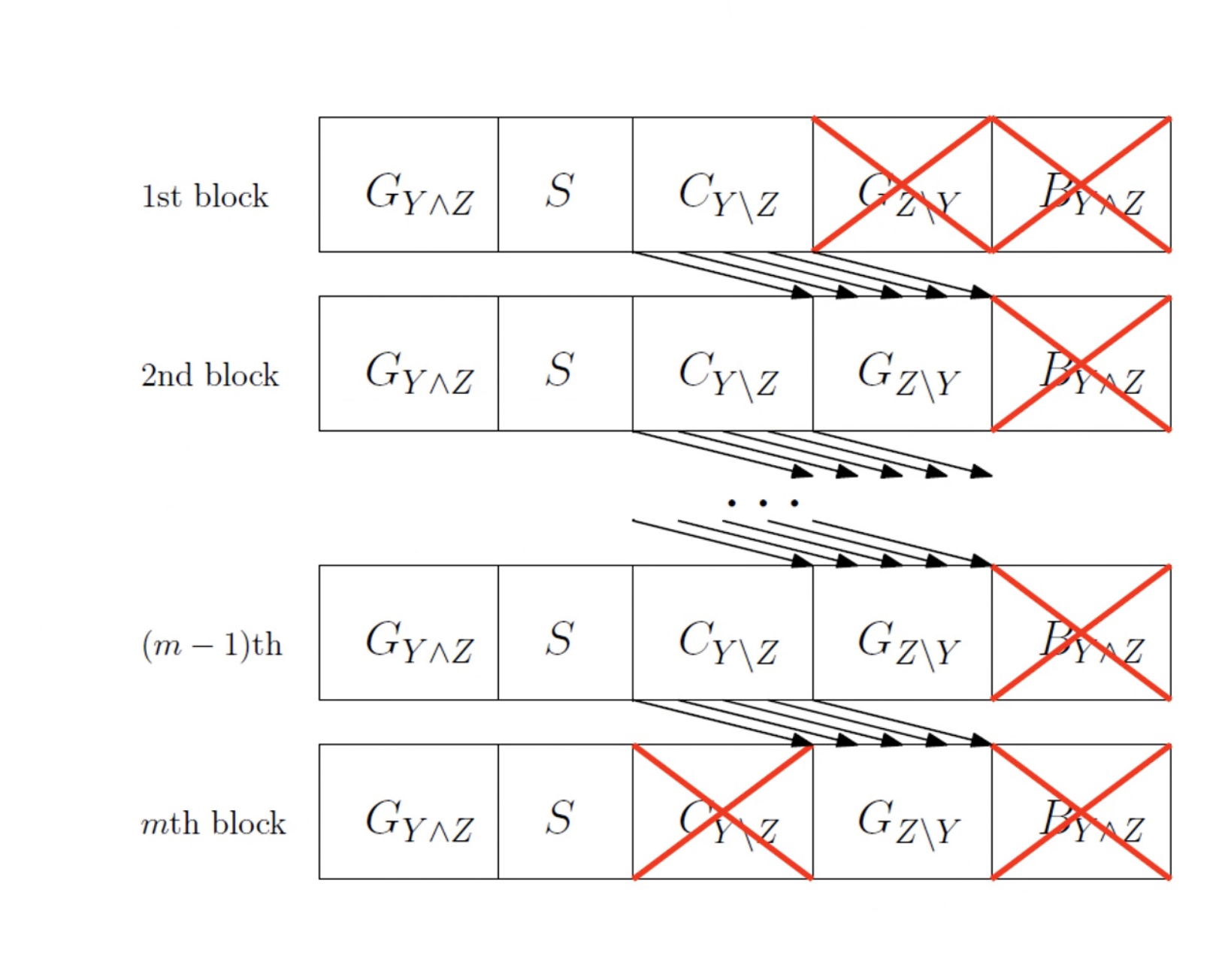
极化码主要可实现物理层的安全通信，包含弱安全和强安全，在此处可列举出一些重要的参考文献：

消息首先经过信源编码形成x，接着借助极化码形成c，经过信道传输到接收端形成y，接收端首先利用极化解码成x，在经过安全编码即可译码出消息m，将此处安全通信形成流程图如下：