【模拟】螺旋矩阵问题

题目描述：

给定一 m*n 的矩阵，请按照逆时针螺旋顺序，返回矩阵中所有元素。

示例：

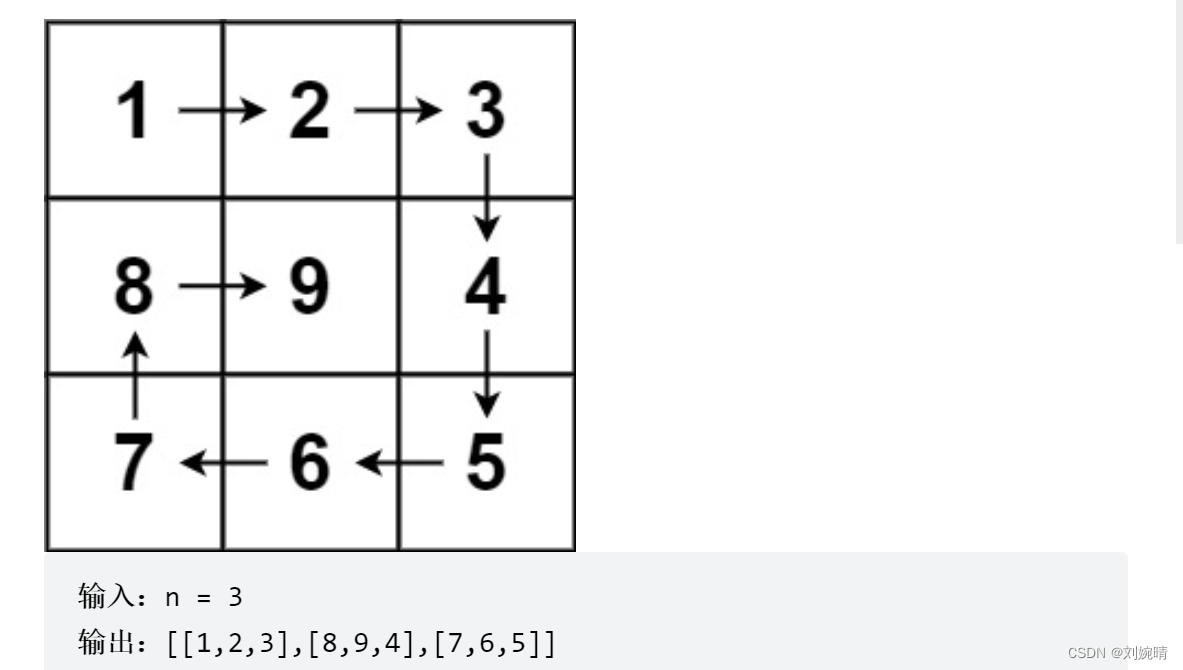
思路：

这是一道典型的模拟问题：
我们可以分析一下，遍历前进轨迹: 向右 - > 向下 -> 向左 -> 向上 -> 向右 …
于是，我们可以在循环中模拟这样的前进轨迹，记录 右，下，上左，四个边界，每次拐弯时更新边界值，再进行下一次拐弯，循环往复，直至结束。结束条件为 左边界加一大于右边界，或者上边界加一大于下边界。

图解：

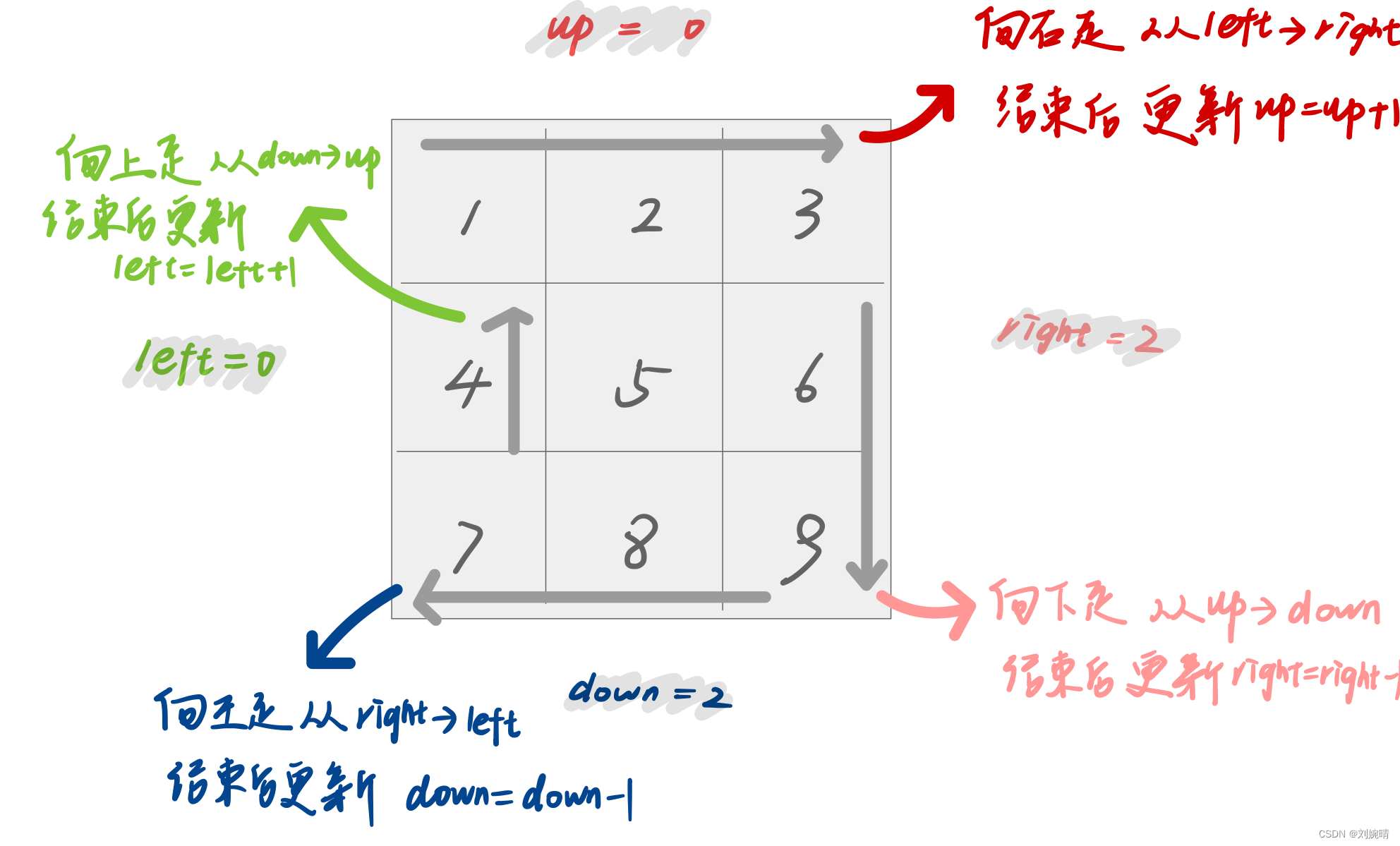
代码：

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> list = new ArrayList<Integer>();
        // 思路： 注意上下左右边界 —— 走格子法（一直走，一直走，直到走完了，出去）
        int left = 0;
        int right = matrix[0].length - 1;
        int up = 0;
        int down = matrix.length - 1;
        if(right==-1 || down==-1){
            return list;
        }
        while(true){
            // 向右走
            for(int i=left; i<=right; i++){
                list.add(matrix[up][i]);
            }
            // 判断是否结束
            if(up+1 > down){
                break;
            } else{
                up++; // 更新上边界
            }
            // 向下走
            for(int i=up; i<=down; i++){
                list.add(matrix[i][right]);
            }
            // 判断是否结束
            if(right - 1 < left){
                break;
            } else{
                right--; // 更新右边界
            }
            // 向左走
            for(int i=right; i>=left; i--){
                list.add(matrix[down][i]);
            }
            // 判断是否结束
            if(down-1 < up){
                break;
            } else{
                down--; // 更新下边界
            }
            // 向上走
            for(int i=down; i>=up; i--){
                list.add(matrix[i][left]);
            }
            // 判断是否结束
            if(left + 1 > right ){
                break;
            } else{
                left++; // 更新左边界
            }
        }
        return list;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

---

---

变式一：

题目描述：

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例：

代码:

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] ans = new int[n][n];
        int left = 0;
        int right = n - 1;
        int up = 0;
        int down = n - 1;
        int start = 1;
        while(true){
            // 向右
            for(int i=left; i<=right; i++){
                ans[up][i] = start;
                start++;
            }
            if(++ up > down){
                break;
            }
            
            // 向下
            for(int i=up; i<=down; i++){
                ans[i][right] = start;
                start++; 
            }
            if(-- right < left){
                break;
            }
            // 向左
            for(int i=right; i>=left; i--){
                ans[down][i] = start;
                start++;
            }
            if(-- down < up){
                break;
            }
            // 向上
            for(int i=down; i>=up; i--){
                ans[i][left] = start;
                start++;
            }
            if(++ left > right){
                break;
            }
        }
        return ans;
    }  
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46