史上最简SLAM零基础解读(8) - g2o(图优化)→示例代码讲解

本人讲解关于slam一系列文章汇总链接:史上最全slam从零开始
 
$文末正下方中心提供了本人联系方式，点击本人照片即可显示WX\to 官方认证$
 

一、前言

示例代码为 https://github.com/gaoxiang12/slambook2/blob/master/ch6/g2oCurveFitting.cpp

在g2o简介的博客中，讲解了运行该示例代码环境的搭建，同时对 g2o 进行了简单的讲解。然后又对 $顶点(Vertex)$ 与 $边(Edge)$ 进行详细分析，总的来说使用 g2o 进行优化,编程求解主要包含五个步骤，来看看代码编程的流程：

$(1)$ 顶点和边的类型定义；

$(2)$ 构建图优化实例，配置求解器；

$(3)$ 添加点和边，构建求解图；

$(4)$ 执行优化。

后续，会把源码拆解成这四个部分，分别进行讲解。在这之前，先说一下示例代码的目的。虽然前面的博客已经把代码运行了起来，但是并没有讲具体实现是的功能是什么。假设一条满足以下方程的曲线:
$$y=\exp \left(a{x}^2+bx+c\right)+w\text{\hspace{1em}(01)}$$其中 $a，b，c$ 为曲线的参数，$w$ 为高斯噪声，满足 $w\sim \left(0,{\sigma }^2\right)$。我们故意选择了这样一个非线性模型，使问题不至于太简单。现在，假设我们有 $N$ 个关于 $x,y$ 的观测数据点，想根据这些数据点求出曲线的参数。那么，可以求解下面的最小二乘问题以估计曲线参数:$$\underset{a,b,c}{\min }\frac{1}{2}\sum _{i=1}^N{\Vert y_i-\exp \left(a{x}_i^2+b{x}_i+c\right)\Vert }^2\text{\hspace{1em}(02)}$$请注意，在这个问题中，待估计的变量是 $a，b，c$；而不是 $x$。我们的程序里先根据模型生成 $x，y$ 的真值，然后在真值中添加高斯分布的噪声。使用 g2o 从带噪声的数据拟合参数模型。定义误差为：$$e_i=y_i-\exp \left(a{x}_i^2+b{x}_i+c\right)\text{\hspace{1em}(03)}$$那么，可以求出每个误差项对于状态变量的导数:
∂ e i ∂ a = − x i 2 exp ⁡ ( a x i 2 + b x i + c ) ∂ e i ∂ b = − x i exp ⁡ ( a x i 2 + b x i + c ) ∂ e i ∂ c = − exp ⁡ ( a x i 2 + b x i + c ) (04) \color{green} \tag{04}

∂a∂ei​​=−xi2​exp(axi2​+bxi​+c)∂b∂ei​​=−xi​exp(axi2​+bxi​+c)∂c∂ei​​=−exp(axi2​+bxi​+c)​(04)
下面就从每个步骤来分析吧，这里就不在粘贴整体的源码了，前面链接已经给出。如果对Jacobian matrix(雅可比矩阵)不太熟悉的朋友，建议先阅读下面这篇博客。

$推荐$：史上最简SLAM零基础解读(7) - Jacobian matrix(雅可比矩阵) → 理论分析与应用详解
 

二、数据模拟

首先需要去模拟一些数据，假设(01)式中真实的 a b c _ r = { a = 1.0 ， b = 2.0 ， b = 1.0 } abc\_r=\{a=1.0，b=2.0，b=1.0\} abc_r={a=1.0，b=2.0，b=1.0}，需要优化的初始值设定为 a b c _ e = { a = 2.0 ， b = − 1.0 ， c = 5.0 } abc\_e=\{a = 2.0，b = -1.0，c= 5.0\} abc_e={a=2.0，b=−1.0，c=5.0}。 也就是说，通过优化之后，使得 $abc\_e$ 接近于 $abc\_r$。现在利用 $abc\_r$ 随机生成 $N=100$ 组数据(同时添加了噪声)。代码如下：

  double ar = 1.0, br = 2.0, cr = 1.0;         // 真实参数值
  double ae = 2.0, be = -1.0, ce = 5.0;        // 估计参数值
  int N = 100;                                 // 数据点
  double w_sigma = 1.0;                        // 噪声Sigma值
  double inv_sigma = 1.0 / w_sigma;
  cv::RNG rng;                                 // OpenCV随机数产生器

  vector<double> x_data, y_data;      // 数据
  for (int i = 0; i < N; i++) {
    double x = i / 100.0;
    x_data.push_back(x);
    y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
  }
1
2
3
4
5
6
7
8
9
10
11
12
13

 

三、点和边的类型定义

1、顶点类型的定义

// 曲线模型的顶点，模板参数：优化变量维度和数据类型
class CurveFittingVertex : public g2o::BaseVertex<3, Eigen::Vector3d> {
public:
	//类成员变量如果是固定大小对象需要加上 EIGEN_MAKE_ALIGNED_OPERATOR_NEW
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW

  // 重置；override 重载　
  virtual void setToOriginImpl() override {
    _estimate << 0, 0, 0;
  }

  // 更新
  virtual void oplusImpl(const double *update) override {
    _estimate += Eigen::Vector3d(update);
  }

  // 存盘和读盘：留空
  virtual bool read(istream &in) {}

  virtual bool write(ostream &out) const {}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

顶点类成员继承继承自BaseVertex，模板成员参数分别是 3，Eigen::Vector3d。其表示的意思是待优化变量类型为 Eigen::Vector3d，维度是3。另外顶点类包含四个重要的成员函数需要重载:

$(1)$ setToOriginImp()用于重置优化变量值。(改)
$(2)$ oplusImpl()用于对优化变量进行更新调整，是优化变量向真实值靠近(改)
$(3)$ read和write分别是读盘、存盘函数，一般情况下不需要进行读/写操作的话，仅仅声明一下就可以.

2、边类型的定义

// 误差模型 模板参数：观测值维度，类型，连接顶点类型
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
    //类成员变量如果是固定大小对象需要加上 EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    //构造函数初始化
    CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}
    // 计算曲线模型误差
    virtual void computeError() override
    {
        //顶点获取
        const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
        //优化变量获取
        const Eigen::Vector3d abc = v->estimate();
        //惨差计算
        _error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
    }
    // 计算雅可比矩阵
    virtual void linearizeOplus() override
    {
        //顶点获取
        const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
        //优化变量获取
        const Eigen::Vector3d abc = v->estimate();
        //数值求导
        double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
        _jacobianOplusXi[0] = -_x * _x * y;
        _jacobianOplusXi[1] = -_x * y;
        _jacobianOplusXi[2] = -y;
    }
    //读写，暂时不用，留空
    virtual bool read(istream &in) {}
    virtual bool write(ostream &out) const {}
private:
    double _x;  // x 值， y 值为 _measurement
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

边类成员继承继承自BaseUnaryedge(不同类型的边有不同的基类，这里是一元边基类)，模板成员参数分别是：1，double, CurveFittingVertex。这里的1表示观测变量维度，double 表示观测变量数据类型。CurveFittingVertex 表示前面定义的顶点类型。边类包含四个重要的成员函数需要重载:

$(1)$ virtual void computeError(); 计算惨差，通过成员变量_vertices[0]和顶点编号０获取０号顶点变量；之后通过estimate()成员函数获取最近的优化变量；最后通过 _measurement中存储的观测变量与优化变量做参差计算并传给_error(0, 0)。(改)

$(2)$ virtual void linearizeOplus(); 同样获取顶点并获取待优化的变量，最后通过数值求导获取雅克比梯度，注意这里需要添加负号，利用负梯度方向迭代。(改)

$(3)$ read 、write留空。
 

四、构建图优化实例，配置求解器

 // 第二部分；配置优化器，构建图优化
    // 定义重载求解变量块，每个误差项优化变量维度为3，误差值维度为1
    typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType;
    // 定义线性求解器类型
    typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;
    //创建高斯牛顿求解器
    auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
    // 图模型
    //创建稀疏优化器
    g2o::SparseOptimizer optimizer;
    // 设置求解器
    optimizer.setAlgorithm(solver);
    // 打开调试输出
    optimizer.setVerbose(true);
1
2
3
4
5
6
7
8
9
10
11
12
13
14

$(1)$ 定义变量块BlockSolverType，模板参数分别表示
①优化变量维度(３）
②误差变量维度(１)

$(2)$ 定义线性求解器LinearSolverType。

$(3)$ 选取求解方法。

$(4)$ 创建并配置稀疏优化器。
 

五、添加点和边

//　第三部分；添加点和边
    // 实例化顶点，往图中增加顶点
    CurveFittingVertex *v = new CurveFittingVertex();
    //配置初始估计值
    v->setEstimate(Eigen::Vector3d(aest, best, cest));
    //设置图表中节点的id确保更改id后图表保持一致
    v->setId(0);
    //添加设置完成的顶点
    optimizer.addVertex(v);

    // 往图中增加边
    for (int i = 0; i < PointNum; i++)
    {
        //实例化边，并传入标点值
        CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
        //设置图表中边的id确保更改id后图表保持一致
        edge->setId(i);
        // 设置连接的顶点，１、顶点编号２、顶点实例化
        edge->setVertex(0, v);
        // 传入观测到的数值
        edge->setMeasurement(y_data[i]);
        // 设置信息矩阵：协方差矩阵之逆
        edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma));
        //将设置完成的边加入
        optimizer.addEdge(edge);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

$(1)$ 实例化一个点ｖ；传入优化变量的初始估计值；给顶点配置编号；将顶点添加至图中。
$(2)$ 实例化边edge；给边配置编号；配置链接的顶点信息（顶点的编号，顶点的实例化）；传入观测值；配置信息矩阵；将边添加至图。

六、添加点和边

执行优化与输出：

  // 执行优化
  cout << "start optimization" << endl;
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  optimizer.initializeOptimization();  
  optimizer.optimize(10);   //优化次数
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "solve time cost = " << time_used.count() << " seconds. " << endl;

  // 输出优化值
  Eigen::Vector3d abc_estimate = v->estimate();
  cout << "estimated model: " << abc_estimate.transpose() << endl;
1
2
3
4
5
6
7
8
9
10
11
12

答应结果如下

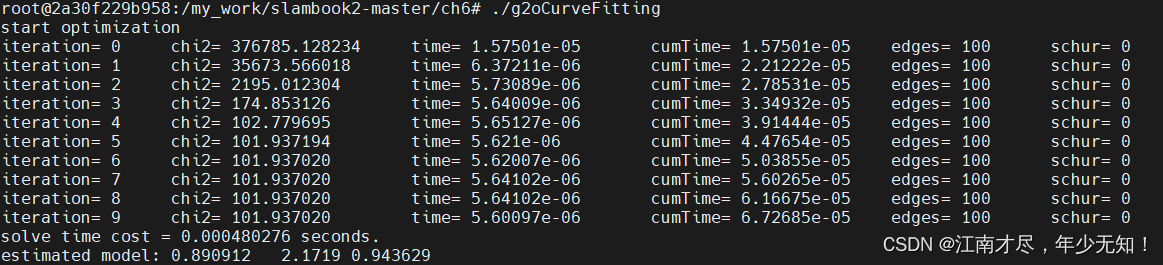
最终预测的结果为 $a=0.89012，b=2.1719，c=0.943629$。可以看到其与真实值 a b c _ r = { a = 1.0 ， b = 2.0 ， b = 1.0 } abc\_r=\{a=1.0，b=2.0，b=1.0\} abc_r={a=1.0，b=2.0，b=1.0} 还是存在一定差距，但是已经非常接近了。其主要原因是因为生成的数据带噪声的，宁外我们只优化迭代了10次。

 

七、结语

通过前面两篇博客，可以说是对 g2o(图优化) 有了简单的了解，g2o(图优化) 在 slam 中有着举足轻重的地位。如果要去追根究底底层的源码，说实话，难度还是比较大的。但是如果只是当作一个工具包来使用，还是比较简单的。主要的难点在于顶点和边的创建。不过没有关系，等大家看别人的源码看得比较多了，就熟悉 g2o(图优化) 具体应该怎么去使用与设计了。