数据结构与算法之非递归遍历二叉树

非递归遍历二叉树

前序遍历

逻辑：

1. 访问结点 P，并将结点 P 入栈;
2. 判断结点 P 的左孩子是否为空，若为空，则取栈顶结点并进行出栈操作，并将栈顶结点的右孩子置为当前的结点 P，循环至1; 若不为空，则将 P 的左孩子置为当前的结点 P;
3. 直到 P 为 NULL 并且栈为空，则遍历结束。

代码实现

/**  
 * 非递归前序遍历二叉树  
 * 1. 访问结点 P，并将结点 P 入栈;  
 * 2. 判断结点 P 的左孩子是否为空，若为空，则取栈顶结点并进行出栈操作，并将栈顶结点的右孩子置为当前的结点 P，循环至1;  
 * 若不为空，则将 P 的左孩子置为当前的结点 P;  
 * 3. 直到 P 为 NULL 并且栈为空，则遍历结束。  
 *  
 * @param p 根节点  
 */  
void preOrderByStack(TreeNode p) {  
    Stack stack = new Stack<>();  
    stack.push(p);  
    while (p != null || !stack.empty()) {  
        while (p != null) {  
            System.out.println(p.val);  
            stack.push(p);  
            p = p.left;  
        }  
        if (!stack.empty()) {  
            p = stack.pop();  
            p = p.right;  
        }  
    }  
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

中序遍历

逻辑：

对于任一结点 P，

1. 若其左孩子不为空，则将 P 入栈并将 P 的左孩子置为当前的 P，然后对当前结点 P 再进行相同的处理；
2. 若其左孩子为空，则取栈顶元素并进行出栈操作，访问该栈顶结点，然后将当前的 P 置为栈顶结点的右孩子；
3. 直到 P 为 NULL 并且栈为空则遍历结束

代码实现

/**  
 * 非递归前序遍历二叉树  
 * 1. 若其左孩子不为空，则将 P 入栈并将 P 的左孩子置为当前的 P，然后对当前结点 P 再进行相同的处理；  
 * 2. 若其左孩子为空，则取栈顶元素并进行出栈操作，访问该栈顶结点，然后将当前的 P 置为栈顶结点的右孩子；  
 * 3. 直到 P 为 NULL 并且栈为空则遍历结束  
 *  
 * @param p 根节点  
 */  
void midOrderByStack(TreeNode p) {  
    Stack stack = new Stack<>();  
    stack.push(p);  
    while (p != null && !stack.empty()) {  
        while (p != null) {  
            stack.push(p);  
            p = p.left;  
        }  
        if (!stack.empty()) {  
            p = stack.pop();  
            System.out.println(p.val);  
            p = p.right;  
        }  
    }  
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

后序遍历(复杂一点)

后序遍历的非递归实现是三种遍历方式中最难的一种。因为在后序遍历中，要保证左孩子和右孩子都已被访问并且左孩子在右孩子前访问才能访问根结点，这就为流程的控制带来了难题。下面介绍两种思路。可以观察下图头脑风暴一下：

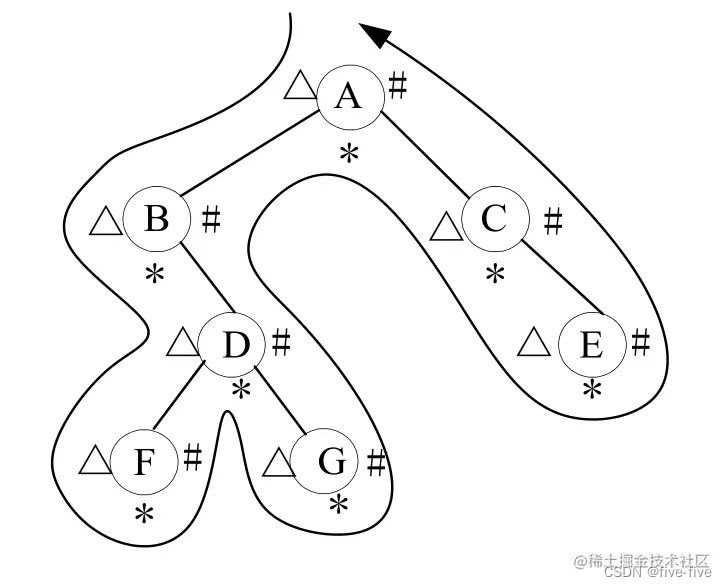
方法一

第一种思路：对于任一结点 P，将其入栈，然后沿其左子树一直往下搜索，直到搜索到没有左孩子的结点，此时该结点出现在栈顶，但是此时不能将其出栈并访问，因此其右孩子还未被访问。所以接下来按照相同的规则对其右子树进行相同的处理，当访问完其右孩子时，该结点又出现在栈顶，此时可以将其出栈并访问。这样就保证了正确的访问顺序。可以看出，在这个过程中，每个结点都两次出现在栈顶，只有在第二次出现在栈顶时，才能访问它。因此需要多设置一个变量标识该结点是否是第一次出现在栈顶。

这种方式需要重新在申请一个结构体，这里推荐方法二

方法二

逻辑：

建议观看视频：二叉树遍历-后序(非递归)【图解+代码】_哔哩哔哩_bilibili

---

1. 首先设置一个变量，用来记录访问过的右结点这里以pre为例，然后遍历所有左节点，并压入栈中；
2. 判断栈顶元素是否有右结点(此时还未进行弹栈操作)
   1. 有右节点并且已经访问过或者是无右节点，则直接输出，并且将pre置为当前结点cur，在把当前结点p置为空，以防下次循环重复遍历左子树，最后将栈顶元素弹出
   2. 有右节点但是未被访问过，将当前结点置为右节点，并进行右节点树的遍历，即将当前结点置为cur.right并重复第一步

代码实现

/**  
 * 非递归后序遍历二叉树  
 *  
 * @param p 根节点  
 */  
void rearOrderByStack(TreeNode p) {  
    Stack stack = new Stack<>();  
    stack.push(p);  
    TreeNode pre = null;  
    while (p != null || !stack.empty()) {  
        while (p != null) {  
            stack.push(p);  
            p = p.left;  
        }  
        if (!stack.empty()) {  
            p = stack.peek();  
        }  
        assert p != null;  
        //栈顶有右子树且未被访问过  
        if (p.right != null && p.right != pre) {  
            p = p.right;  
        } else {  
            //访问当前结点  
            System.out.println(p.val);  
            pre = p;  
            //此时p是栈顶元素，直接将p置空，下次循环直接就是获取栈顶元素，避免重复访问左子树  
            p = null;  
            stack.pop();  
        }  
    }  
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

‍