CMSC5707-高级人工智能之音频信号预处理操作

这一章主要介绍了时域和频域的处理、傅立叶变换以及时频图，集中在相关概念的理解上。

本文参考：

语音信号处理之（四）梅尔频率倒谱系数（MFCC）

音帧处理Frame blocking and Windowing

这有点像小时候一帧一帧的手翻画，在处理音频信号的时候也习惯将信号处理成固定帧大小，需要建立这种意识意识，后面的傅立叶变换、线性预测编码都是基于音帧来处理的。其中Frame Size就是指一帧的大小，通常是指一个窗口中有的样本个数或者也指一个窗口覆盖的时间，同样可以结合取样频率计算出一个窗口内的样本个数。Adjacent frames seperated by m samples，这指的是两个窗口间相差的距离，也叫做hop_size，non-overlap samples。

习题1:

Hamming window约束

傅立叶变换能够将时域转变为频域，但是在转变前，音帧的开头和结尾不具有连续性，突然地改变signal level会产生的巨大能量，在之后傅立叶变换的频域图像中产生噪声。

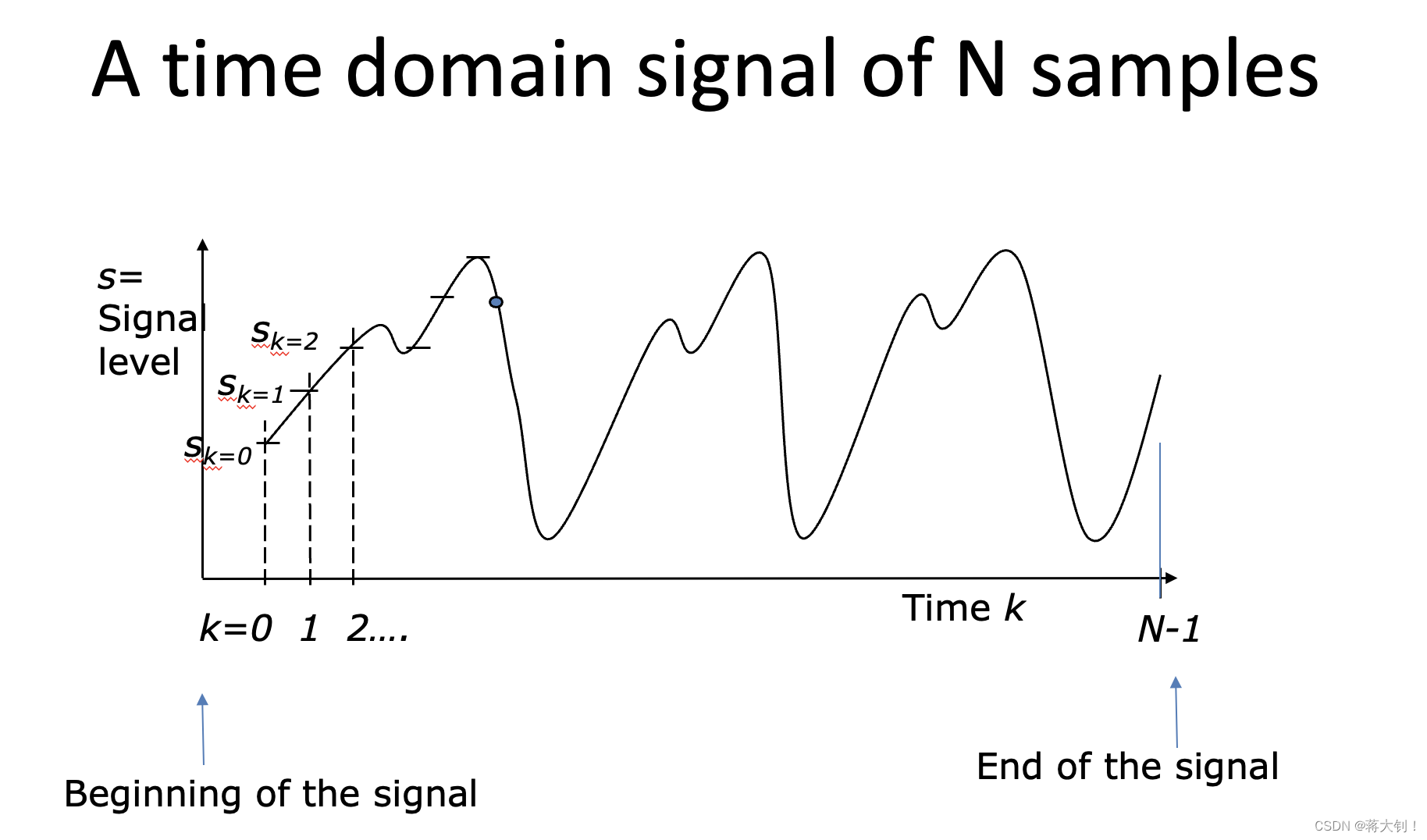
Hamming window相当于就是一个系数，如图中的W(k)，针对原时域图中的每个点的Signal level，我都用这样一个系数相乘进行约束，最终产生的效果如下所示，有效地平滑了开始和结束时刻的波动：

傅立叶变换（Fourier Transform）与频谱图（Spectrum）

感性理解

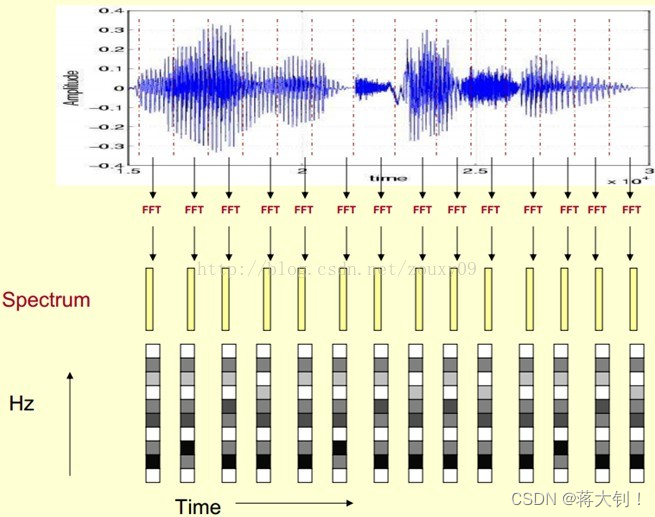
在这里，一段语音对应着很多帧，每帧语音都通过一次傅立叶变换（FFT）转换成频谱，频谱可以表示一帧语音能量和频率的关系。

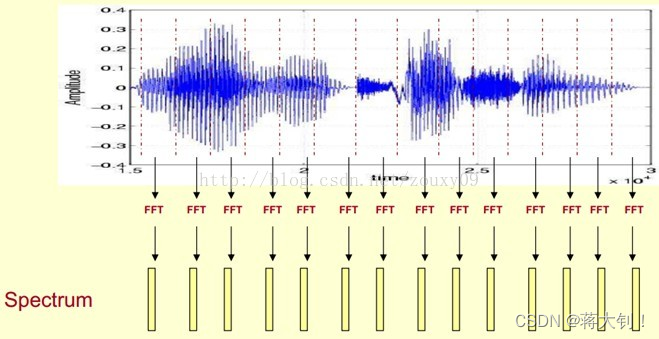
傅立叶变换通过公式计算，能够将原先时域的信息转换到频域上来，原先横坐标为时间，现在的横坐标变为频率。下面就是傅立叶变换得到的频谱图，对应上面每段黄色的矩形。

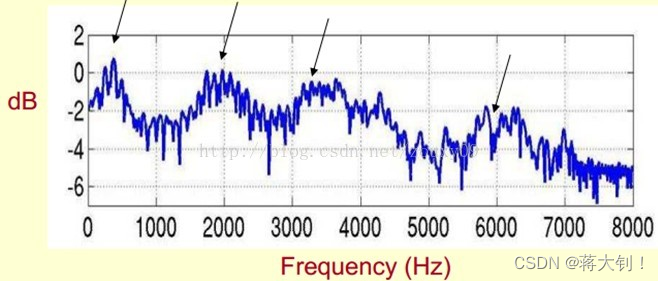
峰值就表示语音的主要频率成分，我们把这些峰值称为共振峰（formants），而共振峰就是携带了声音的辨识属性（就是个人身份证一样）。所以它特别重要。用它就可以识别不同的声音。我们将共振峰包括它们的转变过程绘制成一条平滑的曲线，称之为频谱的包络（Spectral Envelope）。

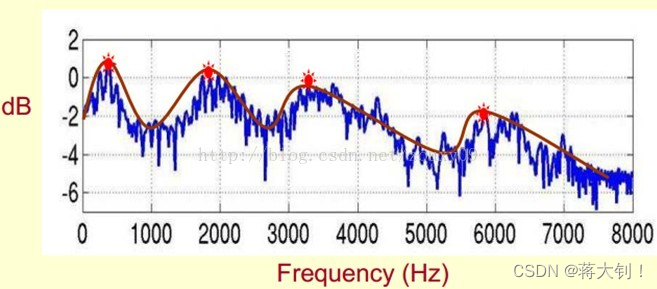
理性计算

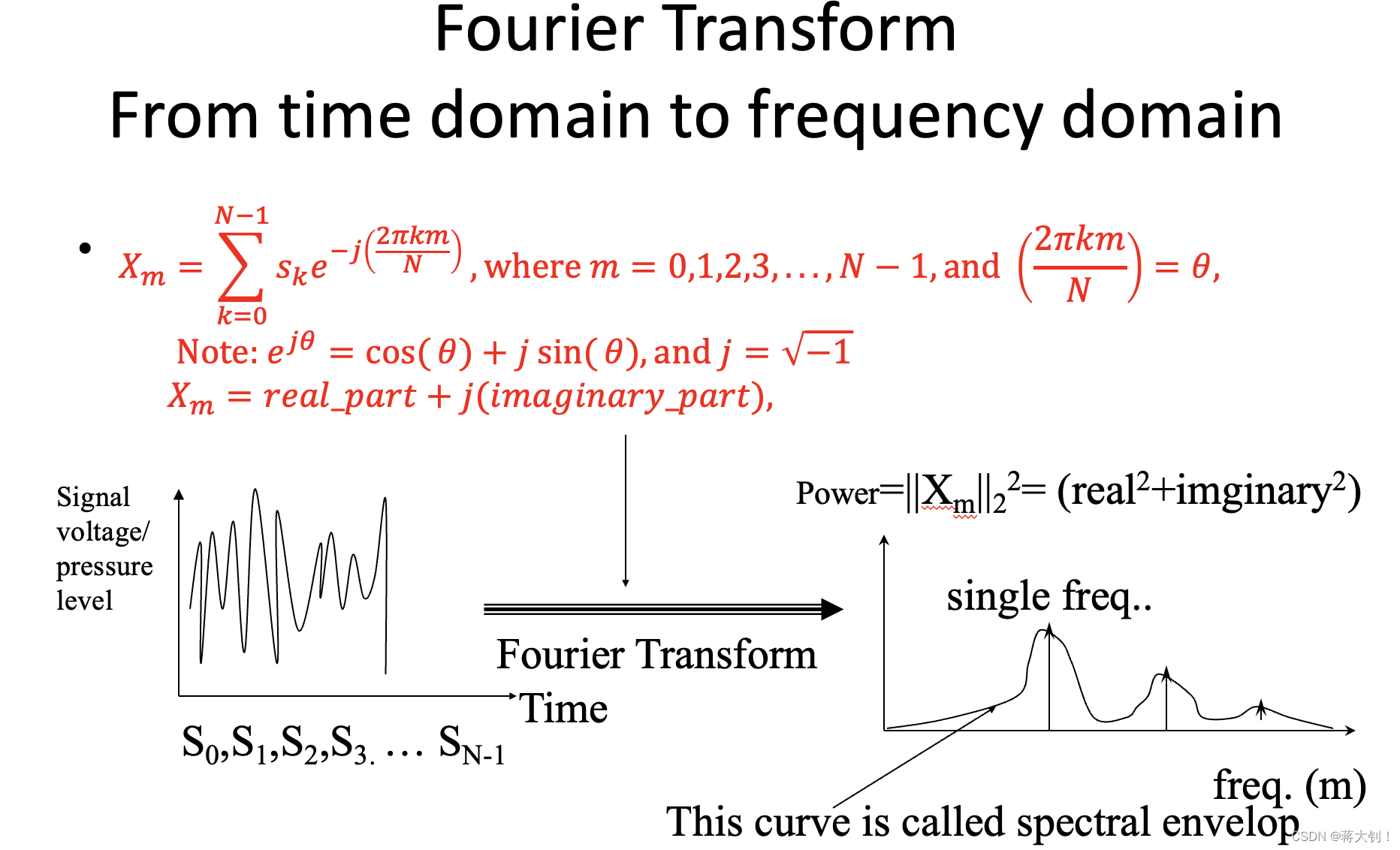
傅立叶变换聚焦于一个音帧，如果一个音帧窗口大小为N，就能输出N（有些资料中为N/2）个关于频率的复数Xm（m=0,1,…N-1（或者N/2-1）），Xm分为实部real_part和虚部imaginary_part，每个Xm都对应着一个累加求和的过程，即$X_m={\sum }_{k=0}^{N-1}{s}_k{e}^{-j\left(\frac{2\pi km}{N}\right)}$，通过$e^{-j\theta }=\cos (\theta )-j\sin (\theta )$能够将这个公式中所有的$e^{-j\theta }$拆开求和合并，其中实部对应着$\cos (\theta )$，虚部对应着$-\sin (\theta )$。整体在对一个音帧的每个复数Xm进行计算的时候，是双层循环，伪代码如下：

一个用真实数据带入的例子如下，其中只是列出来了每个复数求和累加的过程，还没有把对应的实部real_part和虚部imaginary_part分别相加化简：

我又去额外了解了一下，这个转换后的频域中的Xk和转换前的频率有什么关系。假如采样频率Sampling Frequency为25600Hz，我们连续采样 256 个数据来做离散傅立叶变换，则变换到频域图后，我们能看到的最小频率间隔（即Xk的间隔）为25600/256=100Hz，在频域图中就是从0开始每隔100Hz绘制一个点。如果我们采样的声音的频率Sound Frequency为200Hz，我们就能在频域图中看到其对应的能量。

时频图Spectrogram

时频图Spectrogram相当于就是将三个维度的信息全部在一张图像上展现出来，包括时间、频率以及随频率变化的能量，如下图所示，横坐标是时间，纵坐标是频率，颜色代表能量，颜色越白能量越大。

垂直地看，每一个窗口都是一段音帧通过傅立叶变换FT产生的能量随频率变化的图像。在每段音帧傅立叶变换的基础上增加时间这个维度，这样就可以显示一段语音而不是一帧语音的频谱，而且可以直观的看到静态和动态的信息。

时频图展示出来的重点信息随窗口大小的变化也不同，窗口越大，频率分辨率越好，窗口越小，时间分辨率越好。