Leetcode 222. 完全二叉树的节点个数

1.题目描述

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ $2^h$ 个节点。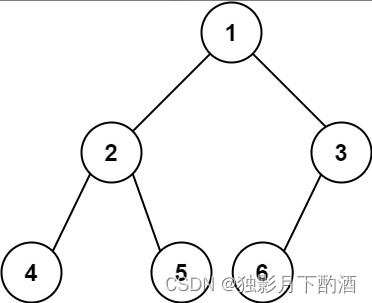

输入：root = [1,2,3,4,5,6]
输出：6

输入：root = []
输出：0

输入：root = [1]
输出：1

提示：

• 树中节点的数目范围是$[0,5\ast 10^4]$
• $0<=Node.val<=5\ast 10^4$
• 题目数据保证输入的树是 完全二叉树

2.思路分析

2.1 递归法

1.确定递归函数的参数以及返回值

• 参数:根节点
• 返回值:以该节点为根节点二叉树的节点数量

def countNodes(self, root: Optional[TreeNode]) -> int:
1

2.确定终止条件

如果节点为空, 返回0, 表示节点数为0。

if not root:
    return 0
1
2

3.确定单层递归的逻辑

先求它的左子树的节点数量，再求它的右子树的节点数量, 最后取总和在加1即可

self.countNodes(root.left) + self.countNodes(root.right) + 1
1

2.2 迭代法

使用队列模拟栈操作, 遍历整棵树。

2.3 据完全二叉树的性质简化遍历次数

完全二叉树只有两种情况:

• 情况一：满二叉树，节点数:$2^{(}树的深度)-1$(根节点深度=1)

• 情况二：最后一层叶子节点没有满。 分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。
  

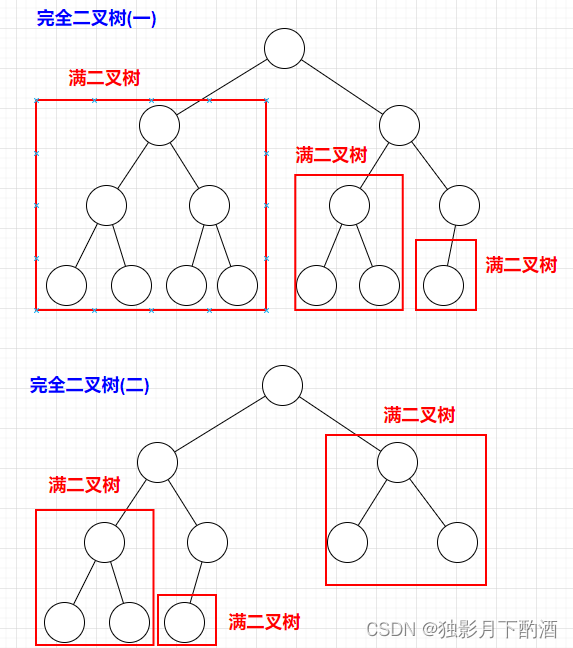
关键在于如果去判断一个左子树或者右子树是不是满二叉树呢？

在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树 。

3.代码实现

3.1 递归法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
         # 递归法
         if not root:
             return 0
         else:
             return self.countNodes(root.left) + self.countNodes(root.right) + 1
1
2
3
4
5
6
7
8
9
10
11
12
13

复杂度分析:

• 时间复杂度：O(n)。
• 空间复杂度：O(log n)，算上了递归系统栈占用的空间。

3.2 迭代法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        # 迭代法
        result = 0
        if not root:
            return result

        from collections import deque
        que = deque([root])

        while que:
            size = len(que)
            for _ in range(size):
                cur = que.popleft()
                result += 1

                if cur.left:
                    que.append(cur.left)

                if cur.right:
                    que.append(cur.right)
        return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

复杂度分析:

• 时间复杂度：O(n)。
• 空间复杂度：O(n)。

3.3 据完全二叉树的性质简化遍历次数

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        # 利用完全二叉树的特性
        if not root:
            return 0
        left, right = root.left, root.right
        leftHeight, rightHeight = 0, 0
        while left: #求左子树深度
            left = left.left
            leftHeight += 1
        while right: #求右子树深度
            right = right.right
            rightHeight += 1
        if leftHeight == rightHeight:#判断子树是不是完满二叉树
            return (2 << leftHeight) - 1 #注意(2<<1) 相当于2^2，所以leftDepth初始为0
        return 1 + self.countNodes(root.left) + self.countNodes(root.right)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

复杂度分析:

• 时间复杂度：O(logn * logn)。
• 空间复杂度：O(logn)。