【机器学习】逻辑回归logit与softmax

模型训练导航：
【机器学习】模型训练：scikitLearn线性模型的公式法与三种梯度下降法求解
【机器学习】欠拟合及过拟合与学习曲线、误差来源
【机器学习】scikitLearn正则化l1,l2,提前停止

逻辑回归（Logistic回归，也称为Logit回归）被广泛用于估算一个实例属于某个特定类别的概率。
与线性回归模型一样，逻辑回归模型也是计算输入特征的加权和（加上偏置项），但是不同于线性回归模型直接输出结果，它输出的是结果的数理逻辑值。
数理逻辑函数sigmoid:输出的值是0到1的数理逻辑值

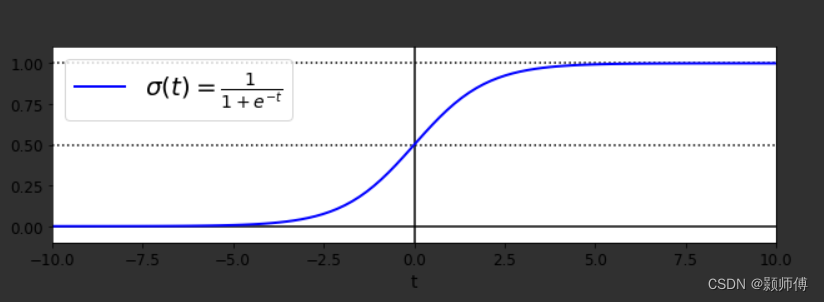
当t＜0时，σ（t）＜0.5；当t≥0时，σ（t）≥0.5。所以如果是正类，逻辑回归模型预测结果是1，如果是负类，则预测为0。
即

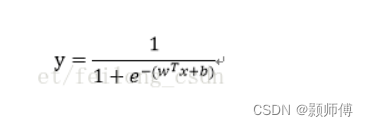
变形为：

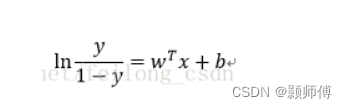
左侧是正例与负例概率比取对数，名为logit函数。

训练逻辑回归的成本函数为：

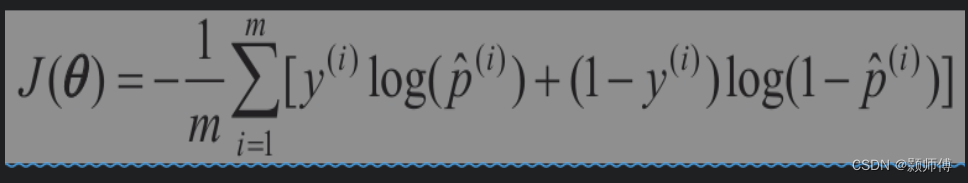
我们假定概率值0代表负类，概率值1代表正类。
上述函数保证了如果正类的概率值被判定接近0，及负类的概率接近1，成本函数的值都会非常高。

这是个凸函数，所以通过梯度下降（或是其他任意优化算法）保证能够找出全局最小值。

这其实是交叉熵在2分类中特殊的表示形式，其一般形式为：

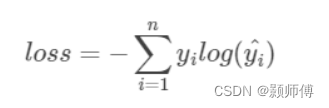
交叉熵的值越小，y和y预测这两个分布间越接近。
对应代码：

from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression(solver="lbfgs", random_state=42)
log_reg.fit(X, y)
1
2
3

Softmax回归：逻辑回归的推广
逻辑回归模型经过推广，可以直接支持多个类别，而不需要训练并组合多个二元分类器。
原理很简单：给定一个实例x，Softmax回归模型首先计算出每个类k的分数sk（x），然后对这些分数应用softmax函数（也叫归一化指数），估算出每个类的概率。
Softmax回归分类器预测具有最高估计概率的类（简单来说就是得分最高的类）
Softmax回归分类器一次只能预测一个类（即它是多类，而不是多输出），因此它只能与互斥的类（例如不同类型的植物）一起使用。

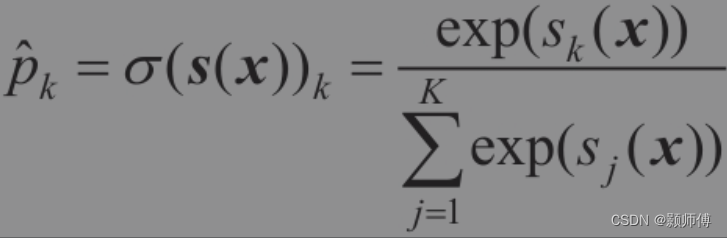
训练时同样采用交叉熵函数作为成本函数。（交叉熵与相对熵仅差一个常数，一般均使用交叉熵）
当用两个以上的类训练时，Scikit-Learn的LogisticRegressio默认选择使用的是一对多的训练方式，不过将超参数multi_class设置为"multinomial"，可以将其切换成Softmax回归。

X = iris["data"][:, (2, 3)]  # petal length, petal width
y = iris["target"]

softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=42)
softmax_reg.fit(X, y)
1
2
3
4
5

C值越高，对模型正则化要求越少。

softmax_reg.predict_proba([[5, 2]])
array([[6.38014896e-07, 5.74929995e-02, 9.42506362e-01]])
1
2

得出结果为3者的概率值。