开发者说论文｜人工智能为设备磨损“把脉”：依托飞桨开展的铁谱图像智能故障诊断研究...

在人工智能领域，深度学习平台的重要性毋庸置疑。飞桨是百度自研的深度学习平台，飞桨社区的开发者基于飞桨平台积极的将自己的智慧应用到前沿技术的研究中，为人工智能长期研发目标贡献自己的力量。为此，飞桨开发者说专栏推出论文专题，给予飞桨社区开发者一个平台，介绍学术研究的最新发展动向，分享在学术研究方面的经验。

本期文章将为大家分享飞桨开发者技术专家（PPDE）谢飞发表于ScienceDirect的文章《Research on controllable deep learning of multi-channel image coding technology in Ferrographic Image fault classification》

谢飞

中国财产再保险有限责任公司创新实验室高级承保师，上海市青年金才，百度飞桨开发者技术专家（PPDE），百度AICA项目四期班学员

在AI快车道等活动担任讲师，分享《新能源汽车火灾隐患检测》等内容，依托飞桨发表SCI机械类顶级期刊《Tribology International》论文《Research on controllable deep learning of multi-channel image coding technology in Ferrographic Image fault classification》。

机械设备的智能诊断是一种收集、处理和分析机械运转状态信息的技术，运用该类技术辅助设备维护和保养就是要基于相关信息对设备的状况进行诊断。该技术目前主要应用领域包括精密复杂的机械设备如飞机或船舶发动机、运行工况恶劣的大型机械如大型液压机及海上钻井平台设备等。

分析铁谱技术是一门对润滑系统中的磨损颗粒进行提取、观察，通过其数量、大小、形状和纹理等方面判断摩擦副润滑状况、磨损机理及磨损剧烈程度的技术。与其他故障诊断技术相比，具有前瞻性强、磨粒检测范围大、直接反映主要磨损机理等优点。然而，如图一所示，磨损颗粒的形貌特征较为复杂，形状上有片状、块状、层状、卷曲等类别，表面纹理有光滑、裂纹、坑洞、划痕等类别，颜色不一，尺寸各异，小颗粒由于磁化现象聚集在一起成为链状，互相遮挡重叠，自动分析的实现难度较大。

图1 铁谱图像

铁谱图像是需要进行专业提取和显微拍摄的图像，其制备过程需要利用摩擦磨损试验机、分析铁谱仪、光学显微镜等设备，制备成本高，图像数量少，因此，要开展相关智能识图研究就必须利用迁移学习技术。相较于通用计算机视觉领域，铁谱图像的智能识别是否可以利用通用视觉领域的预训练模型是研究人员面临的第一个问题。笔者评估两个域的差异程度，其依托于：

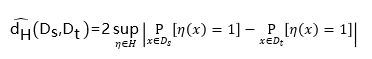
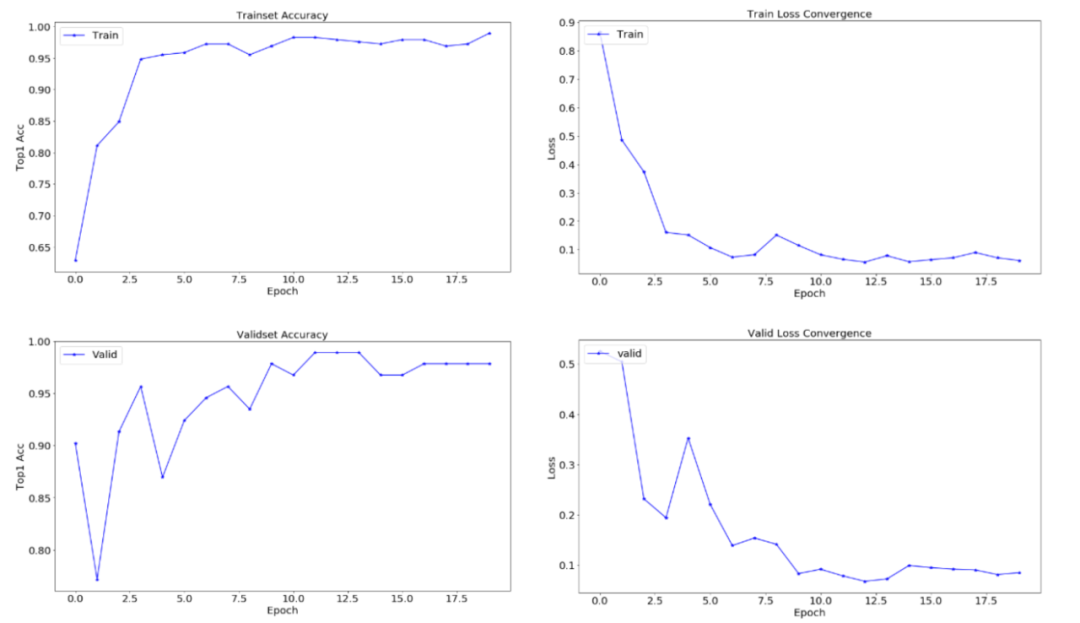
图2 基于ImageNet通用预训练模型的迁移学习结果

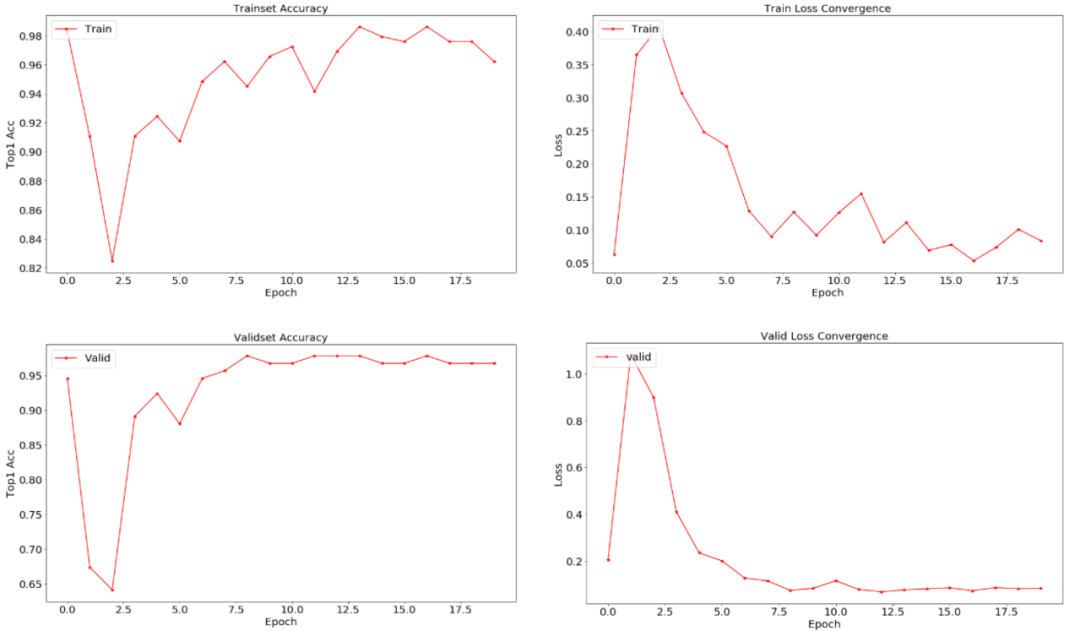
图3 基于铁谱图像故障诊断预训练模型的迁移学习结果

依托于飞桨框架，笔者完成了相关领域的测试并发现，对于铁谱图像故障诊断这个图像分类的下游任务，通过上述两组实验可以得到以下结论，即虽然依托ImageNet的通用预训练模型不完全适用于铁谱图像分类任务，且ImageNet训练数据与铁谱图像数据不完全服从同一分布，但是，依托ImageNet的通用预训练模型具有更好的模型自洽性（自适应性）、稳定性、泛化性和鲁棒性。因此依托ImageNet的通用预训练模型对铁谱图像进行微调的方法是有效且高精度的人工智能方法。

在此基础上，笔者搭建了基于CNN和ViT的铁谱图像智能诊断模型。PaddleViT 是一个基于最新深度学习技术的视觉模型和工具集合，提供了基于视觉Transformers技术、视觉注意力机制和MLP技术的前沿深度学习算法和预训练模型。

但是，直接将通用的视觉ViT模型应用到铁谱图像识别领域，其结果略逊于CNN卷积模型。笔者认为铁谱图像的识别与通用领域图像识别存在一些差别。这些差别可能源自于图像太少导致的过拟合，也可能源自于模型自主学到的某些特殊特征。但是，如何在现有小样本和图像背景下进行特定特征的识别并最终实现故障诊断，是相关研究者的重要研究方向。

为了解决上述问题，笔者期望故障诊断模型能够更加聚焦于铁谱的关键信息，这些信息包括磨粒的表面状况、边缘、形状和颜色等等，而忽略背景和无关特征。因此，笔者就基于这样的想法提出了一种多通道编码技术。

多通道编码技术是采用人为设置的边缘强化和表面强化卷积核，对原始图像进行卷积再编码并拼接的一种技术。其利用特点算子进行卷积形成的图像如图4所示。图5是将R通道原图与Laplace算子卷积图进行拼接之后的效果图，在灰度图上，背景显然被弱化，而图像主体则被进一步强化了。

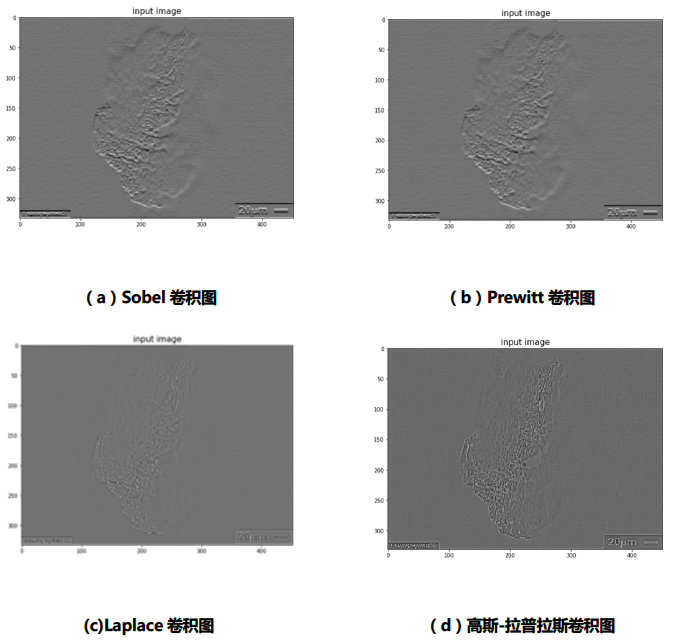
图4 采用不同边缘强化算子进行卷积后的铁谱图效果图

图5 R通道原图、Laplace算子卷积图和二者拼接后的类图

如图6采用合理的算子进行卷积可以显著的提升图像的清晰度。

图6 3通道编码并标准化图

在这个基础上，笔者构建了基于飞桨框架的CNN和ViT新模型多通道卷积神经网络（Multi-Channel Encoder Convolutional Neural Network model，简称：MCECNN）模型和多通道自注意力网络（Multi-channel Communication Self-Attention Model，简称：MCSA）模型，其模型结构大体如图7和图8。

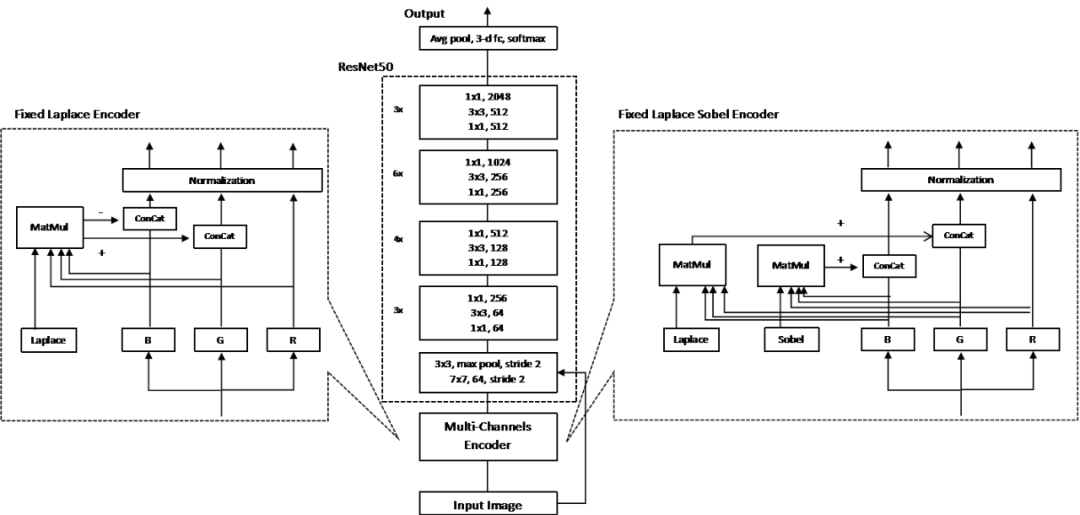
图7 MCECNN模型结构示意

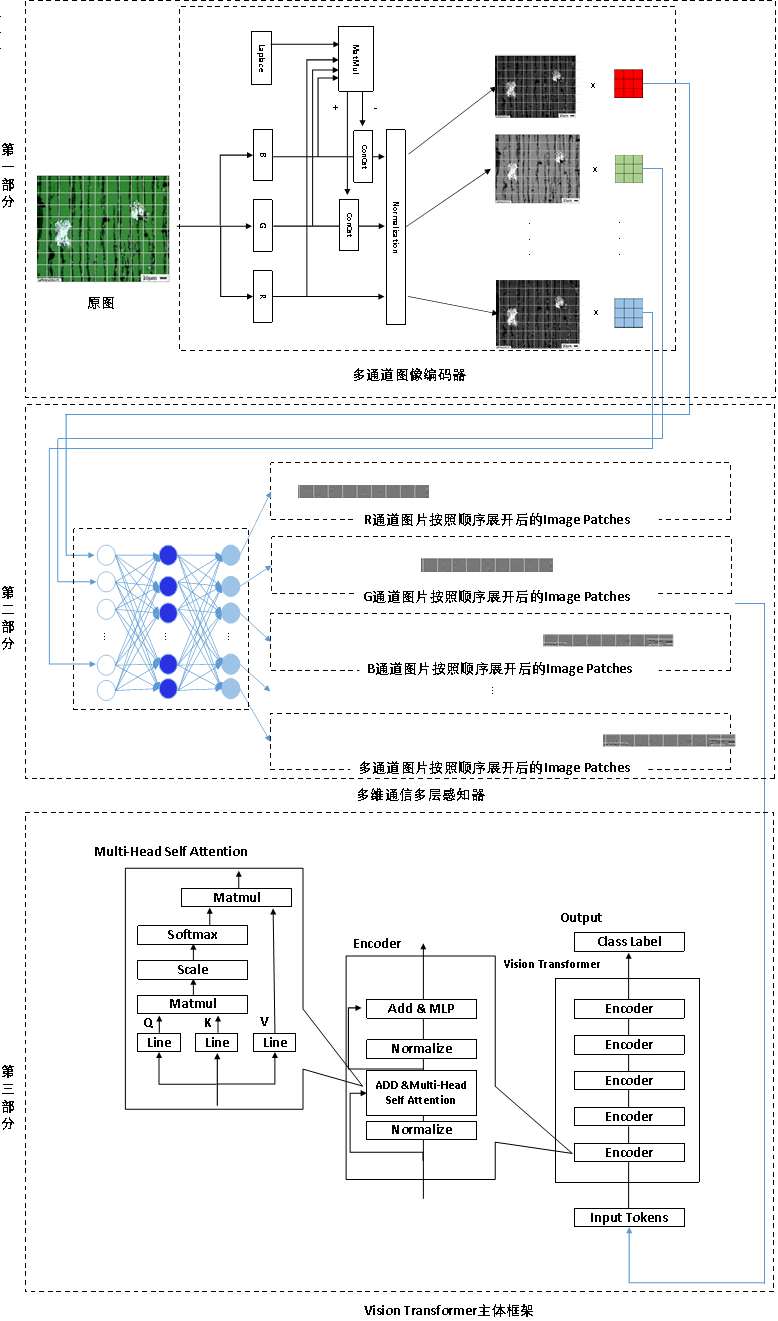
图8 MCSA模型结构示意

其比较核心的多通道编码操作主要是：

首先将图片的R（红色）、G（绿色）、B（蓝色）通道进行独立运算。

• q在B蓝色图像通道上的卷积计算过程如公式1所示：

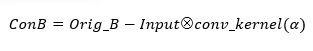
• 在G绿色图像通道上的卷积计算过程如公式2所示：

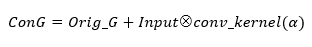
其中：

将上述卷积计算的结果，分别与G通道、B通道做加法和减法，从而降低人为干预对原图信息的影响。

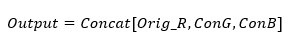
其基于飞桨进行构建的部分源码如下：

import numpy as np
import paddle
import paddle.nn as nn
from PIL import Image
import matplotlib.pyplot as plt
import matplotlib
 
class Image_combine():
    def __init__(self,img_original_path,save_path):
        self.img_original_path=img_original_path
        self.save_path=save_path
        img_original=np.array(Image.open(img_original_path))
        self.img_original_R=img_original.transpose([2,0,1])[0,:,:]#pick out the Red channel
        self.img_original_G=img_original.transpose([2,0,1])[1,:,:]#pick out the Green channel
        self.img_original_B=img_original.transpose([2,0,1])[2,:,:]#pick out the Blue channel
        self.add_original=self.img_original_R+self.img_original_G+self.img_original_B#add all channels togather
        self.min_original=self.img_original_R+self.img_original_B-self.img_original_G#R+B-G
 
    def combine_method(self,img_Laplace,img_Sobel,channel="add_original"):
        if channel=="add_original":
            img_R_1=paddle.to_tensor(self.add_original,dtype="float32").unsqueeze(0)
            img_G_1=paddle.to_tensor(self.add_original+img_Laplace,dtype="float32").unsqueeze(0)
            img_B_1=paddle.to_tensor(self.add_original-img_Laplace,dtype="float32").unsqueeze(0)
        elif channel=="add_original_confuse":
            img_R_1=paddle.to_tensor(self.add_original,dtype="float32").unsqueeze(0)
            img_G_1=paddle.to_tensor(self.add_original+img_Laplace,dtype="float32").unsqueeze(0)
            img_B_1=paddle.to_tensor(self.add_original+img_Sobel,dtype="float32").unsqueeze(0)
        elif channel=="RGB_original":
            img_R_1=paddle.to_tensor(self.img_original_R,dtype="float32").unsqueeze(0)
            img_G_1=paddle.to_tensor(self.img_original_G+img_Laplace,dtype="float32").unsqueeze(0)
            img_B_1=paddle.to_tensor(self.img_original_B-img_Laplace,dtype="float32").unsqueeze(0)                  
        elif channel=="RGB_original_confuse":
            img_R_1=paddle.to_tensor(self.img_original_R,dtype="float32").unsqueeze(0)
            img_G_1=paddle.to_tensor(self.img_original_G+img_Laplace,dtype="float32").unsqueeze(0)
            img_B_1=paddle.to_tensor(self.img_original_B+img_Sobel,dtype="float32").unsqueeze(0)     
        img_new_1=paddle.concat([img_R_1,img_G_1,img_B_1],axis=0)
        img_new_1=img_new_1.transpose([1,2,0])
        img_new_1=img_new_1.astype("int32").numpy()
        img_new_1[img_new_1>255]=255
        img_new_1[img_new_1<0]=0
        #plt.imshow(img_new_1)
        plt.imsave(self.save_path+self.img_original_path[14:-4]+"_deal_"+channel+".jpg",img_new_1/255)
        #matplotlib.image.imsave(self.save_path+self.img_original_path[15:-4]+"_deal_"+channel+".jpg",img_new_1.astype("float32"))
 
    def combine_method_test(self,img_Laplace,img_Sobel,channel="add_original"):
        if channel=="add_original":
            img_R_1=paddle.to_tensor(self.add_original,dtype="float32").unsqueeze(0)
            img_G_1=paddle.to_tensor(self.add_original+img_Laplace,dtype="float32").unsqueeze(0)
            img_B_1=paddle.to_tensor(self.add_original-img_Laplace,dtype="float32").unsqueeze(0)
        elif channel=="add_original_confuse":
            img_R_1=paddle.to_tensor(self.add_original,dtype="float32").unsqueeze(0)
            img_G_1=paddle.to_tensor(self.add_original+img_Laplace,dtype="float32").unsqueeze(0)
            img_B_1=paddle.to_tensor(self.add_original+img_Sobel,dtype="float32").unsqueeze(0)
        elif channel=="RGB_original":
            img_R_1=paddle.to_tensor(self.img_original_R,dtype="float32").unsqueeze(0)
            img_G_1=paddle.to_tensor(self.img_original_G+img_Laplace,dtype="float32").unsqueeze(0)
            img_B_1=paddle.to_tensor(self.img_original_B-img_Laplace,dtype="float32").unsqueeze(0)                  
        elif channel=="RGB_original_confuse":
            img_R_1=paddle.to_tensor(self.img_original_R,dtype="float32").unsqueeze(0)
            img_G_1=paddle.to_tensor(self.img_original_G+img_Laplace,dtype="float32").unsqueeze(0)
            img_B_1=paddle.to_tensor(self.img_original_B+img_Sobel,dtype="float32").unsqueeze(0)     
        img_new_1=paddle.concat([img_R_1,img_G_1,img_B_1],axis=0)
        img_new_1=img_new_1.transpose([1,2,0])
        img_new_1=img_new_1.astype("int32").numpy()
        img_new_1[img_new_1>255]=255
        img_new_1[img_new_1<0]=0
        plt.imshow(img_new_1)
        plt.imsave(self.save_path+self.img_original_path[14:-4]+"_deal_"+channel+".jpg",img_new_1/255)
        return img_new_1

尔后，需要将该模型前置到CNN和ViT模型的前端，实现MCECNN和MCSA两个新模型结构的构建和训练。

最后，基于迁移学习技术，笔者进行了两组新模型的多模型变体训练和对比。如图9、10、11所示，MCECNN模型（下图中标号A+B）收敛速度和其在验证集上的精度达成速度都显著得到了提升，其在测试集上的精准率和召回率也显著得到了提升，这证明多通道编码机制有效聚焦了铁谱图像故障诊断的边缘特性，在卷积技术路线上取得了该领域SOTA效果。

说明：下图的标号PURE是指基于ResNet50模型训练出来的铁谱图像智能分类模型。而其他曲线代表是不同边缘算子进行多通道编码后与ResNet50进行组合后的新模型，其中效果最优者为MCECNN模型（A+B）。

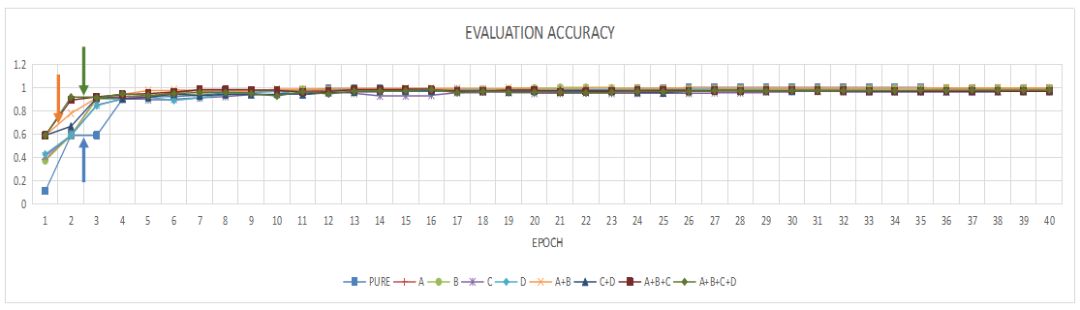
图9 MCECNN模型在验证集上的精度提升曲线

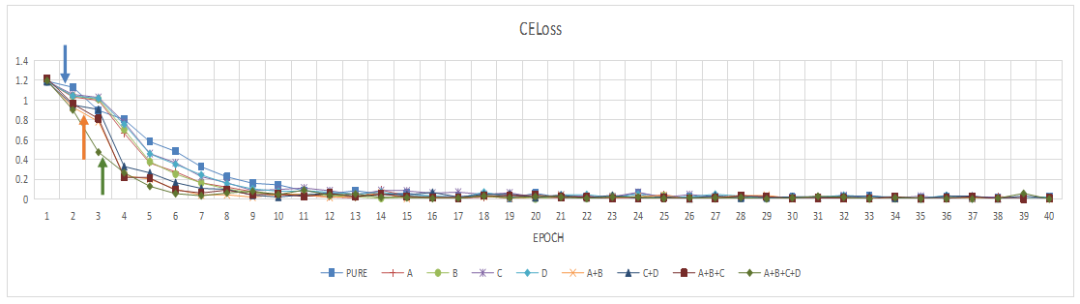
图10 MCECNN模型在训练集上的损失收敛情况

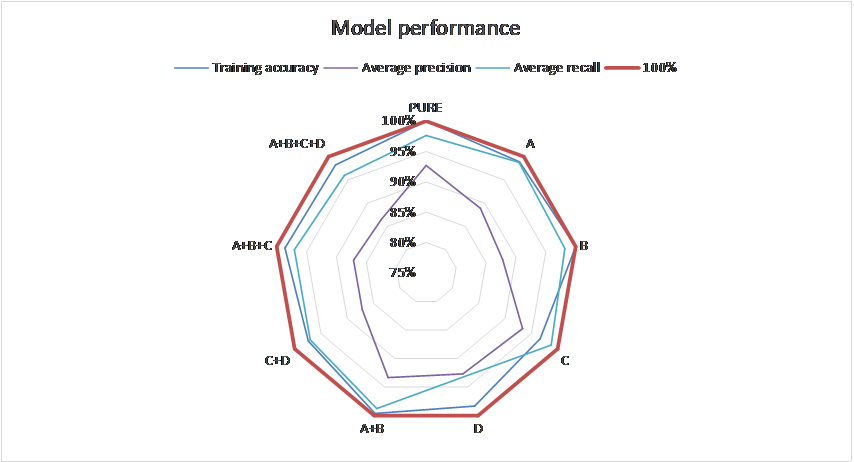
图11 MCECNN模型平均效果图

同样为了探寻Vision Transformer建模思路，笔者构建了MCSA模型（下图标示为MCSA）。如图12所示，Vision Transformer技术路线（下图标示为ViT）相较于CNN（下图标示为PURE）技术路线，其在验证集上达到较高准确率的速度更快，同时，经过引入多通道图像编码机制的MCSA模型在验证集上达到较高准确率的速度表现最佳。如图13所示，在铁谱图像故障诊断领域，Vision Transformer技术路线在机器学习的过程中，误差收敛速度整体快于CNN的技术路线，而MCSA模型则表现出了更加显著的收敛性能。

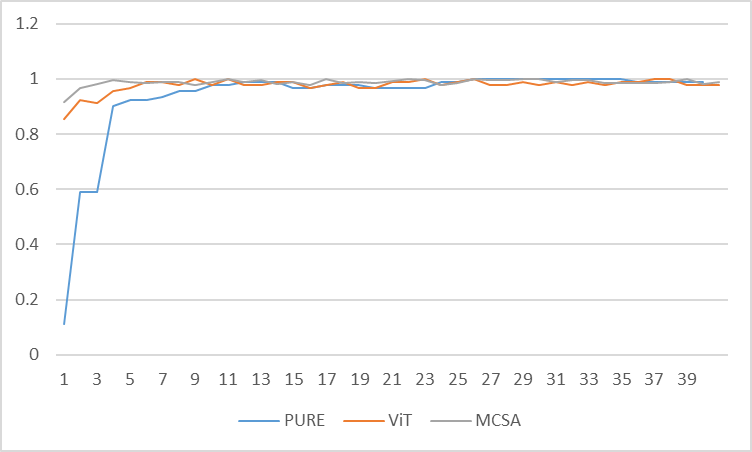
图12 各种模型在验证集上的表现

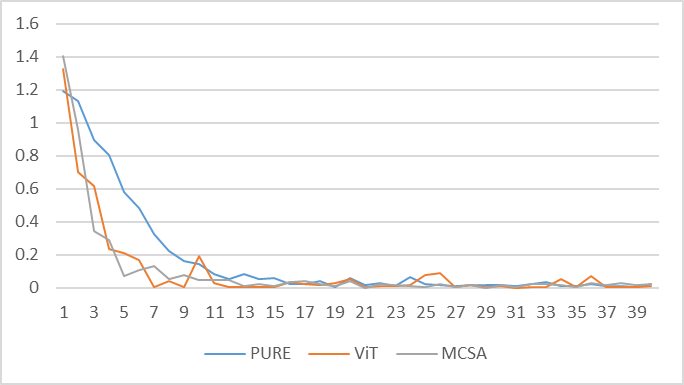
图13 各种模型在训练集上的误差收敛情况

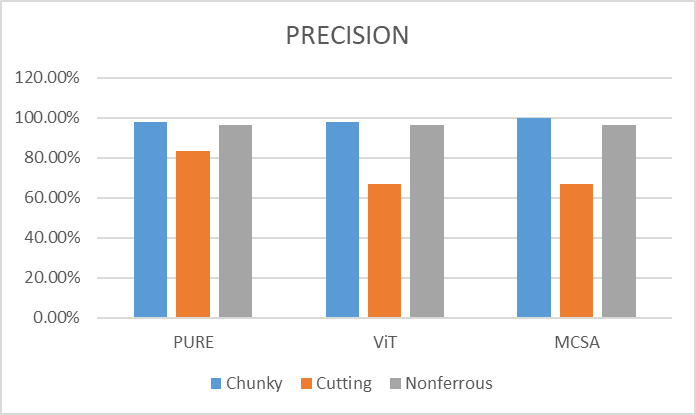
图14 各模型在测试集上的精准率

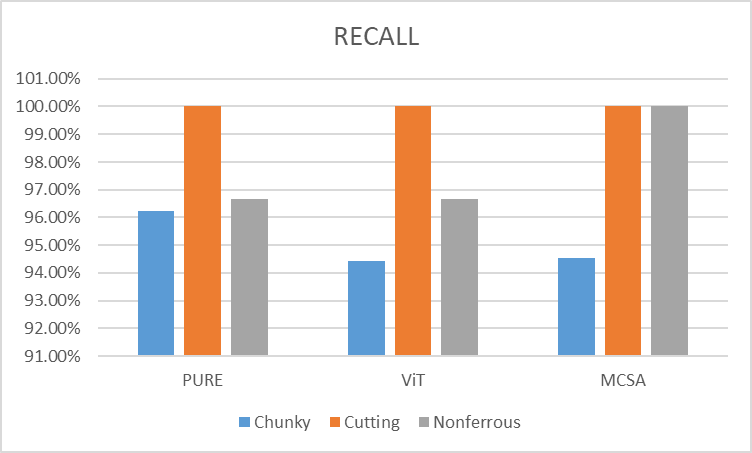
图15 各模型在测试集上的召回率

如图14所示，测试集上的精准率中MCSA在Chunky故障类（铁谱图像块状磨损颗粒物故障类）上表现更好，而在Cutting故障类（铁谱图像切削状磨损颗粒物故障类）上表现较差。如图15所示，各模型在测试集上的召回率中MCSA在Chunky故障类上表现较差，而在Cutting故障类、Nonferrous故障类（铁谱图像有色金属磨损颗粒物故障类）上表现较好。在利用Vision Transformer技术路线构建铁谱图像智能故障诊断领域，MCSA模型拥有更加强劲的性能。

限于篇幅，利用飞桨进行铁谱图像智能诊断的工作还有很多细节无法披露，例如多维通信、信息聚合机制、如何有效的衔接多通道编码技术和CNN模型、ViT模型、各种颗粒背后的故障机理等等。但是不得不说，飞桨作为一个优秀的国内深度学习框架，其完整的培训体系，清晰的系统构成，有力的技术支持，绝不输于国外任一技术框架，其为相关领域的研究提供了完整而全面的支撑，使相关基础性交叉学科的开展变得更加便捷、高效。

相关链接

• 论文：
  

https://www.sciencedirect.com/science/article/pii/S0301679X22002298

• PaddleCNN：

https://github.com/fiyen/PaddlePaddle-CNN

• PaddleViT：

https://github.com/BR-IDL/PaddleViT

关注【飞桨PaddlePaddle】公众号

获取更多技术内容~