【CSDN竞赛第五期】“三而竭”采用等比求和公式法的思考

原题题目

        一鼓作气再而衰三而竭。 小艺总是喜欢把任务分开做。小艺接到一个任务，任务的总任务量是n。 第一天小艺能完成x份任务，第二天能完成x/k ... ...第t天能完成x/(k^(t-1))。 小艺想知道自己第一天至少完成多少才能完成最后的任务。

公式推导

第一天为x份任务，即x除以1，1为k的0次方。

第二天为x/k份任务，以此类推，得到以下的公式表达：

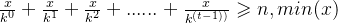
其中 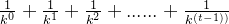可以利用高中时学的等比数列求和公式，提取x后，得到如下公式：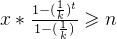

即

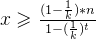
当t趋近于无穷大的时候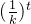，趋近于0，所以公式可以化简为: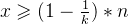

实现代码

int solution(std::vector<int>& vec){
    int n=vec[0];
    int k=vec[1];
    return n-n/k+1;
}

运行结果

仅AC了20%。

原因分析

 在题目中，其实有两个隐藏条件需要考虑：

        1、单个任务不能继续拆分为分数，所以每天完成的任务数必须为整数；

        2、每天完成的任务最小值为1。

        由于这两个隐藏条件。所以不能简单的用公式法来解这个问题，需要通过循环查找或者优化为二分查找法对查找出满足大于n的x，具体实现的方法，参考其他同学在CSDN中分享，不再赘述。

平台建议

        对于具体题目来说，题目的个体差异性比较大，不做建议。对于平台体验来说，我觉得可以做几个优化。

        1、比赛结束后，是否可以给出题目的链接，让同学们可以继续再回味总结总结；

        2、自测的时候，是否可以给出正确的运行结果，不切换IDE，解决手算验证结果慢的问题；

        3、比赛结束后，给几个参考代码实现或者思路提示，让同学们比赛后有所提高；

        4、比赛结束后，开放题目讨论区，让同学们可以讨论不同的解法和思考，提高平台活跃度。

        5、积累一定数量的勋章是否可以换个周边礼物，对我们这种小白同学也鼓励鼓励。

        总体来说，平台的IDE环境和自测框架都比较友好，如果能结合强大的博客资源整合出一个覆盖全面的计算机社区、教育、培训、认证、招聘等一体化的平台，那么对我们这些编程爱好者们应该是一个好事情吧。