超分辨率提升IRN网络

1. 介绍

IRN网络，实质就是为了解决图像还原的损失最小化（优化）的问题。（压缩后图像还原）

首先我们采样图像等信号时候是连续的，而在计算机获取时候是离散的！所以，很明显信号状态由连续变为离散，这就会有损失了，那么损失误差是不是在容许的范围内，根据采样得到离散的点能不能还原出连续的信号？这就是该理论产生的原因，它就来帮助你解决这个问题！
该采样定理的结论是：找到信号最大的频率分量，再用2倍于最大频率分量的采样频率对信号进行采样，从理论上解决了，离散信号能够重建出连续信号的问题。

2. 网络结构

• 如下网络结构图，利用小波变换把原图X分解成如图4个分量，这4个分量分别对应高频分量XH，对应三个不同方向的高频分量H(水平)、V(垂直)、D(对角)，低分部分XL，对应A。这里的低频分量与双线性插值降采样得到的低分辨率结果是一样的，而高频分量则是在降采样过程中被丢失的信息。

• 各分量输入网络中，由堆叠的缩减模块组成，每个模块都包含一小波变换模块和几个可逆神经网络模块（InvBlocks），每个缩减模块将空间分辨率降低２倍。而这些INVBlocks就是来表示”潜在变量“的，熟悉不，嘿嘿，流模型的本质呢！
  

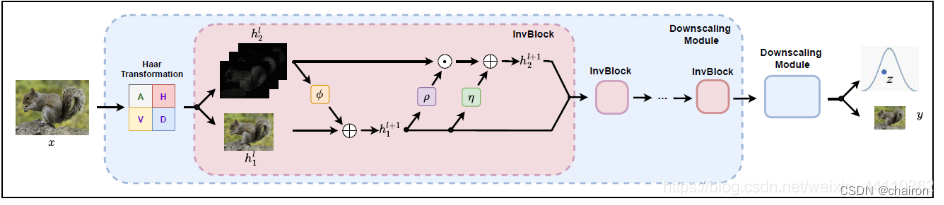
• 该可逆神经网络模块中,核心操作就是”分块耦合“！！这里采用了进化版本， Density estimation using Real NVP的仿射变换的耦合！下图就是NVP模型论文的正向缩小和反向放大的耦合原理！

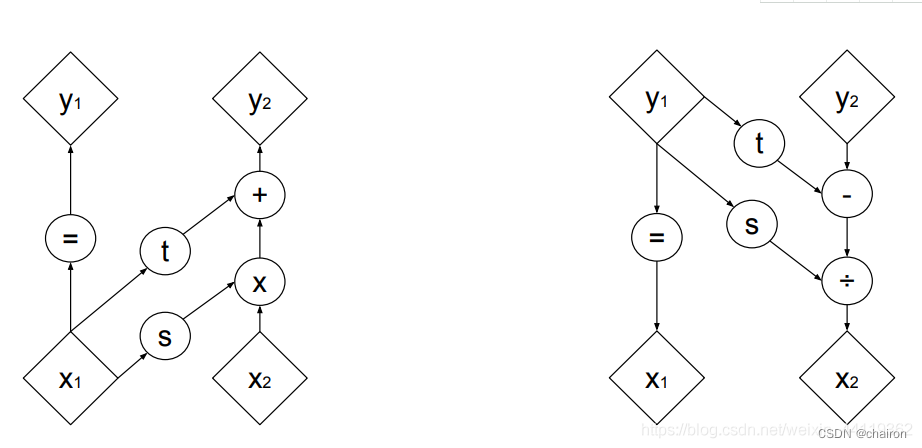
转换成公式就是很简单的一个仿射变换操作，其中里s，t 都是 x1 的向量函数，形式上第二个式子对应于 x2
的一个仿射变换，因此称为“仿射耦合层“！！！！！！！！
1
2

• 需要求解雅可比矩阵转行列式计算，该耦合层的特点还有：通过随机的方式将向量打乱，可以使信息混合得更加充分，最终的 loss 可以更低！那么在图像中呢？在网络中图像是3个维度，宽和高属于空间维度，不可分割，而通道维度是唯一可以打乱的了！
  

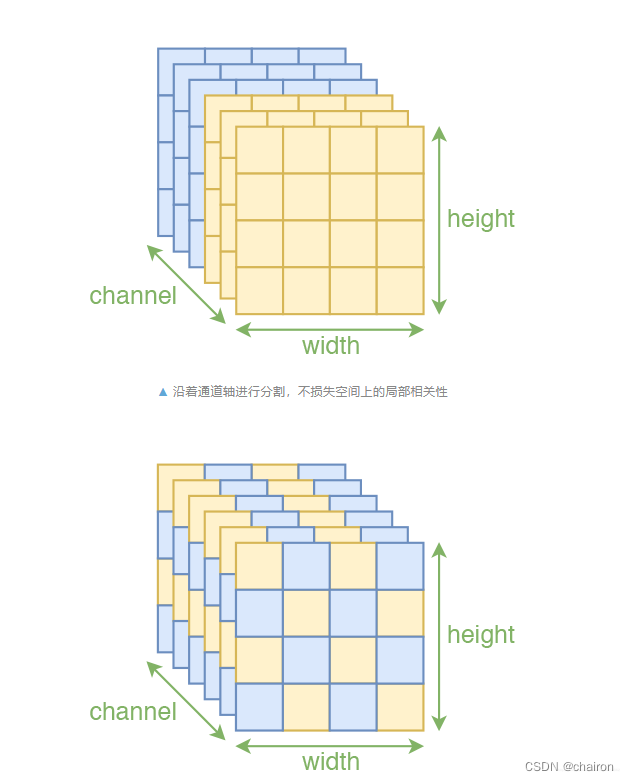
• 只对“通道”轴执行。也就是说，沿着通道将输入分割为 x1,x2 后，x1还是具有局部相关性的，还有沿着通道按着同一方式打乱整体后，空间部分的相关性依然得到保留，因此在模型 s,t 中就可以使用卷积了。这种特殊的分割也保留了空间局部相关性，论文中是两种 mask 方式交替使用的，但这种棋盘式 mask 相对复杂，也没有什么特别明显的提升，所以在 Glow 中已经被抛弃。不过想想就会发现有问题。一般的图像通道轴就只有三维，像 MNIST 这种灰度图还只有一维，怎么分割成两半？又怎么随机打乱？为了解决这个问题，RealNVP 引入了称为 squeeze 的操作，来让通道轴具有更高的维度。（类似于Focus操作）
  

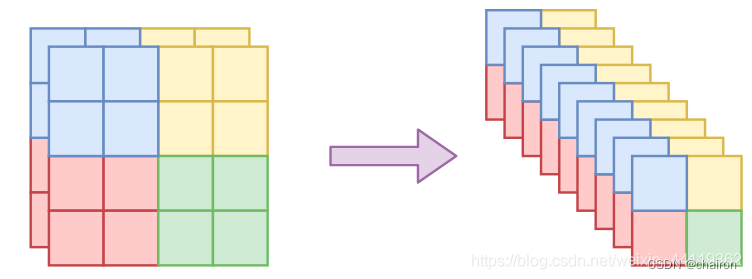
• 在RealNVP中，使用了最终形态的打乱信息:squeeze 的操作，来让通道轴具有更高的维度。有了 squeeze 这个操作，我们就可以增加通道轴的维数，但依然保留局部相关性，从而我们前面说的所有事情都可以进行下去了，所以 squeeze 成为 flow 模型在图像应用中的必备操作。

3.网络正向和反向输出

1. 回到网络正向传输缩小过程中，在通过可逆缩放网络Blocks后，生成了FLOW模型的必备可逆函数$f$，该函数由两部分表示：

   1. ”潜在变量“$Z$，服从正态分布的变量，
   2. 产物图像$y$是一个新的图像。

2. 反过来逆放大过程中，通过可逆函数$f$，将$y$和$Z$拟合成新图$X$”！！

3. 其损失自然就是模拟分布重建图(sR)和原始(HR)X的损失了！
   

    损失函数：采用重建损失，就是正向输出的缩小图$y$指导损失和分布匹配损失(逆转放大后的方法图$X$)的加权和。
   1

IRN论文实验图，结果很好，改善明显！IRN+：在IRN基础上加入感知损失！

5. 参考文献

参考文献