接着上一次普林斯顿微积分读本03第二章--编程实现函数图像绘制、三角学回顾继续往下，经过前面的几个基础的夯实之后，终于进入高数章节的学习了，之前我其实已经温习过一遍了，怎么说呢，这块对我来说还是有点难的，希望通过这次一点一滴地输出来攻克它们，下面正式开始。

极限：基本思想：

如书本所述：“如果没有极限的概念，那么微积分将不复存在。”，可见学好极限是非常有必要的，接下来则从它的基本思想开始入手。

极限从一个奇怪的概述开始：“我们从某个函数f和x轴上的一点出发，该点称为a，需要理解的是：当x非常非常接近于a，但不等于a时，f(x)是什么样子的？”，其实这句就道出了极限它研究的东东，x是一个趋向的值，而非一个确定的值，这个就跟普通的函数研究的点就不一样了。

这里举一个例子：f(x) = x - 1，其中f的定义域是：

这个是啥意思知道不，它的意思是除2以外的所有实数，我们就可以这样表示：

f(x) = x - 1   当x ≠ 2。

是不是这个函数比较古怪，居然将2从定义域中去除掉了，其实在之后的学习中可以看到,f它是一个有理函数，目前先不管这么多，接受这种定义既可，其图像为：

那么问一下：f(2)是多少呢？大多数人可能很容易回答f(2)=1，但是！！！它不在定义域里头哟，所以最好的回答应该是f(2)是无定义的。

而换一个角度，其实可以给x找一些接近于2的值，你会发现f(x)的值也会接近于1，比如：f(2.01) = 1.01、f(1.999) = 0.999。

对于这样的函数，其实在数学上是用这样的式子来表示它的：

这其实也就是极限的引出，其中lim是limit的缩写，该式子表示“当x趋于2，f(x)的极限等于1”，等于极限研究的角度跟函数的完全不一样的，函数研究的是一个精确的值，而极限研究的是一个近似值【它描述了函数在一个定点附近的行为】，对于极限还有另一种表示法：

这种写法在实际计算时用得比较少，不过它的意义比上面lim的那种方式要清晰：当x沿着数轴从左侧或者从右侧趋近于2时，f(x)的值会非常非常接近于1（并保持接近的状态）。

下面再定义一个分段函数，该函数的定义域是所有实数，如下：

图像对应于：

那么问一下：

它是什么？

虽说g(2)=3,但也还有：

因为：

其实就是之前我们定义的：

另外有一个认知上的注意点：等式左边它不是x的函数，它表达的是当x接近于2时，f(x)接近于1，这种认知的转变还是非常重要的。

另外我们可以将x替换成任意字母，比如：

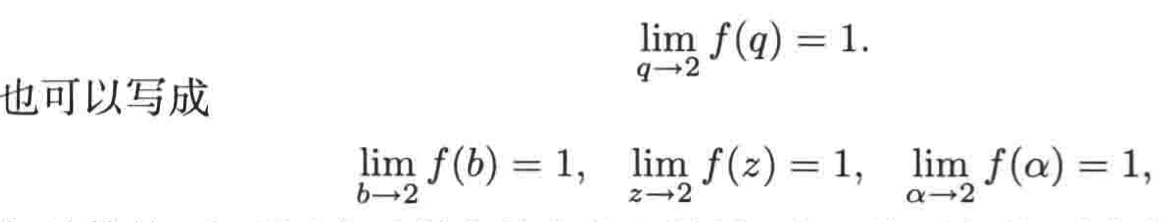
但是有一个要点就是：在极限中，变量x只是一个虚拟变量【也就是不是一个精确值】，它是一个暂时的标记；另外当你求出极限的值时，结果不可能包含这个虚拟变量。

左极限和右极限：

对于极限还是分方向的，也就是左极限和右极限，先来从这个图来引出左右极限的概念，我觉得举的这个例子还是相当贴切的：

其中看到小人了木有，相当于在走山路，那看图请问：你如何描述h(x)在x=3附近的行为？

由于研究的是趋于极限的行为，很明显这个h(3)=2的这个就不必要研究了：

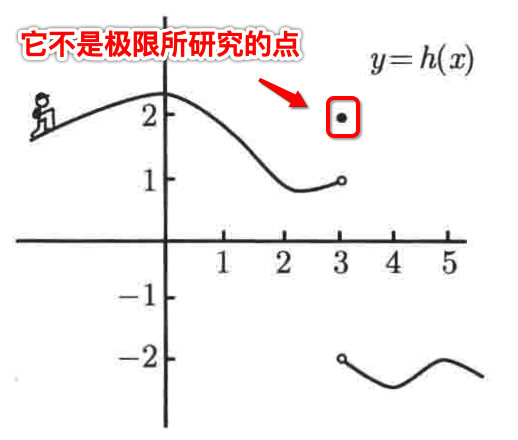
左极限：

好，接下来先从左侧接近于x=3的情况，很明显这个人如果从左侧走到快接近于3的位置时，此时所在的山的高度就会接近于1对吧，而如果你走到3的位置，由于是无路的，那么你会陡然坠落（因为不能是3），而x=3的右侧的值也都是走不到的，所以此时就可以说h(x)在x=3的左极限等于1。

右极限：

换一个方向走，你从图的右边往左走，当你走到接近于3时，山的高度就会接近于-2，此时对于3及左侧的值都是无关紧要的，所以此时就可以说：h(x)在x=3的右极限等于-2。 

总结：

此时对于左右极限就有如下表示法了：

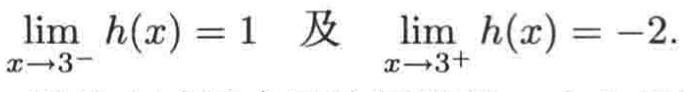
其中极限中3后的小减号表示该极限是一个左极限；3后的+号表示该极限是一个右极限，注意，这个符合一定是在3后面写，不要在3前面加，比如如果写成这样意义就变了：

这个很明显是表示h(x)在x=-3时的通常的双侧极限【关于这个词待会就会统一总结】。

另外再说一点：

表示此极限只涉及到小于3的x值，也就是说，你需要在3上减一点点来看会有什么情况发生；类似的：

表示此极限只涉及到大于3的x值，也就是说，你需要在3上加一点点来看会有什么情况发生。

双侧极限、左极限、右极限关系：

通常我们写极限可能不会看到有写+-符号的对吧，比如：

这种就叫双侧极限，也就是它的左极限和右极限在x=2处都存在且相等，用数学语言来描述就是：

如果左极限和右极限不相等，那么双侧极限就不存在哟，我们就可以写作：

其中“不存在”也可以用数学字母来表示：DNE(Does Not Exist)。

何时不存在极限：

双侧极限不存在的情况：

现在我们知道了如果左右极限不相等时那么双侧极限也就不存在了对吧，下面举一个这样的例子，f(x) = 1/x，它的函数图像我们在之前的学习中也接触过了，如下：

那：

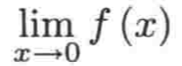
它是多少呢？先求一下右极限：

也就是当x是正的且接近于0时，f(x)的值越来越大，最终趋于正无穷在大，接下来再来看一下左极限：

它趋于负无穷大。

而由于左右极限不相等，所以：

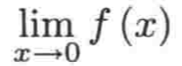
双侧极限显然不存在。

下面再来看另一个函数的极限：

它的函数图像：

很明显此函数在x=0处的左右极限都是∞，因此可以说：

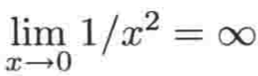
垂直渐近线：

接下来就可以引出“垂直渐近线”的正式定义了：

“f在x = a处有一条垂直渐近线”说的是：

其中至少有一个极限是∞或-∞。

左右极限不存在的情况：

在上面咱们只讨论了双侧极限不存在的情况（也就是只要证明左右极限不一样就可以了），但是有木有可能出现左极限或者右极限不存在的情况呢？答案是肯定的，看下面这个函数：

由于sin(x)在x=π，2π， 3π，....上的值全为0，为啥？拿sin(π)来说，它可以转换为sin(π/2+π/2)，而又可以化为：sin(π/2)cos(π/2)+sin(π/2)cos(π/2)，因为sin(π/2)=1，cos(π/2)=0，所以sin(π/2)cos(π/2)=1*0=0，所以sin(π/2)cos(π/2)+sin(π/2)cos(π/2)=0+0=0，所以sinπ等于0。其它的就类似，我们取其倒数，会发现sin(1/x)在1/π，1/2π， 1/3π，....上的值也全为0，而这些x的取值就是在x轴上的截距，如下：

也就是接近于0的时候，这些x轴的点它们都挤到一起了，由于在每一个x轴截距之间，sin(x)向上走到1或向下走到-1，因为sin(1/x)也是一样，将其画出来就是：

那么它的右极限是什么呢？

由于图像在x=0附近很杂乱，它无限地在1和-1之间震荡，当你从右侧向x=0处移动时，振荡会越来越快，这里没有垂直渐近线，也没有极限。当x从右侧趋于x=0时，该函数不趋于任何数，所以它的右极限是不存在的（DNE）。

在∞和-∞处的极限：

目前我们已经研究了在接近某一点x=a时的函数行为对吧，如我们所见过的极限的定义：

但是有时候我们需要理解当x变得非常大的时候，一个函数的行为是如何的。换言之，就是对变量x趋于∞时函数的行为，也就是极限的式子如：

它表示f的图像在y=L处有一条右侧水平渐近线，同样类似的，当x趋于-∞时，极限的式子如：

表示当x变得越来越负时，f(x)会变得非常接近于值L，并保持接近的状态，此时它对应于函数y = f(x)的图像有一条左侧水平渐近线。所以可以把这些转化为如下定义：

这里有两个对立的情况会出现：

1、有些函数没有任何水平渐近线，比如y = x^2，因为当x变得越来越大的时候，y值只会无限上升，所以它的极限情况是：

2、有些函数极限是不存在的，这个其实在上面已经探讨过了，比如：

它会越来越接近某个值，但是只是在-1和1之间来回振荡，所以此函数木有水平渐近线，也不会趋于∞或-∞，所以它的极限是不存在的。

接下来回到上面看到的这个函数上来：

当时我们只考虑了x趋于0点的情况：

接下来我们来考虑x变得非常大的情况，首先当x很大时，1/x也是非常接近于0的对吧，由于sin(0) = 0，所以sin(1/x)就会非常接近于0，所以：

所以我们就可以向右扩展y=sin(1/x)的图像了，而由于这个函数是一个奇函数，证明如下：

所以，此时我们就可以把图像左右扩成这样了：

大的数和小的数：

接下来需要讨论一个关于大数和小数的问题，这块也是比较容易搞错的。

对于这两个数：1 000 000 000 000和 -1 000 000 000 000，你觉得哪个是大的数，哪个是小的数呢？

对于这两个数：0.000 000 001和-0.000 000 001，你觉得它又是大的数还是小的数呢？

下面给出一个非正式的定义：

• 如果一个数的绝对值是非常大的数，则这个数就是大的；
• 如果一个数非常接近于0（但不是真的等于0），则这个数就是小的；

 其中“非常大”和“非常接近于0”分别意味着什么呢？下面拿这个极限来说：

也就是当x是一个足够大的数时，f(x)的值就会几乎等于L，可问题是：多大才是“足够大”呢？这其实就需要取决于你想让f(x)的距离L有多近，这里举两种情况你就知道在说啥了：

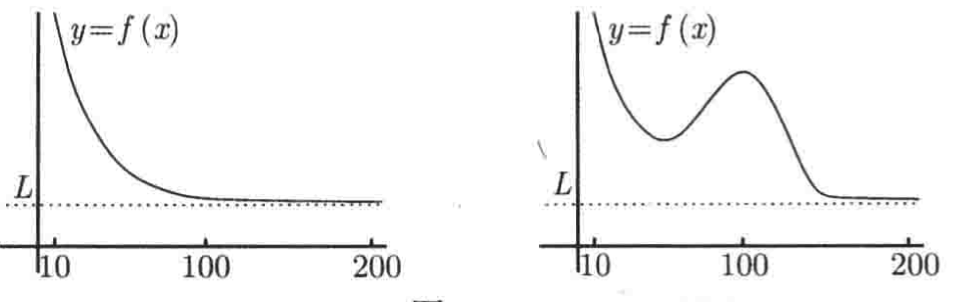
可以看到，左图在当x至少是100时，f(x)看上去非常接近于L，此时任何比100大的数都是“大的数”；而右图，对于100就不是大的数了，可能得要到200才是一个大的数。一定要体会到，这个大的数是需要取决于f(x)的距离L有多近来决定的，你不能说1 000 000 000 000这样的数就已经很大了，因为有可能函数要到5 000 000 000 000才变得趋于它的水平渐近线。

而在极限描述中，会经常使用术语“在∞附近”来代替“大的正的数”（在字面意义上说，一个数不可能真的在∞附近，因为∞无穷元，不过在x -> ∞时的极限语境中，“在∞附近”的说法还是说得通的），同样也可以用“在-∞附近”来强调我们所指的“大的负的数”。

同样，对于小的数，也同样需要结合某个函数或极限的语境来考虑，比如我们经常会看到的极限：

关于渐近线的两个常见误解：

接下来了解一下关于渐近线的两个常见的误区：

1、一个函数不一定要在左右两边有相同的水平渐近线：

比如我们在上面学习的f(x) = 1/x的图像，左右两侧都有y=0这条水平渐近线对吧：

也就是：

然而，对于这样的函数：

它的图像其实是：

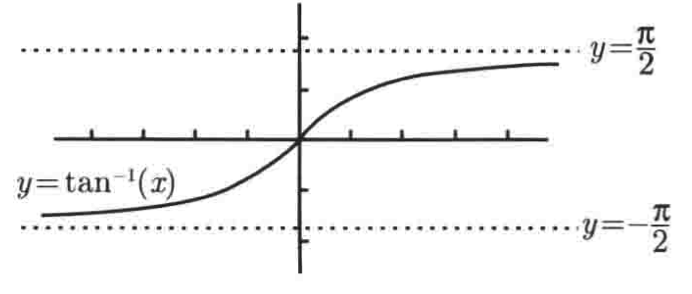
它在y=π/2处有一个右侧水平渐近线，而在y = -π/2处有一条左侧水平渐近线，很明显左右渐近线不同对吧，用极限表示就是：

也就是你需要纠正这样的认知：

一个函数的确可以有不同的右侧和左侧水平渐近线，但是最多只能有两条水平渐近线（一条在右侧，另一条在左侧）；也有可能一条都没有；或者只有一条。

比如：

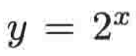
它就有一条左侧水平渐近线，但是没有右侧水平渐近线：

跟垂直渐近线是相反的：一个函数可以有多条垂直渐近线（比如y = tan(x)，它有无穷多条垂直渐近线）。 

2、一个函数不可能和它的渐近线相交：

对于渐近线我们通常的理解是一条函数越来越接近但永远不会相交的直线，其实这是一个误区，这里举一个这个函数：

f(x) = sin(x) / x，它的图像为：

由于sin(x)的值是在-1和1之间震荡，因此sin(x)/x的值在曲线y = -1/x和y=1/x之间振荡。图中用的虚线表示的曲线y = 1/x和y = -1/x形成了正弦波的包络，也就是：

也就是x轴是f函数的水平渐近线，其中是不是可以看到这个水平渐近线和函数图像是不是反复在相交呀？

关于这个极限的证明，需要接下来学习的三明治定理（俗称的“夹逼定理”）。

三明治定理：

定义：

三明治定理，又名夹逼定理，说的是：如果一个函数f被夹在函数g和h之间，当x->a时，这两个函数g和h都收敛于同一个极限L，那么当x->a时，f也收敛于极限L。

看一下图可能就明白了：

理解：

假设对于所有的在a附近的x，我们都有g(x)≤f(x)≤h(x)，既f(x)被夹在g(x)和h(x)之间，此外还假设：

那么就有这个结论：

既当x->a时，所有三个函数都有相同的极限。

对于单侧极限，也有类似版本的三明治定理，只是这时不等式g(x)≤f(x)≤h(x)仅在a的我们心的一侧成立，比如：

其中y = xsin(1/x)的图像和y=sin(1/x)的图像是很相似的，只是前面有一个x使得函数陷于y=x和y = -x之间，比如下图所示：

从图中可以看出，当x趋于0时，函数仍旧有激烈的震荡，但是现在它们被包络线抵制着，关于啥是包络线，这里百度百科一下：

还是有点一知半解，网上找到一个这样的gif，感受一下包络线：

也就是函数g是下方的包络线y = -x，而函数h是上方的包络线y = x，这是要求极限：

其实它正好是三明治定理的的一个完美应用，我们只需要证明对于x>0，有g(x)≤f(x)≤h(x)，那要怎么来证明呢？这里需要用到任意数的正弦都是处于-1和1之间的对吧，所以：

-1≤sin(1/x)≤1

此时用x乘以这个不等式，就有：

-x≤xsin(1/x)≤x，这正好就是我们需要的g(x)≤f(x)≤h(x)，而还有：

因此，当：

夹逼的函数g(x)和h(x)的值收敛于同一个数0，所以f(x)也一样，也就证明了：

但是！！！要注意：如果没有前面的因子x，上式显示不成立，因为在之前我们也证明了：

证明上节的极限情况：

学习了夹逼定理之后，我们就可以对上节最后的这个极限进行一个证明了，还记得那个极限不，回忆一下：

为了证明此式，需要用到的三明治定理一个稍有不同的形式，涉及在∞处的极限，这个跟之前的不太一样，也就是对于所有的很大的x，都有：

g(x)≤f(x)≤h(x)，其定义跟有限处极限的三明治定理几乎是一模一样的，所以用到对于所有的x，都有：

-1≤sin(1/x)≤1，但是这次x>0，然后不等式都除以x，为：

现在令x->∞，由于-1/x和1/x的权限都是0，sin(x)/x的极限也必为0，也就是说由于：

也必有：

总结：

对于夹逼定理其实它说的就是：

这也适合左极限或右极限，在那种情况下，不等式只需要在a的相应一侧对于x成立既可；当a是∞或-∞时它也适用，在那种情况下，要求对于所有的非常大的（分别是正的或负的）x，不等式成立。

极限的基本类型小结：

我们已经看过了权限的多种基本类型了，下面来看一些各种基本类型的代表性的图像，以后有需要可以回过头来查一下：

1、在x=a时的右极限：

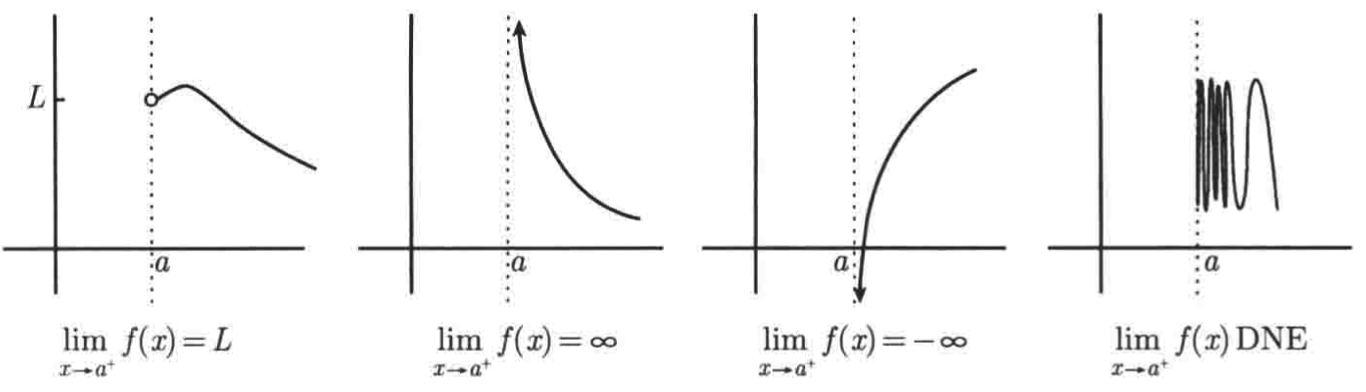
其中可以看到，这时在x=a的左侧以及x=a处f(x)的行为是无关紧要的，也就是说，当讨论右权限时，对于x≤a，f(x)取何值都不要紧，事实上，对于x≤a，f(x)甚至不需要被定义。

2、在x=a时的左极限：

这时在x=a的右侧以及x=a处f(x)的行为是无关紧要的。 

3、在x=a时的双侧极限：

左图中的左极限和右极限都存在，但是不相等，所以它的双侧极限就不存在；

而右图中的左右极限存在并相等，所以它的双侧极限存在。

其中f(a)的值是无关紧要的。

4、在x->∞时的极限：

5、在x->-∞时的权限：

编程来进行极限求解：

好，回到最亲切的环节，就是利用python来看如何来求极限，这个对于我们实际来说才是比较有意义的，毕竟完全自己手动来求解还是比较费劲的，能交给电脑的干嘛不交给电脑呢，尤其像我这种面临工作考核的，使用编程来解决数学问题是非常好的工具，下面来看一下，打算以这个极限的求解为例：

具体编程其实也很简单：

1、定义函数：

这里如何定义这个函数呢，如下：

其中x = sp.Symbol('x')相当于定义了一个书本中说的虚拟变量：

其中sympy库是一个非常强大的数学库，网上搜了一下它，感受一下它的强大：

所以对于程序员而言，需要善用它。

2、求极限：

接下来就来求一下极限：

运行：

跟书中的求解是一样的。

画出函数的图像：

接下来咱们来把此函数的图像画出来：

此时运行看一下：

是不是跟书本上的图差不多，只是这边没有限制x>0。

总结：

好了，整个章节已经学完了，涉及到的概率还是蛮多的，主要是比较抽象，需要好好的吸收和消化，因为接下来的知识只有越来越难的。