哈夫曼树的定义、原理及哈夫曼编码

1 哈夫曼树的定义与原理

 在如今素质教育的实际学习生活中，学生的成绩在5个等级上的分布规律如下：

 采用传统方法判断学生学习等级如图所示：

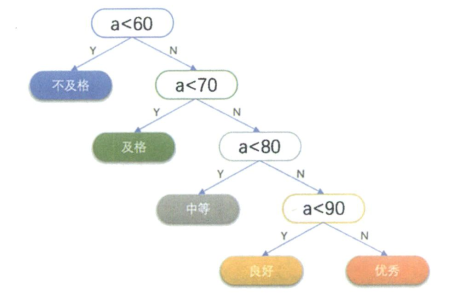
 那么70分以上大约占总数80%的成绩都需要经过3次以上的判断才可以得到结果，这显然对算力具有很大的浪费。我们对这棵二叉树重新进行分配，改成如图所示的二叉树。

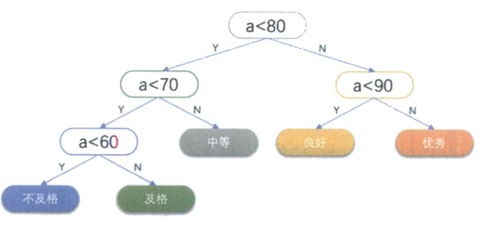
 我们把这棵二叉树简化成叶子结点带权的二叉树**（树结点间的边相关的树叫做权【weight】）**，如图所示，其中A表示不及格，B表示及格，C表示中等，D表示良好，E表示优秀。每个叶子的分支线上的数字就是五级分制的成绩所占的百分比。

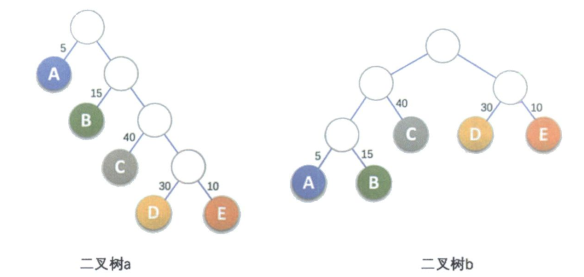
 **从树中一个结点到另一个结点之间的分支构成两个结点之间的路径，路径上的分支数目称作路径长度。**在上图二叉树a中，根结点到结点D的路径长度就为4，第二个二叉树中根结点到结点D的路径长度为2。

 **树的路径长度就是从树根到每一结点的路径长度之和。**在上图中，我们可计算出二叉树a的路径长度为$1+1+2+2+3+3+4+4=20$，二叉树b的路径长度为$1+2+3+3+2+1+2+2=16$

 结点的带权的路径长度为从该结点到树根之间的路径长度与结点上权的乘积，其中带权路径长度$WPL$最小的二叉树称做哈夫曼树。

 对上图二叉树a和b两棵树的$WPL$值：

 二叉树a的$WPL=5\times 1+15\times 2+40\times 3+30\times 4+10\times 4=315$

 二叉树b的$WPL$