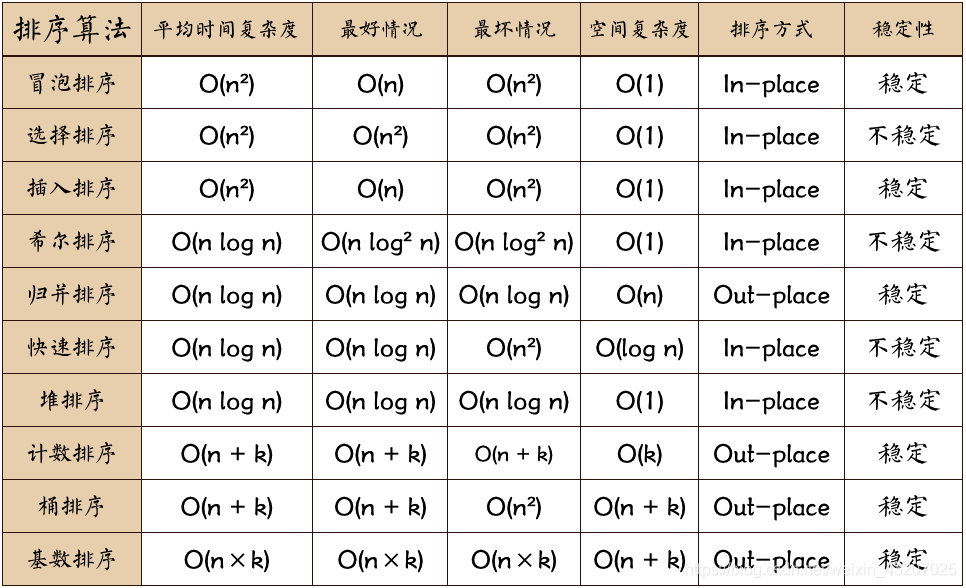
七大排序。。。

• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；
• 不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；
• 内排序：所有排序操作都在内存中完成；
• 外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；
• 时间复杂度： 一个算法执行所耗费的时间。
• 空间复杂度：运行完一个程序所需内存的大小。

稳定的排序：冒泡排序，插入排序，归并排序
不稳定的排序：选择排序，堆排序，快速排序，希尔排序

平均时间复杂度T(n) = O(nlogn)：希尔排序，归并排序，快速排序，堆排序
平均时间复杂度T(n) = O(n²)：冒泡排序，简单选择排序，插入排序

最好时间复杂度T(n) = O(n)：冒泡排序，插入排序
最好时间复杂度T(n) = O(nlogn)：归并排序，快速排序，堆排序
最好时间复杂度T(n) = O(n²)：简单选择排序

最坏时间复杂度T(n) = O(nlogn)：归并排序，堆排序
最坏时间复杂度T(n) = O(n²)：冒泡排序，简单选择排序，插入排序，快速排序

空间复杂度O(1)：冒泡排序，简单选择排序，插入排序，希尔排序，堆排序
空间复杂度O(n)：归并排序
空间复杂度O(nlogn)：快速排序

（1）当数据规模较小时候，可以使用简单的直接插入排序或者直接选择排序。

（2）当文件的初态已经基本有序，可以用直接插入排序和冒泡排序。

（3）当数据规模较大时，应用速度最快的排序算法，可以考虑使用快速排序。当记录随机分布的时候，快速排序平均时间最短，但是出现最坏的情况，这个时候的时间复杂度是O(n^2)，且递归深度为n,所需的占空间为O(n)。

（4）堆排序不会出现快排那样最坏情况，且堆排序所需的辅助空间比快排要少，但是这两种算法都不是稳定的，要求排序时是稳定的，可以考虑用归并排序。

（5）归并排序可以用于内部排序，也可以使用于外部排序。在外部排序时，通常采用多路归并，并且通过解决长顺串的合并，缠上长的初始串，提高主机与外设并行能力等，以减少访问外存额外次数，提高外排的效率。

#include <iostream>
#include <vector>
#include <algorithm>
#include <numeric>
#include <stdio.h>
using namespace std;
void heapy(vector<int> &nums, int st, int en)
{
    int dad = st;
    int son = dad * 2 + 1;
    while (son <= en)
    {
        if (son <= en - 1 && nums[son] < nums[son + 1])
            son++;
        if (nums[dad] > nums[son])
            return;
        else
        {
            swap(nums[dad], nums[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}
void heapysort(vector<int> &nums)
{
    int n = nums.size();
    for (int i = n / 2 - 1; i >= 0; --i)
        heapy(nums, i, n - 1);
    for (int i = n - 1; i > 0; --i)
    {
        swap(nums[i], nums[0]);
        heapy(nums, 0, i - 1);
    }
}
 
void maopaosort(vector<int> &nums)
{
    for (int i = 0; i < nums.size(); ++i)
        for (int j = 0; j < nums.size() - i - 1; ++j)
            if (nums[j] > nums[j + 1])
                swap(nums[j], nums[j + 1]);
}
void selsort(vector<int> &nums)
{
    for (int i = 0; i < nums.size(); ++i)
    {
        int id = i;
        for (int j = i + 1; j < nums.size(); ++j)
        {
            if (nums[j] < nums[id])
                id = j;
        }
        swap(nums[i], nums[id]);
    }
}
void insertsort(vector<int> &nums)
{
    for (int i = 1; i < nums.size(); ++i)
    {
        if (nums[i] < nums[i - 1])
        {
            int id = i - 1;
            int min = nums[i];
            while (id >= 0 && nums[id] > min)
            {
                nums[id + 1] = nums[id];
                id--;
            }
            nums[id + 1] = min;
        }
    }
}
 
int Paritition1(vector<int> &A, int low, int high)
{
    int pivot = A[low];
    while (low < high)
    {
        while (low < high && A[high] >= pivot)
        {
            --high;
        }
        A[low] = A[high];
        while (low < high && A[low] <= pivot)
        {
            ++low;
        }
        A[high] = A[low];
    }
    A[low] = pivot;
    return low;
}
 
void QuickSort(vector<int> &A, int low, int high) //快排母函数
{
    if (low < high)
    {
        int pivot = Paritition1(A, low, high);
        QuickSort(A, low, pivot - 1);
        QuickSort(A, pivot + 1, high);
    }
}
void shell_sort(vector<int> &array)
{
    int h = 1;
    int length = array.size();
    while (h < length / 3)
    {
        h = 3 * h + 1;
    }
    while (h >= 1)
    {
        for (int i = h; i < length; i++)
            for (int j = i; j >= h && array[j] < array[j - h]; j -= h)
                swap(array[j], array[j - h]);
        h = h / 3;
    }
}
void mergeSortCore(vector<int> &data, vector<int> &dataTemp, int low, int high)
{
    if (low >= high)
        return;
    int len = high - low, mid = low + len / 2;
    int start1 = low, end1 = mid, start2 = mid + 1, end2 = high;
    mergeSortCore(data, dataTemp, start1, end1);
    mergeSortCore(data, dataTemp, start2, end2);
    int index = low;
    while (start1 <= end1 && start2 <= end2)
    {
        dataTemp[index++] = data[start1] < data[start2] ? data[start1++] : data[start2++];
    }
    while (start1 <= end1)
    {
        dataTemp[index++] = data[start1++];
    }
    while (start2 <= end2)
    {
        dataTemp[index++] = data[start2++];
    }
    for (index = low; index <= high; ++index)
    {
        data[index] = dataTemp[index];
    }
}
void mergeSort(vector<int> &data)
{
    int len = data.size();
    vector<int> dataTemp(len, 0);
    mergeSortCore(data, dataTemp, 0, len - 1);
}
void printvec(vector<int> nums)
{
    for (int i : nums)
    {
        cout << i << " ";
    }
    cout << endl;
}
int main()
{
    vector<int> a = {1, 2, 1, 0, 5};
    //    heapysort(a);
    // maopaosort(a);
    // selsort(a);
    mergeSort(a);
    printvec(a);
}