自动控制原理9.3---线性定常系统的反馈结构及状态观测器

参考书籍：《自动控制原理》(第七版).胡寿松主编.
《自动控制原理PDF版下载》

---

---

3.线性定常系统的反馈结果及状态观测器

3.1 线性定常系统常用反馈结构及其对系统特性的影响

3.1.1 常用的两种反馈结构

在系统综合设计中，两种常用的反馈形式是线性直接状态反馈和线性非动态输出反馈，简称状态反馈和输出反馈；

1. 状态反馈

   设有$n$维线性定常系统：
   $$\dot{x}=Ax+Bu,y=Cx$$
   式中：$x、u、y$分别为$n$维、$p$维和$q$维向量；$A、B、C$分别为$n\times n、n\times p、q\times n$实数矩阵；

   当将系统的控制量$u$取为状态变量的线性函数：
   $$u=v-Kx$$
   称为线性直接状态反馈，简称状态反馈，其中$v$为$p$维参考输入向量，$K$为$(p\times n)$维实反馈增益矩阵；

   综合可得状态反馈系统动态方程：
   $$\dot{x}=(A-BK)x+Bv,y=Cx$$
   其传递函数矩阵为：
   $$G_K(s)=C(sI-A+BK{)}^{-1}B$$
   加入状态反馈后系统方块图如下图所示：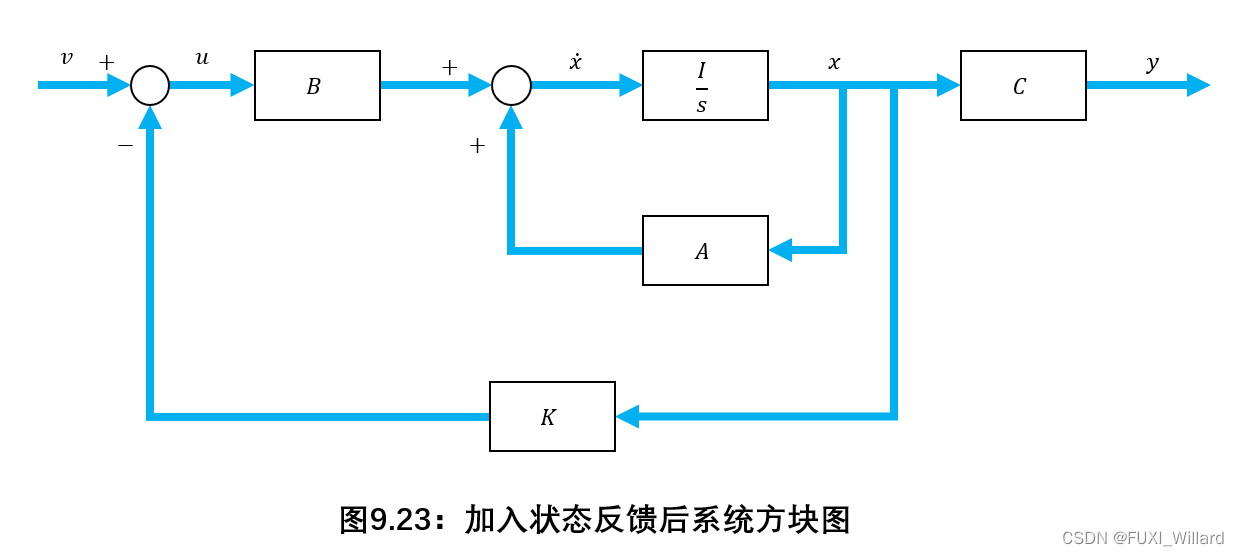

   

2. 输出反馈

   输出反馈的目的：使系统闭环成为稳定系统，然后在此基础上进一步改善闭环系统性能；

   输出反馈的两种形式：一种是将输出量反馈至状态微分，另一种是将输出量反馈至参考输入；

   输出量反馈至状态微分系统方块图如下图所示：

   

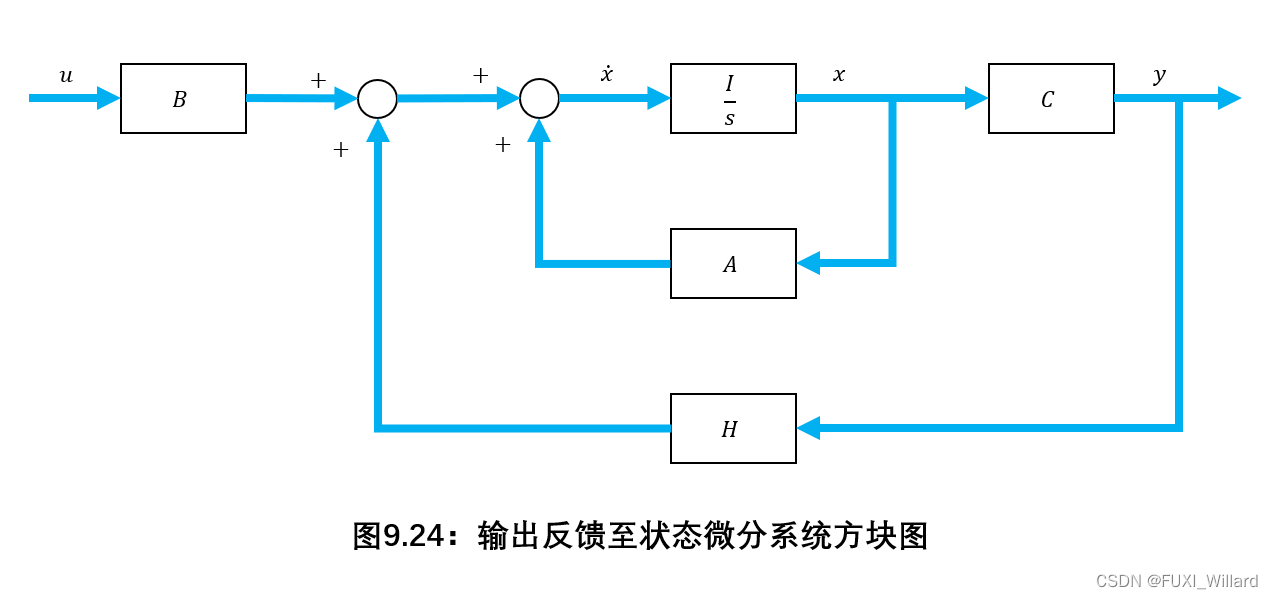
   输出反馈系统的动态方程为：
   $$\dot{x}=Ax+Bu-Hy=(A-HC)x+Bu,y=Cx$$
   其传递矩阵为：
   $$G_H(s)=C(sI-A+HC{)}^{-1}B$$
   将输出量反馈至输入系统方块图如下图所示：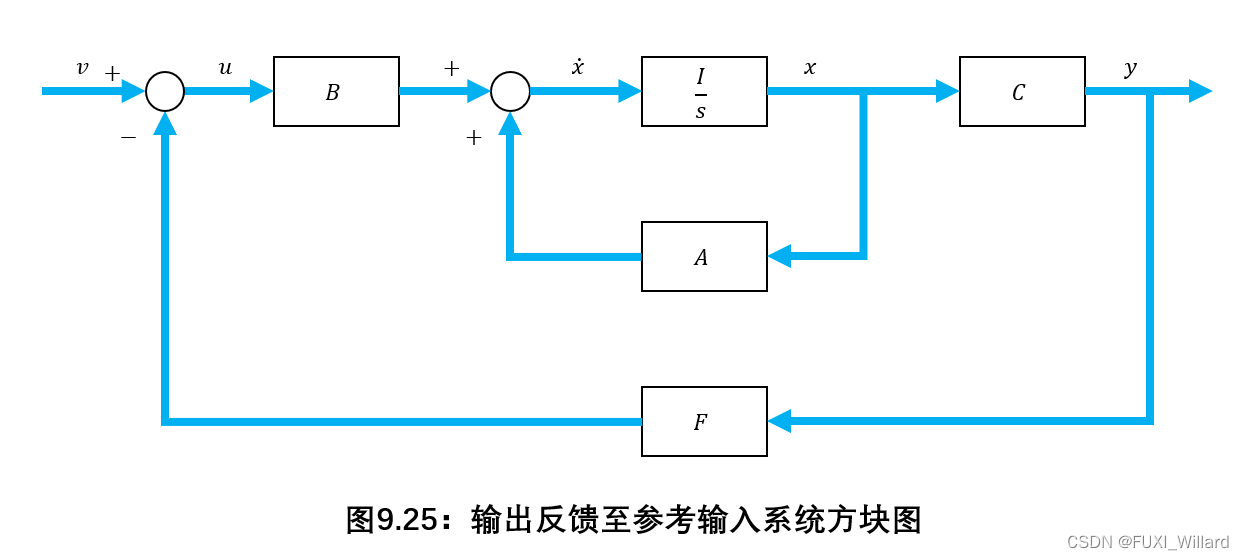

   

   当将系统的控制量$u$取为输出$y$的线性函数：
   $$u=v-Fy$$
   称为线性非动态输出反馈，简称输出反馈，其中$v$为$p$维参考输入向量，$F$为$p\times q$维实反馈增益矩阵，是一种最常用的输出反馈；

   综合整理可得输出反馈系统动态方程：
   $$\dot{x}=(A-BFC)x+Bv,y=Cx$$
   其传递函数矩阵为：
   $$G_F(s)=C(sI-A+BFC{)}^{-1}B$$
   利用状态反馈时，其信息量大而完整，可以在不增加系统维数的情况下，自由地支配响应特性；输出反馈仅利用状态变量的线性组合进行反馈，其信息量较小，所引入的补偿装置将使系统维数增加，且难以得到任意的所期望的响应特性；

3.1.2 反馈结构对系统性能的影响

1. 对系统可控性和可观测性的影响

   定理$1$：对于线性定常系统，状态反馈的引入不改变系统的可控性，但可能改变系统的可观测性；

   状态反馈可能改变系统的可观测性，其原因是状态反馈造成了所配置的极点与零点相对消；

   定理$2$：对于线性定常系统，输出至状态微分反馈的引入不改变的可观测性，但可能改变系统的可控性；

   定理$3$：对于线性定常系统，输出至参考输入反馈的引入能同时不改变系统的可控性和可观测性，即输出反馈系统${\Sigma }_F$为可控(可观测)的充分必要条件是被控系统${\Sigma }_0$为可控(可观测)；

2. 对系统稳定性的影响

   状态反馈和输出反馈都能影响系统的稳定性，加入反馈，使得通过反馈构成的闭环系统成为稳定系统，称之为镇定；

   对于线性定常被控系统：
   $$\dot{x}=Ax+Bu$$
   如果可以找到状态反馈控制律：
   $$u=-Kx+v$$
   其中：$v$为参考输入，使得通过反馈构成的闭环系统：
   $$\dot{x}=(A-BK)x+Bv$$
   是渐近稳定的，即$(A-BK)$的特征值均具有负实部，则称系统实现了状态反馈镇定；

   定理$4$：当且仅当线性定常系统的不可控部分渐近稳定时，系统是状态反馈可镇定的；

3.2 系统的极点配置

状态反馈和输出反馈都能改变闭环系统的极点位置；极点配置：利用状态反馈或输出反馈使闭环系统的极点位于所希望的极点位置；

1. 极点可配置条件

   1. 利用状态反馈的极点可配置条件

      定理$5$：利用状态反馈任意配置闭环极点的充分必要条件是被控线性定常系统可控。

   2. 利用输出反馈的极点可配置条件

      定理$6$：用输出至状态微分的反馈任意配置闭环极点的充分必要条件是被控系统(1)可观测；

2. 单输入-单输出系统的极点配置算法

   配置步骤：

   1. 列写系统状态方程及状态反馈控制律
      $$\dot{x}=Ax+bu,u=v-kx$$
      其中： k = [ k 0 k 1 ⋯ k n − 1 ] k=

      [k0k1⋯kn−1]" role="presentation" style="position: relative;">[k0k1⋯kn−1]$$\left[\begin{array}{cccc}{k}_0& k_1& \cdots & k_{n-1}\end{array}\right]$$
      k=[k0​​k1​​⋯​kn−1​​]；

   2. 检验$(A,b)$的可控性，若 r a n k [ b A b ⋯ A n − 1 b ] = n {\rm rank}

      [bAb⋯An−1b]" role="presentation" style="position: relative;">[bAb⋯An−1b]$$\left[\begin{array}{cccc}b& Ab& \cdots & A^{n-1}b\end{array}\right]$$
      =n rank[b​Ab​⋯​An−1b​]=n，则转下一步；

   3. 由要求配置的闭环极点${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$，求出希望特征多项式$a_0^{\ast }(s)=\prod _{i=1}^n(s-{\lambda }_i)$；

   4. 计算状态反馈系统的特征多项式$a_0(s)=\det [sI-A+bk]$；

   5. 比较多项式$a_0(s)$与$a_0^{\ast }(s)$，令其对应项系数相等，可确定状态反馈增益向量$k$；

   应用极点配置方法来改善系统性能需要注意的：

   • 配置极点时并非离虚轴越远越好，以免造成系统带宽过大使抗干扰性降低；
   • 状态反馈向量$k$中的元素不宜过大，否则物理实现不易；
   • 闭环零点对系统动态性能影响甚大，在规定希望配置的闭环极点时，需要充分考虑闭环零点的影响；
   • 状态反馈对系统的零点和可观测性没有影响，只有当任意配置的极点与系统零点存在对消时，状态反馈系统的零点和可观测性将会发生改变；
   • 以上几点适用于单输入-多输出或单输出系统，不适用于多输入-多输出系统；

   实例分析：

   $Example1：$ 已知单输入线性定常系统的状态方程为：
   x ˙ = [ 0 0 0 1 − 6 0 0 1 − 12 ] x + [ 1 0 0 ] u \dot{x}=

   [0001−6001−12]" role="presentation" style="position: relative;">⎡⎣⎢0100−6100−12⎤⎦⎥$$\left[\begin{array}{ccc}0& 0& 0\\ 1& -6& 0\\ 0& 1& -12\end{array}\right]$$
   x+
   [100]" role="presentation" style="position: relative;">⎡⎣⎢100⎤⎦⎥$$\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$$
   u x˙= ​010​0−61​00−12​ ​x+ ​100​ ​u
   求状态反馈向量$k$，使系统的闭环特征值为：
   $${\lambda }_1=-2,{\lambda }_2=-1+\mathrm{j},{\lambda }_3=-1-\mathrm{j}$$
   解：

   系统的可控性判别矩阵为：
   S c = [ b A b A 2 b ] = [ 1 0 0 0 1 − 6 0 0 1 ] S_c=

   [bAbA2b]" role="presentation" style="position: relative;">[bAbA2b]$$\left[\begin{array}{ccc}b& Ab& A^{2}b\end{array}\right]$$
   =
   [10001−6001]" role="presentation" style="position: relative;">⎡⎣⎢1000100−61⎤⎦⎥$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& -6\\ 0& 0& 1\end{array}\right]$$
   Sc​=[b​Ab​A2b​]= ​100​010​0−61​ ​

   $$\mathrm{rank}{S}_c=3=n$$

   故系统可控，满足极点可配置条件。

   系统的特征多项式为：

   det ⁡ ( s I − A ) = det ⁡ [ s 0 0 − 1 s + 6 0 0 − 1 s + 12 ] = s 3 + 18 s 2 + 72 s \det(sI-A)= \det

   [s00−1s+600−1s+12]" role="presentation" style="position: relative;">⎡⎣⎢s−100s+6−100s+12⎤⎦⎥$$\left[\begin{array}{ccc}s& 0& 0\\ -1& s+6& 0\\ 0& -1& s+12\end{array}\right]$$
   =s^3+18s^2+72s det(sI−A)=det ​s−10​0s+6−1​00s+12​ ​=s3+18s2+72s

   希望特征多项式为：

   $$a_0^{\ast }(s)=(s-{\lambda }_1)(s-{\lambda }_2)(s-{\lambda }_3)=(s+2)(s+1-\mathrm{j})(s+1+\mathrm{j})=s^3+4s^2+6s+4$$

   可求得：

   k ‾ = [ a 0 ∗ − a 0 a 1 ∗ − a 1 a 2 ∗ − a 2 ] = [ 4 − 66 − 14 ] \overline{k}=

   [a0∗−a0a1∗−a1a2∗−a2]" role="presentation" style="position: relative;">[a∗0−a0a∗1−a1a∗2−a2]$$\left[\begin{array}{ccc}{a}_0^{\ast }-a_0& a_1^{\ast }-a_1& a_2^{\ast }-a_2\end{array}\right]$$
   =
   [4−66−14]" role="presentation" style="position: relative;">[4−66−14]$$\left[\begin{array}{ccc}4& -66& -14\end{array}\right]$$
   k=[a0∗​−a0​​a1∗​−a1​​a2∗​−a2​​]=[4​−66​−14​]

   变换矩阵为：

   P − 1 = [ A 2 b A b b ] [ 1 0 0 a 2 1 0 a 1 a 2 1 ] = [ 1 0 0 − 6 1 0 1 0 0 ] [ 1 0 0 18 1 0 72 18 1 ] = [ 72 18 1 12 1 0 1 0 0 ] P^{-1}=

   [A2bAbb]" role="presentation" style="position: relative;">[A2bAbb]$$\left[\begin{array}{ccc}{A}^{2}b& Ab& b\end{array}\right]$$
   [100a210a1a21]" role="presentation" style="position: relative;">⎡⎣⎢1a2a101a2001⎤⎦⎥$$\left[\begin{array}{ccc}1& 0& 0\\ a_2& 1& 0\\ a_1& a_2& 1\end{array}\right]$$
   =
   [100−610100]" role="presentation" style="position: relative;">⎡⎣⎢1−61010000⎤⎦⎥$$\left[\begin{array}{ccc}1& 0& 0\\ -6& 1& 0\\ 1& 0& 0\end{array}\right]$$
   [100181072181]" role="presentation" style="position: relative;">⎡⎣⎢118720118001⎤⎦⎥$$\left[\begin{array}{ccc}1& 0& 0\\ 18& 1& 0\\ 72& 18& 1\end{array}\right]$$
   =
   [721811210100]" role="presentation" style="position: relative;">⎡⎣⎢721211810100⎤⎦⎥$$\left[\begin{array}{ccc}72& 18& 1\\ 12& 1& 0\\ 1& 0& 0\end{array}\right]$$
   P−1=[A2b​Ab​b​] ​1a2​a1​​01a2​​001​ ​= ​1−61​010​000​ ​ ​11872​0118​001​ ​= ​72121​1810​100​ ​

   P = [ 0 0 1 0 1 − 12 1 − 18 144 ] P=

   [00101−121−18144]" role="presentation" style="position: relative;">⎡⎣⎢00101−181−12144⎤⎦⎥$$\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& -12\\ 1& -18& 144\end{array}\right]$$
   P= ​001​01−18​1−12144​ ​

   k = k ‾ P = [ 4 − 66 − 14 ] [ 0 0 1 0 1 − 12 1 − 18 144 ] = [ − 14 186 − 1220 ] k=\overline{k}P=

   [4−66−14]" role="presentation" style="position: relative;">[4−66−14]$$\left[\begin{array}{ccc}4& -66& -14\end{array}\right]$$
   [00101−121−18144]" role="presentation" style="position: relative;">⎡⎣⎢00101−181−12144⎤⎦⎥$$\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& -12\\ 1& -18& 144\end{array}\right]$$
   =
   [−14186−1220]" role="presentation" style="position: relative;">[−14186−1220]$$\left[\begin{array}{ccc}-14& 186& -1220\end{array}\right]$$
   k=kP=[4​−66​−14​] ​001​01−18​1−12144​ ​=[−14​186​−1220​]

   或
   a 0 ∗ ( s ) = det ⁡ ( s I − A + b k ) = [ s + k 1 k 2 k 3 − 1 s + 6 0 0 − 1 s + 12 ] = s 3 + ( k 1 + 18 ) s 2 + ( 18 k 1 + k 2 + 72 ) s + ( 72 k 1 + 12 k 2 + k 3 )

   a0∗(s)=det(sI−A+bk)=[s+k1k2k3−1s+600−1s+12]=s3+(k1+18)s2+(18k1+k2+72)s+(72k1+12k2+k3)" role="presentation" style="position: relative;">a∗0(s)=det(sI−A+bk)=⎡⎣⎢s+k1−10k2s+6−1k30s+12⎤⎦⎥=s3+(k1+18)s2+(18k1+k2+72)s+(72k1+12k2+k3)$$\begin{array}{rl}{a}_0^{\ast }(s)& =det(sI-A+bk)\\ & =\left[\begin{array}{ccc}s+k_1& k_2& k_3\\ -1& s+6& 0\\ 0& -1& s+12\end{array}\right]\\ & =s^3+(k_1+18)s^2+(18k_1+k_2+72)s+(72k_1+12k_2+k_3)\end{array}$$
   a0∗​(s)​=det(sI−A+bk)= ​s+k1​−10​k2​s+6−1​k3​0s+12​ ​=s3+(k1​+18)s2+(18k1​+k2​+72)s+(72k1​+12k2​+k3​)​

   { k 1 + 18 = 4 18 k 1 + k 2 + 72 = 6 72 k 1 + 12 k 2 + k 3 = 4

   {k1+18=418k1+k2+72=672k1+12k2+k3=4" role="presentation" style="position: relative;">⎧⎩⎨k1+18=418k1+k2+72=672k1+12k2+k3=4$$\{\begin{array}{ll}& k_1+18=4\\ & 18k_1+k_2+72=6\\ & 72k_1+12k_2+k_3=4\end{array}$$
   ⎩ ⎨ ⎧​​k1​+18=418k1​+k2​+72=672k1​+12k2​+k3​=4​

   求得：
   $$k_1=-14,k_2=186,k_3=-1220$$
   可得：
   k = [ k 1 k 2 k 3 ] = [ − 14 186 − 1220 ] k=

   [k1k2k3]" role="presentation" style="position: relative;">[k1k2k3]$$\left[\begin{array}{ccc}{k}_1& k_2& k_3\end{array}\right]$$
   =
   [−14186−1220]" role="presentation" style="position: relative;">[−14186−1220]$$\left[\begin{array}{ccc}-14& 186& -1220\end{array}\right]$$
   k=[k1​​k2​​k3​​]=[−14​186​−1220​]

3. 状态反馈对传递函数零点的影响

   状态反馈对$G(s)$的零点没有影响，仅使$G(s)$的极点改变为闭环系统极点，但可能引入状态反馈后恰巧使某些极点移到$G(s)$的零点处而构成极、零点对消，这时既失去了一个系统零点，又失去了一个系统极点，且被对消掉的那些极点可能不可观测；

3.3 全维状态观测器及其设计

很多情况下，多数状态变量不易测得或不可能测得，可利用被控对象的输入量和输出量建立状态观测器(亦称状态估计器、状态重构器)来重构状态的问题，当重构状态向量的维数等于被控对象状态向量的维数时，称为全维状态观测器；

1. 全维状态观测器构成方案

   设被控对象动态方程为：
   $$\dot{x}=Ax+Bu,y=Cx$$
   构造一个动态方程与上式相同且能用计算机实现的模拟被控系统：
   $$\dot{\hat{x}}=A\hat{x}+Bu,\hat{y}=C\hat{x}$$
   式中：$\hat{x}、\hat{y}$分别为模拟系统的状态向量和输出向量，是被控对象状态向量和输出向量的估值；

   

   状态观测器有两个输入，即$u$和$y$，输出为$\hat{x}$，观测器含$n$个积分器并对全部状态变量做出估计；$H$为观测器输出反馈阵，把$(\hat{y}-y)$负反馈至$\dot{\hat{x}}$处，是为配置观测器极点，提高其动态性能，即尽快使$(\hat{x}-x)$逼近于零而引入的；

2. 全维状态观测器分析设计

   由上图可列出全维状态观测器动态方程：
   $$\dot{\hat{x}}=A\hat{x}+Bu-H(\hat{y}-y),\hat{y}=C\hat{x}$$
   故有：
   $$\dot{\hat{x}}=A\hat{x}+Bu-HC(\hat{x}-x)=(A-HC)\hat{x}+Bu+Hy$$
   式中：$(A-HC)$称为观测器系统矩阵；

   观测器分析设计的关键问题是能否在任何初始条件下，即尽管$\hat{x}(t_0)$与与$x(t_0)$不同，但总能保证下式成立：
   $$\underset{t\to \infty }{\lim }(\hat{x}(t)-x(t))=0$$
   只有满足上式，状态反馈系统才能正常工作，称为观测器存在条件；

   定理$7$：若被控系统$(A,B,C)$可观测，则其状态可用形如
   $$\dot{\hat{x}}=A\hat{x}+Bu-HC(\hat{x}-x)=(A-HC)\hat{x}+Bu+Hy$$
   的全维状态观测器给出估值，其中矩阵$H$按任意配置观测器极点的需要来选择，以决定状态误差衰减的速率；

   实例分析：

   $Example2：$ 设被控对象传递函数为：
   $$\frac{Y(s)}{U(s)}=\frac{2}{(s+1)(s+2)}$$
   设计全维状态观测器，将极点配置在$-10,-10$。

   解：

   被控对象的传递函数为：
   $$\frac{Y(s)}{U(s)}=\frac{2}{(s+1)(s+2)}=\frac{2}{s^2+3s+2}$$
   根据传递函数直接写出系统的可控标准型：
   $$\dot{x}=Ax+bu,y=cx$$
   其中：
   A = [ 0 1 − 2 − 3 ] , b = [ 0 1 ] , c = [ 2 0 ] A=

   [01−2−3]" role="presentation" style="position: relative;">[0−21−3]$$\left[\begin{array}{cc}0& 1\\ -2& -3\end{array}\right]$$
   ,b=
   [01]" role="presentation" style="position: relative;">[01]$$\left[\begin{array}{c}0\\ 1\end{array}\right]$$
   ,c=
   [20]" role="presentation" style="position: relative;">[20]$$\left[\begin{array}{cc}2& 0\end{array}\right]$$
   A=[0−2​1−3​],b=[01​],c=[2​0​]
   系统可控可观测，$n=2,q=1$，输出反馈向量$h$为$2\times 1$向量.

   全维状态观测器系统矩阵为：
   A − h c = [ 0 1 − 2 − 3 ] − [ h 0 h 1 ] [ 2 0 ] = [ − 2 h 0 1 − 2 − 2 h 1 − 3 ] A-hc=

   [01−2−3]" role="presentation" style="position: relative;">[0−21−3]$$\left[\begin{array}{cc}0& 1\\ -2& -3\end{array}\right]$$
   -
   [h0h1]" role="presentation" style="position: relative;">[h0h1]$$\left[\begin{array}{c}{h}_0\\ h_1\end{array}\right]$$
   [20]" role="presentation" style="position: relative;">[20]$$\left[\begin{array}{cc}2& 0\end{array}\right]$$
   =
   [−2h01−2−2h1−3]" role="presentation" style="position: relative;">[−2h0−2−2h11−3]$$\left[\begin{array}{cc}-2h_0& 1\\ -2-2h_1& -3\end{array}\right]$$
   A−hc=[0−2​1−3​]−[h0​h1​​][2​0​]=[−2h0​−2−2h1​​1−3​]
   观测器特征方程为：
   $$|\lambda I-(A-hc)|={\lambda }^2+(2h_0+3)\lambda +(6h_0+2h_1+2)=0$$
   期望特征方程为：
   $$(\lambda +10{)}^2={\lambda }^2+20\lambda +100=0$$
   令两特征方程同次项系数相等，可得：
   $$2h_0+3=20,6h_0+2h_1+2=100$$
   解得：
   $$h_0=8.5,h_1=23.5$$
   其中：$h_0,h_1$分别为$(\hat{y}-y)$引至${\dot{\hat{x}}}_1,{\dot{\hat{x}}}_2$的反馈系数；

   被控对象及全维状态观测器组合系统的状态变量图如下图所示：

   

3. 分离特性

   定理$8$(分离定理)：若被控系统$(A,B,C)$可控可观测，用状态观测器估值形成状态反馈时，其系统的极点配置和观测器设计可分别独立进行，即$K$和$H$阵的设计可分别独立进行；