-
动态开点线段树(C++实现)
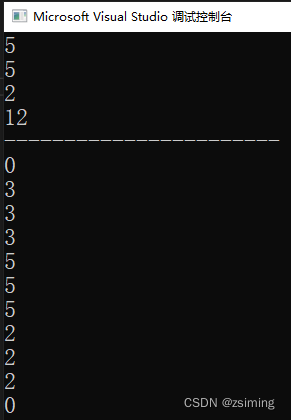
09-17更新:针对评论区的错误,原来是在推懒标记的时候需要 += 而不是 =。提供了更新后的测试:
int main() { SegTree st; st.upDate(st.root_, 0, 1e9, 5, 10, 2); st.upDate(st.root_, 0, 1e9, 2, 7, 3); cout << st.query(st.root_, 0, 1e9, 6, 6) << endl; cout << st.query(st.root_, 0, 1e9, 7, 7) << endl; cout << st.query(st.root_, 0, 1e9, 8, 8) << endl; cout << st.query(st.root_, 0, 1e9, 6, 8) << endl; cout << "-----------------------" << endl; cout << st.query(st.root_, 0, 1e9, 1, 1) << endl; cout << st.query(st.root_, 0, 1e9, 2, 2) << endl; cout << st.query(st.root_, 0, 1e9, 3, 3) << endl; cout << st.query(st.root_, 0, 1e9, 4, 4) << endl; cout << st.query(st.root_, 0, 1e9, 5, 5) << endl; cout << st.query(st.root_, 0, 1e9, 6, 6) << endl; cout << st.query(st.root_, 0, 1e9, 7, 7) << endl; cout << st.query(st.root_, 0, 1e9, 8, 8) << endl; cout << st.query(st.root_, 0, 1e9, 9, 9) << endl; cout << st.query(st.root_, 0, 1e9, 10, 10) << endl; cout << st.query(st.root_, 0, 1e9, 11, 11) << endl; return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
结果:
1. 问题背景
线段树主要是针对区间问题而生的一种数据结构。当频繁的对某个区间的元素(或者某个元素)进行加减后,再求某个区间的和就可以使用线段树来实现快速的查询。
在实现上,线段树一般使用二叉树来实现(即使是使用数组,也是模拟了完全二叉树)。假设我现在有数组如下:
nums=[3,5,1,1,2]。那么,根据这个数组可以拆分的区间,可以构造如下的二叉树:
每个结点都是维护了一个区间的性质(在上图里面表示一个区间的和),区间的最小长度为1,也就是这个区间有且仅有一个元素。首先,我们先简单的看看这棵树是怎么工作的,然后再去实现这颗树。假设我要查询区间
[2,4]之间的元素之和,那么这颗树要怎么计算这个和呢?结果就是只用到了下图的红色结点:

正常来看的话,计算
[2,4]区间的值可能会使用[2,2],[3,3],[4,4],但是对于[3,3],[4,4]来说,只需要访问它们的父节点就可以知道区间的和是多少了,因此访问两个孩子结点的过程变成了访问一次父亲结点。这样,在数据比较多,查询的区间比较长的时候,能极大的加快查询的速度,把区间
O(n)的时间复杂度变成logn的时间复杂度。下面主要讲怎么去实现这颗线段树,以及接口的封装。
2. 代码实现
首先,很多解法里面都是使用数组来实现线段树,但是这样的坏处就是需要提前开很大的空间(一般是
4 * 数组长度),在这里,我们使用二叉树的方式进行实现。且对于一些没用到结点是不会创建的,由此称为动态开点。首先实现树结点这个数据结构:
struct Node { Node () : left_(nullptr), right_(nullptr), val_(0), lazy_(0) {} int val_; int lazy_; Node* left_; Node* right_; };- 1
- 2
- 3
- 4
- 5
- 6
- 7
(
Tips:在讲到懒标记之前,我们先忽略所有跟lazy相关的变量和语句)对于线段树,最核心的功能就是修改区间(给某个区间加上/减去一个数)和区间查询。我们首先考虑区间修改的接口:
// 更新区间值 void upDate(Node* curNode, int curLeft, int curRight, int upDateLeft, int upDateRight, int addVal) { if (upDateLeft <= curLeft && upDateRight >= curRight) { // 如果需要更新的区间[upDateLeft, upDateRight] 包含了 当前这个区间[curLeft, curRight] // 那么暂存一下更新的值 // 等到什么时候用到孩子结点了,再把更新的值发放给孩子 curNode->val_ += addVal * (curRight - curLeft + 1); curNode->lazy_ += addVal; return; } // 到这里说明要用到左右孩子了 // 因此,要用pushDown函数把懒标签的值传递下去 int mid = (curLeft + curRight) / 2; pushDown(curNode, mid - curLeft + 1, curRight - mid); // 说明在[curLeft, curRight]中, if (upDateLeft <= mid) { upDate(curNode->left_, curLeft, mid, upDateLeft, upDateRight, addVal); } if (upDateRight > mid) { upDate(curNode->right_, mid + 1, curRight, upDateLeft, upDateRight, addVal); } // 更新了子节点还需要更新现在的结点 pushUp(curNode); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
我们看一下这段代码做了什么。
对于
upDate这个接口的形参,curNode是当前结点,curLeft是当前结点所表示的左边界,curRight是当前结点表示的右边界。而upDateLeft 和 updateRight则表示是需要对区间[upDateLeft,updateRight]里面每个元素都加上addVal。首先,当需改修改的区间包含了当前的区间,那么我们更新了当前结点的值,然后马上返回了。而不能覆盖的话,我们需要往左右孩子表示的区间去更新,为什么呢?我们再拿前面的例子说明:

对于上面的例子,要为[2,4]区间内的每个元素增加1,那么首先看区间[0,4]。区间[2,4]根本包不住区间[0,4],那么只能往左右孩子看。对于左孩子[0,2],[2,4]也包不住[0,2],因此只能再去看区间[2,2]。结果[2,4]能包住区间[2,2],所以在这儿就停止了返回了。而[2,4]能包住[3,4],因此在[3,4]也停止并返回了。上面的代码,刚好包含了
包得住马上返回、包不住找左孩子、包不住找右孩子的情况(3个if语句)。我们主要到还有pushDown 和 pushUp的操作。我们先看代码:
// 把结点curNode的懒标记分发给左右孩子 然后自己的懒标记清零 void pushDown(Node* curNode, int leftChildNum, int rightChildNum) { if (curNode->left_ == nullptr) curNode->left_ = new Node; if (curNode->right_ == nullptr) curNode->right_ = new Node; if (curNode->lazy_ == 0) return; curNode->left_->val_ += curNode->lazy_ * leftChildNum; curNode->left_->lazy_ += curNode->lazy_; // 09-17更正 = ----> += curNode->right_->val_ += curNode->lazy_ * rightChildNum; curNode->right_->lazy_ += curNode->lazy_; // 09-17更正 = ----> += curNode->lazy_ = 0; // 注意不需要递归再继续下推懒标签 // 每次只需要推一层即可 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
// 一般是子节点因为要被用到了,所以需要更新值 因此也要同时更新父节点的值 void pushUp(Node* curNode) { curNode->val_ = curNode->left_->val_ + curNode->right_->val_; }- 1
- 2
- 3
- 4
对于
pushDown这个操作其实是和懒标记息息相关的。所谓懒标记,就是把本区间一些增加的量给保留下来,等到需要用到左右结点的时候,才把这些增加的量分给左右孩子,让它们去更新自己区间的值。这样,多次增加的操作就可以变成一次,大大增加效率。所以,对于pushDown这个函数来说就是把之前在结点curNode上拦截下来的量分给左右孩子,让他们去更新区间的值。- 问:为什么需要用到左右孩子就需要
pushDown? - 答:因为不
pushDown的话,左右孩子的值都是没更新的。 - 问:为啥没更新?
- 答:因为如果能拦截的话,那么计算只用到了它们的父节点,只需要更新父节点就行了(第一个
if语句括号内做的事情),所以子节点更不更新根本无所谓。但是现在要用到左右孩子了,必须更新了,因此要用pushDown这个操作把孩子结点的值更新为正确的值。
我们还注意到,有个
pushUp的操作。这个操作基本是和pushDown成对出现的。因为左右孩子的值更新了,所以本结点的值也要更新。pushUp做的就是这件事。另一个重要的接口就是查询:
// 查询 int query(Node* curNode, int curLeft, int curRight, int queryLeft, int queryRight) { if (queryLeft <= curLeft && queryRight >= curRight) { return curNode->val_; } // 用到左右结点力 先下推! int mid = (curLeft + curRight) / 2; pushDown(curNode, mid - curLeft + 1, curRight - mid); int curSum = 0; if (queryLeft <= mid) curSum += query(curNode->left_, curLeft, mid, queryLeft, queryRight); if (queryRight > mid) curSum += query(curNode->right_, mid + 1, curRight, queryLeft, queryRight); return curSum; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
在这个代码中,第一个
if语句表示的就是拦截动作,直接返回本结点的结果:

而不能拦截的,则去左右孩子看一下能不能拦截(第2、3个if语句)。至此,代码基本完成。
完整代码:
class SegTree { private: struct Node { Node () : left_(nullptr), right_(nullptr), val_(0), lazy_(0) {} int val_; int lazy_; Node* left_; Node* right_; }; public: Node* root_; SegTree() { root_ = new Node(); } ~SegTree() {} // 更新区间值 void upDate(Node* curNode, int curLeft, int curRight, int upDateLeft, int upDateRight, int addVal) { if (upDateLeft <= curLeft && upDateRight >= curRight) { // 如果需要更新的区间[upDateLeft, upDateRight] 包含了 当前这个区间[curLeft, curRight] // 那么暂存一下更新的值 // 等到什么时候用到孩子结点了,再把更新的值发放给孩子 curNode->val_ += addVal * (curRight - curLeft + 1); curNode->lazy_ += addVal; return; } // 到这里说明要用到左右孩子了 // 因此,要用pushDown函数把懒标签的值传递下去 int mid = (curLeft + curRight) / 2; pushDown(curNode, mid - curLeft + 1, curRight - mid); // 说明在[curLeft, curRight]中, if (upDateLeft <= mid) { upDate(curNode->left_, curLeft, mid, upDateLeft, upDateRight, addVal); } if (upDateRight > mid) { upDate(curNode->right_, mid + 1, curRight, upDateLeft, upDateRight, addVal); } // 更新了子节点还需要更新现在的结点 pushUp(curNode); } // 把结点curNode的懒标记分发给左右孩子 然后自己的懒标记清零 void pushDown(Node* curNode, int leftChildNum, int rightChildNum) { if (curNode->left_ == nullptr) curNode->left_ = new Node; if (curNode->right_ == nullptr) curNode->right_ = new Node; if (curNode->lazy_ == 0) return; curNode->left_->val_ += curNode->lazy_ * leftChildNum; curNode->left_->lazy_ += curNode->lazy_; curNode->right_->val_ += curNode->lazy_ * rightChildNum; curNode->right_->lazy_ += curNode->lazy_; curNode->lazy_ = 0; // 注意不需要递归再继续下推懒标签 // 每次只需要推一层即可 } // 一般是子节点因为要被用到了,所以需要更新值 因此也要同时更新父节点的值 void pushUp(Node* curNode) { curNode->val_ = curNode->left_->val_ + curNode->right_->val_; } // 查询 int query(Node* curNode, int curLeft, int curRight, int queryLeft, int queryRight) { if (queryLeft <= curLeft && queryRight >= curRight) { return curNode->val_; } // 用到左右结点力 先下推! int mid = (curLeft + curRight) / 2; pushDown(curNode, mid - curLeft + 1, curRight - mid); int curSum = 0; if (queryLeft <= mid) curSum += query(curNode->left_, curLeft, mid, queryLeft, queryRight); if (queryRight > mid) curSum += query(curNode->right_, mid + 1, curRight, queryLeft, queryRight); return curSum; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
实战:
Leetcode729:

很明显,这道题就是在制定某个形成区间前,查一下这个区间是不是有安排了(有的话这个区间的和大于1,没有的话等于0,每次制定一个行程区间都是为这个区间的所有元素+1)。题解:
class MyCalendar { public: MyCalendar() { root_ = new Node(); } ~MyCalendar() { delete root_; } private: struct Node { Node () : left_(nullptr), right_(nullptr), val_(0), lazy_(0) {} int val_; int lazy_; Node* left_; Node* right_; }; public: Node* root_; // 更新区间值 void upDate(Node* curNode, int curLeft, int curRight, int upDateLeft, int upDateRight, int addVal) { if (upDateLeft <= curLeft && upDateRight >= curRight) { // 如果需要更新的区间[upDateLeft, upDateRight] 包含了 当前这个区间[curLeft, curRight] // 那么暂存一下更新的值 // 等到什么时候用到孩子结点了,再把更新的值发放给孩子 curNode->val_ += addVal * (curRight - curLeft + 1); curNode->lazy_ += addVal; return; } // 到这里说明要用到左右孩子了 // 因此,要用pushDown函数把懒标签的值传递下去 int mid = (curLeft + curRight) / 2; pushDown(curNode, mid - curLeft + 1, curRight - mid); // 说明在[curLeft, curRight]中, if (upDateLeft <= mid) { upDate(curNode->left_, curLeft, mid, upDateLeft, upDateRight, addVal); } if (upDateRight > mid) { upDate(curNode->right_, mid + 1, curRight, upDateLeft, upDateRight, addVal); } // 更新了子节点还需要更新现在的结点 pushUp(curNode); } // 把结点curNode的懒标记分发给左右孩子 然后自己的懒标记清零 void pushDown(Node* curNode, int leftChildNum, int rightChildNum) { if (curNode->left_ == nullptr) curNode->left_ = new Node; if (curNode->right_ == nullptr) curNode->right_ = new Node; curNode->left_->val_ += curNode->lazy_ * leftChildNum; curNode->left_->lazy_ = curNode->lazy_; curNode->right_->val_ += curNode->lazy_ * rightChildNum; curNode->right_->lazy_ = curNode->lazy_; // 注意不需要递归再继续下推懒标签 // 每次只需要推一层即可 } // 一般是子节点因为要被用到了,所以需要更新值 因此也要同时更新父节点的值 void pushUp(Node* curNode) { curNode->val_ = curNode->left_->val_ + curNode->right_->val_; } // 查询 int query(Node* curNode, int curLeft, int curRight, int queryLeft, int queryRight) { if (queryLeft <= curLeft && queryRight >= curRight) { return curNode->val_; } // 用到左右结点力 先下推! int mid = (curLeft + curRight) / 2; pushDown(curNode, mid - curLeft + 1, curRight - mid); int curSum = 0; if (queryLeft <= mid) curSum += query(curNode->left_, curLeft, mid, queryLeft, queryRight); if (queryRight > mid) curSum += query(curNode->right_, mid + 1, curRight, queryLeft, queryRight); return curSum; } bool book(int start, int end) { if (query(root_, 0, 1e9, start, end)) return false; upDate(root_, 0, 1e9, start, end, 1); return true; } }; /** * Your MyCalendar object will be instantiated and called as such: * MyCalendar* obj = new MyCalendar(); * bool param_1 = obj->book(start,end); */- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
-
相关阅读:
Linux---su:鉴定故障
Echarts——vue+echarts 简单使用折线图
联合投稿其乐融融 抖音共创助你大显身手
【必知必会的MySQL知识】④DCL语言
29. 一道简单背包题
【云原生 • Kubernetes】k8s功能特性、k8s集群架构介绍
云原生正在吞噬一切,开发者该如何应对?
word行距怎么设置?专业排版,让文档更具吸引力!
简单理解AIGC大模型
springboot+jsp+bootstrap+java问卷调查系统
- 原文地址:https://blog.csdn.net/zsiming/article/details/126799018
