赫夫曼树、赫夫曼编码

基本介绍

给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度(wpl)达到最小，称这样的二叉树为最优二叉树，也称为赫夫曼树(HuffmanTree)。
赫夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

重要概念

1. 路径和路径长度:
   在一棵树中，从一个结点往下可以达到的孩子节点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1
2. 结点的权及带权路径长度:
   若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积
3. 树的带权路径长度:
   树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL(weighted path length),权值越大的结点离根结点越近的二叉树才是最优二叉树。
4. WPL最小的就是赫夫曼树
   

赫夫曼树创建

例如：一个数组 arr={13,7,8,3,29,6,1};
排序后
arr={1,3,6,7,8,13,29};







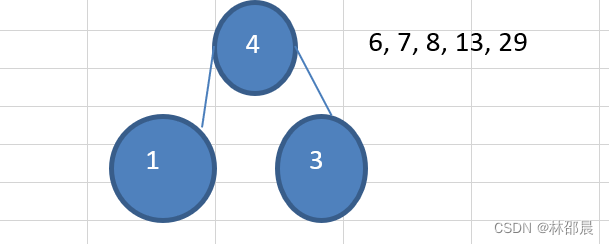
代码实现：

package HuffmanTree;

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

/**
 * 创建赫夫曼树
 * @author 86178
 *
 */
public class HuffmanTreeDemo {
	public static void main(String[] args) {
		int[] arr= {7,6,8,29,13,1,3};
		Node root=createTree(arr);
		pre(root);
	}
	//创建赫夫曼树
	public static Node createTree(int[] arr) {
		List<Node> list=new ArrayList<>();
		for(int v:arr) {
			list.add(new Node(v));
		}
		//list最终只剩root根结点
		while (list.size()>1) {
			Collections.sort(list);//排序
			Node left=list.get(0); //取出最小结点
			Node right=list.get(1); //取出次小结点
			Node parent=new Node(left.value+right.value);//新建父结点
			parent.left=left;//建立左节点关系
			parent.right=right;//建立右节点关系
			list.remove(left);//删除
			list.remove(right);//删除
			list.add(parent);//将父结点添加进list
		}
		return list.get(0);//返回root
	}
	//先序遍历打印结点信息
	public static void pre(Node head) {
		System.out.println(head);
		if (head.left!=null) {
			pre(head.left);
		}
		if (head.right!=null) {
			pre(head.right);
		}
	}
}
//实现Comparable接口，便于排序
class Node implements Comparable<Node> {
	int value;
	Node left;
	Node right;
	
	public Node(int v) {
		this.value=v;
	}
	
	public String toString() {
		return "[Node="+this.value+"]";
	}
	@Override
	public int compareTo(Node o) {
		return this.value-o.value;
	}
	
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

赫夫曼编码

• 赫夫曼编码也翻译为哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式,属于一种程序算法。
• 赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。
• 赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在20%～90%之间。
• 赫夫曼码是可变字长编码(VLC)的一种。Huffman于1952年提出种编码方法，称之为最佳编码。

定长编码

• 例如: 一个字符串，s=“i like java”;共有11个字符，包括空格
• 对应ASCII码值为 105 32 108 105 107 101 32 106 97 118 97
• 进一步转换为二进制为 01101001 00100000 01101110 01101001 01101011 01100101
  00100000 01101010 01100001 01110110 01100001
• 最终按照二进制传递信息，总长度为98，包括空格。

变长编码

• 例如: 一个字符串，s=“i like like like java do you like a java”;共有40个字符，包括空格
• 统计各个字符出现的个数 d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9
• 对应编码： 0=，1=a,10=i, 11=e,100=k,101=l,110=o,111=v,1000=j, 1001=u,1010=y, 1011=d
• 说明:按照各个字符出现的次数进行编码，原则是出现次数越多的，则编码越小，比如 空格出现了9次，编码为0,其它依次类推.
• 按照上面给各个字符规定的编码，则我们在传输“i like like like java do you like a
  java"数据时，编码就是10010110100…
• 字符的编码都不能是其他字符编码的前缀，符合此要求的编码叫做前缀编码，即不能匹配到重复的编码。

赫夫曼编码

• 例如: 一个字符串，s=“i like like like java do you like a java”;共有40个字符，包括空格
• 统计各个字符出现的个数 d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9
• 构建赫夫曼树
  
• 根据赫夫曼树，给各个字符规定编码，向左的路径为0，向右的路径为1。
• 编码如下: o: 1000 u: 10010 d:100110 y: 100111 i: 101a : 110k: 1110e: 1111j: 0000v: 0001l: 001 : 01
• 按照上面的赫夫曼编码，我们的"i like like like javado you like a java"字符串对应的编码为(注意这里我们使用的无损压缩)
  1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110
  长度为:133
• 说明:原来长度是359,压缩了(359-133)/ 359= 62.9%2)此编码满足前缀编码,即字符的编码都不能是其 他字符编码的前缀。不会造成匹配的多义性。

注意，这个赫夫曼树根据排序方法不同（有多个相等的值），也可能不太一样，这样对应的赫夫曼编码也不完全一样，但是wpl是一样的，都是最小的。