手动构造感知机模型Perceptron（Numpy代码手写）

引言

首先我们要知道什么是感知机模型：

感知机的定义

感知机：
假设输入空间（特征空间）是$\chi \subseteq {\mathbb{R}}^n$，输出空间是 Y ∈ { + 1 , − 1 } Y\in\{+1,-1\} Y∈{+1,−1}。输入$x\in \chi$表示实例的特征向量，对应于输入空间（特征空间）的点；输出$y\in Y$表示实例的类别。由输入空间到输出空间的如下函数：
$f(x)=sign(\omega \cdot x+b)$
称为感知机。其中，$\omega$和$b$为感知机模型参数，$\omega \in {\mathbb{R}}^n$叫做权值或者权值向量，$b\in \mathbb{R}$叫做偏置，$\omega \cdot x$表示$\omega$和$b$的内积。$sign$是符号函数，即：
如果$x\ge 0$，$sign(x)=+1$;
如果$x<0$，$sign(x)=-1$。

感知机学习算法的原始形式

输入：训练数据集$T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$，其中$x_i\in \chi ={\mathbb{R}}^n$， y i ∈ Y = { − 1 , + 1 }    ,    i = 1 , 2 , ⋯   , N y_i\in Y=\{-1,+1\}\;,\;i=1,2,\cdots,N yi​∈Y={−1,+1},i=1,2,⋯,N，学习率$\eta (0<\eta \le 1)$；

输出：$\omega ,b$；感知机模型$f(x)=sign(\omega \cdot x+b)$

(1)选取初值${\omega }_0,b_0$；

(2)在训练数据集中选取数据$(x_i,y_i)$；

(3)如果$y_i(\omega \cdot x_i+b)\le 0$，
$$\omega \leftarrow \omega +\eta y_i{x}_i$$
$$b\leftarrow b+\eta y_i$$
(4)转至（2），直到训练集中没有误分类点。

这种算法直观上有如下解释：当一个实例点被误分类，即位于分离超平面错误一侧时，则调整$\omega ,b$的值，使得分离超平面向该误分类点的一侧移动，以减少该误分类点与超平面间的距离，直至超平面越过该误分类点使其被正确分类。

代码实现

我们使用sklearn的数据集来实现算法。

导入需要的包：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
1
2
3
4

iris=load_iris()
iris_data=iris.data
iris_dataset=pd.DataFrame(iris_data,columns=iris.feature_names)
iris_dataset['labels']=iris.target
print(iris_dataset)
1
2
3
4
5

我们看一下数据集长什么样子：

     sepal length (cm)  sepal width (cm)  ...  petal width (cm)  labels
0                  5.1               3.5  ...               0.2       0
1                  4.9               3.0  ...               0.2       0
2                  4.7               3.2  ...               0.2       0
3                  4.6               3.1  ...               0.2       0
4                  5.0               3.6  ...               0.2       0
..                 ...               ...  ...               ...     ...
145                6.7               3.0  ...               2.3       2
146                6.3               2.5  ...               1.9       2
147                6.5               3.0  ...               2.0       2
148                6.2               3.4  ...               2.3       2
149                5.9               3.0  ...               1.8       2

[150 rows x 5 columns]
1
2
3
4
5
6
7
8
9
10
11
12
13
14

我们看看每个标签值对应的数量为多少：

print(iris_dataset.labels.value_counts())
1

输出为：

0    50
1    50
2    50
Name: labels, dtype: int64
1
2
3
4

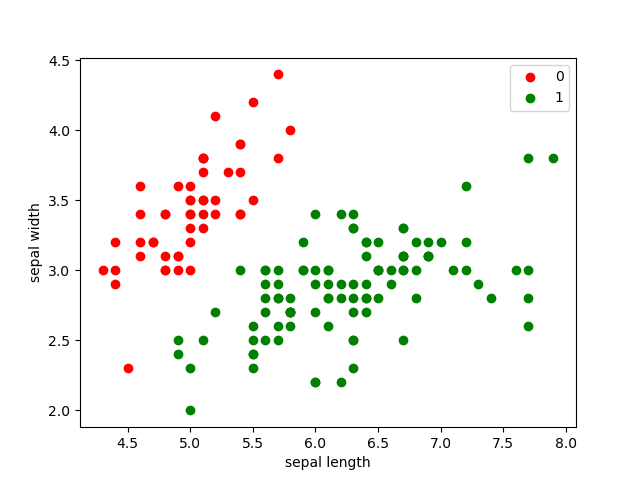
这里我们研究前两个特征，绘制出散点图：

plt.scatter(iris_dataset[:50]['sepal length (cm)'],iris_dataset[:50]['sepal width (cm)'],c='red',label='0')
plt.scatter(iris_dataset[50:]['sepal length (cm)'],iris_dataset[50:]['sepal width (cm)'],c='green',label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()
1
2
3
4
5
6

我们简单设置训练集，并对标签值做出变换：

data = np.array(iris_dataset.iloc[:100, [0, 1, -1]])
X, y = data[:,:-1], data[:,-1]
y = np.array([1 if i == 1 else -1 for i in y])
print(X.shape, y.shape)
1
2
3
4

(100, 2) (100,)
1

我们接下来定义一下感知机模型：

class Percentation:
    def __init__(self):
        pass

    def sign(self,w,x,b):
        return np.dot(w,x)+b

    def initilize_with_zeros(self,dim):
        w=np.zeros(dim,dtype=np.float32)
        b=0
        return w,b

    def train(self,X_train,y_train,learing_rate):
        w,b=self.initilize_with_zeros(X_train.shape[1])
        wrong_classify=False
        while not wrong_classify:
            wrong_classify_count=0
            for i in range(len(X_train)):
                X=X_train[i]
                y=y_train[i]
                if y*self.sign(w,X,b)<=0:
                    w+=learing_rate*np.dot(y,X)
                    b+=learing_rate*y
                    wrong_classify_count+=1
            if wrong_classify_count==0:
                wrong_classify=True
                print('there is no wrong classify')

        params={'w:':w,'b:':b}
        return params
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

我们看一下最终的结果：

parame=Percentation()
parames=parame.train(X,y,learing_rate=0.01)
print(parames)
1
2
3

输出结果为：

there is no wrong classify
{'w:': array([ 0.7879957, -1.0069965], dtype=float32), 'b:': -1.2300000000000009}
1
2

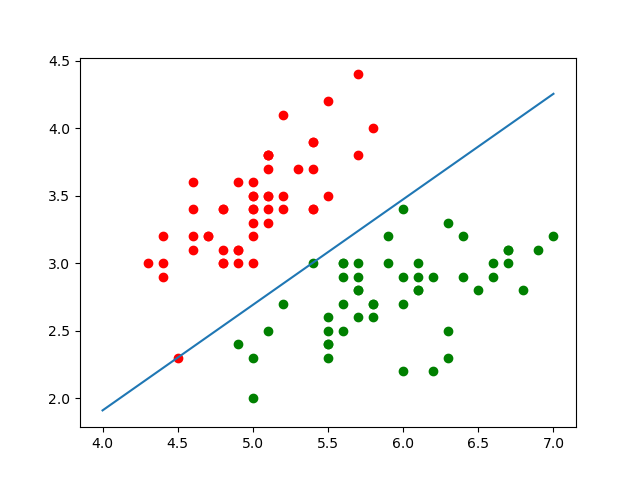
我们看一下分离超平面：

x_points=np.linspace(4,7,10)
y_hat=-(parames['w:'][0]*x_points+parames['b:'])/parames['w:'][1]
plt.plot(x_points,y_hat)
plt.scatter(data[:50, 0], data[:50, 1], color='red', label='0')
plt.scatter(data[50:100, 0], data[50:100, 1], color='green', label='1')
plt.show()
1
2
3
4
5
6