Python数据分析和挖掘之入门理论+实操

因为是赛前突击，我只选取用到的知识，后续补充

1、集中趋势、离中趋势

• 集中趋势（数据聚拢位置的一种衡量）：均值、中位数、分位数、众数
  • 四分位数计算方法
    Q1的位置：（n+1）* 0.25
    Q2的位置：（n+1）* 0.5
    Q3的位置：（n+1）* 0.75
• 离中趋势(数据离散程度的衡量，越大越离散，越小对于聚拢)：标准差、方差
• 数据分布：偏态和峰态、正态分布与三大分布

2、数据分布

偏态系数与峰态系数
偏态系数(skew)：数据平均值偏离状态的一种衡量，偏>>平均值的偏，越小越好
下图是偏态+正偏，
第一根线是中位数，均值为第二在中位数右，so正偏

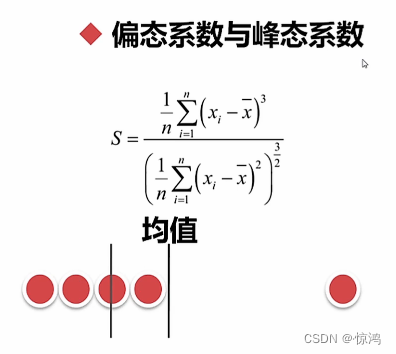
峰态系数(kurt)：数据分布集中强度的衡量,0为标准

• 值越大，顶越尖

• 值越小，越平滑，像小山丘 or 平地 一样
  
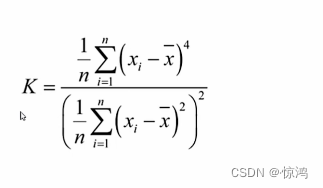
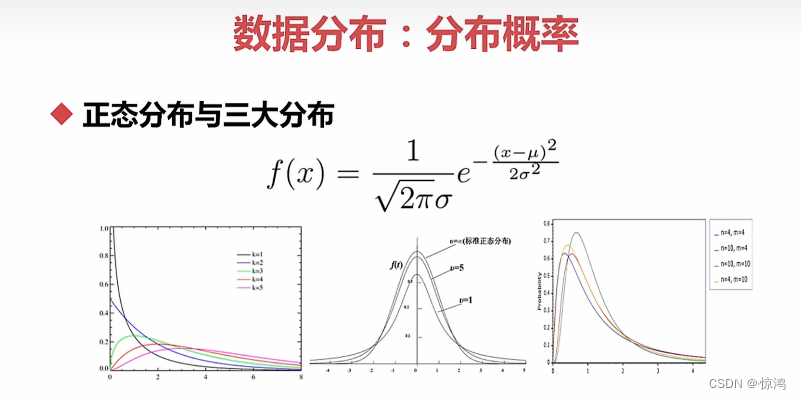
  正态分布和三大分布
  标准正态分布：方差、标准差是1、均值是0

• 卡方分布：几个标准正态分布（均值为0方差为1）的平方和满足的分布

• T分布：正态分布的一个随机变量除以一个服从卡方分布的变量----用来根据小样本来估计呈正态分布且方差未知的总体的均值。

• F分布：构成两个服从卡方分布的随机变量的比值构成的（即就是两个卡方分布的商）

3、抽样理论

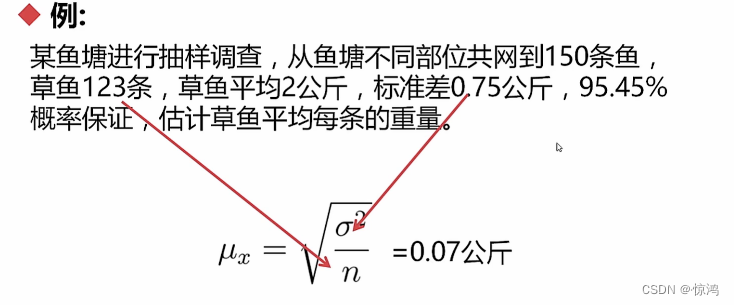
抽样误差与精度

例子1

例子2

代码实现

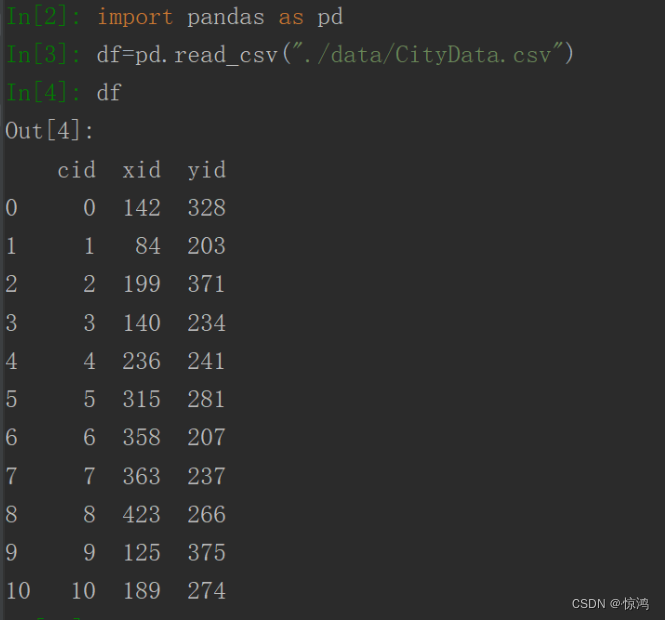
分别输入type(df)和type(df["cid"])可以发现两种数据类型不同

计算平均值：df.mean()或df["xid"].mean()

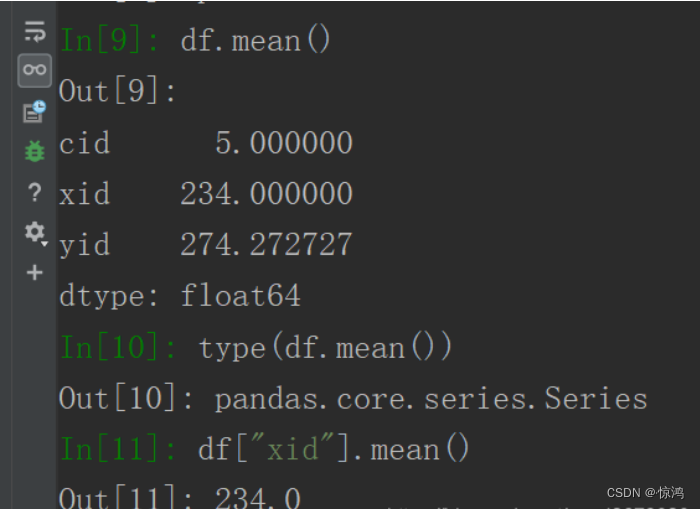
计算中位数：输入df.median()或df["yid"].median

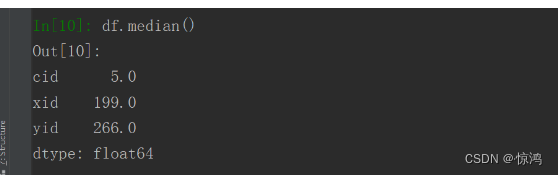
求四分位数：输入df.quantile(q=0.25)

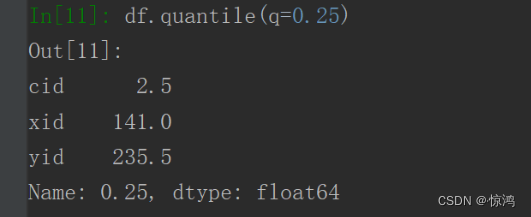
求众数：输入df.mode()或df["xid"].mode()

求标准差：输入df.std()或df["yid"].std()

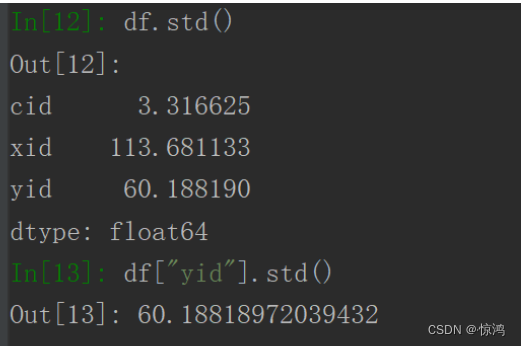
计算方差:df.var()或df["xid"].var()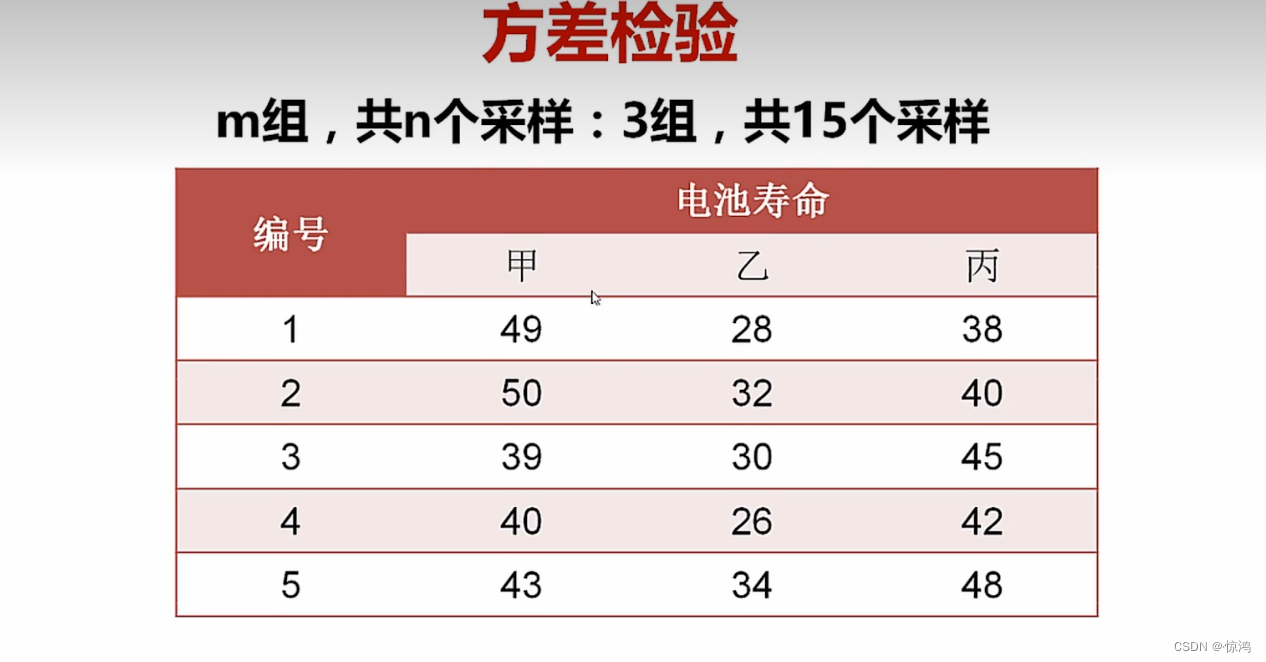

求和：df.sum()或df["xid"].sum()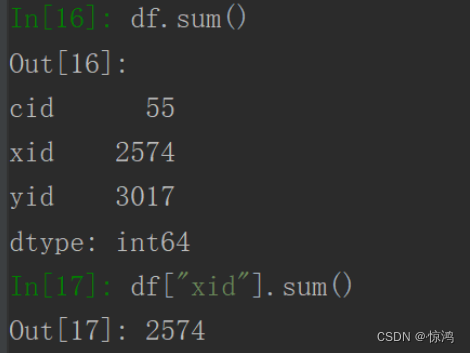

计算偏态系数：df.skew()或df["yid"].skew()

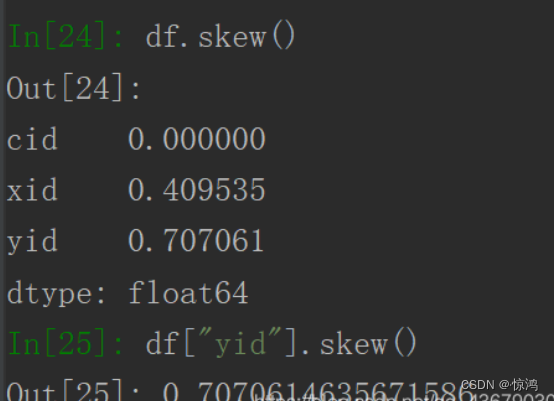
计算峰态系数：df.kurt()或df["yid"].kurt()

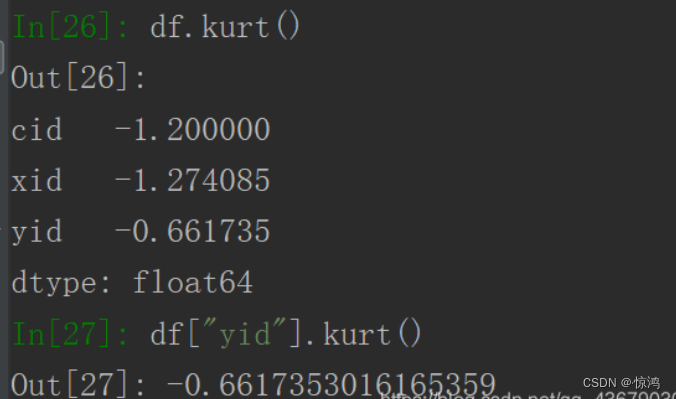
生成正态分布函数，pandas无法直接生成，需要先引入scipyimport scipy.stats as ss，再输入ss.norm，这时生成的是一个正态分布的对象
我们输入ss.norm.stats(moments="mvsk")查看一下，mvsk分别代表的是均值、方差、偏态系数、峰态系数

这时我们可以看到生成四个值，分别对应正态分布的mvsk分别为0、1、0、0。

• ss.norm.pdf(0.0)表示横坐标为0时的纵坐标的值
• ss.norm.ppf(0.9)表示从负无穷累积到返回值时得到的值为0.9，其中ppf后的值必须在0-1之间
• ss.norm.cdf(2)表示从负无穷积分到2时的返回值
• ss.norm.rvs(size=10)可以得到10个随机的符合正态分布的数字

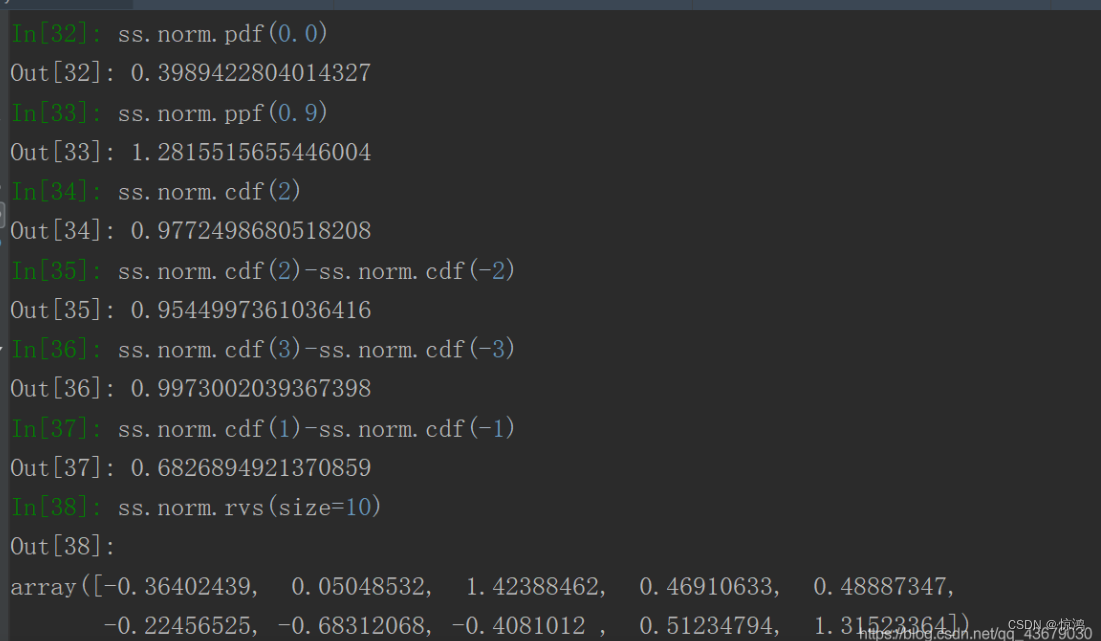
类似的，我们可以分别输入ss.chi2和ss.t得到卡方分布和T分布

此外我们还可以进行抽样

• 输入df.sample(n=10)从数据中抽取10个样本
• 输入df.sample(frac=0.1)从数据中抽取10%的样本
  

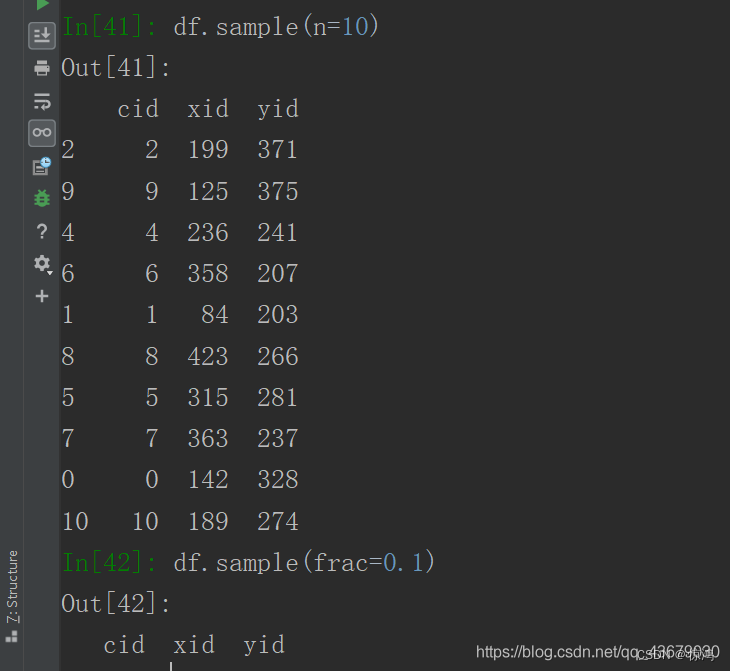
4、数据分类

1. 定类（类别）：根据事物离散，无差别属性进行的分类（性别、民族）
2. 定序（顺序）：可以界定数据的大小，但不能测定差值（收入的高、中、低，但是具体高多少，无法用具体数字表明）
3. 定距（间隔）：可以界定数据的大小，可以测量差值，但是无绝对零点（乘、除、比率是没有意思的，比如：摄氏温度）
4. 定比（比率）：可以界定数据的大小，可以测量差值，有绝对零点（身高、体重、长度、体积）

5、单属性分析

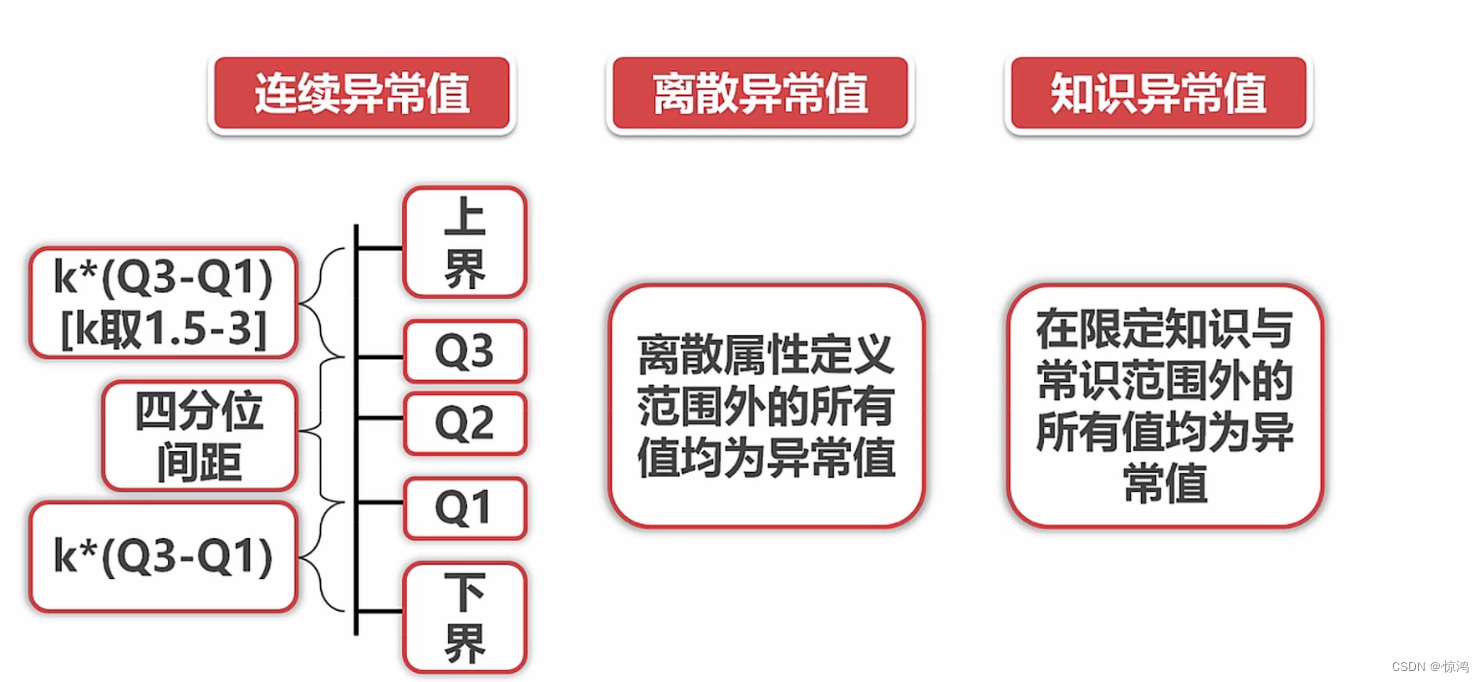
1. 异常值分析：离散异常值、连续异常值、知识异常值
2. 对比分析：绝对数与相对数，时间，空间，理论维度比较
3. 结构分析：各结构的分布和规律
4. 分布分析：数据分布频率的显式分析
   

相关解释课题

分析类别详解

对比分析
通过比较的方式，达到了解与认识数据和事实的分析方法
比什么

怎么比
时间：同比，环比
空间：显示方位：不同城市、国家、城市，逻辑：不同部门
经验与计划：历史上失业率达到多少就会发生暴乱，我们把自己国家拿去比较就是经验
做工作要排期，我们自己工作要和排期作比较就是计划

结构分析
可以看作对比分析中的比例相对数的比较，它重点研究一个总体的组成结构方面的差异与相关性
分为：

• 静态结构分析：直接分析总体的组成，比如我们直接分析十五期间第一、二、三产业比率为13%、46%、41%，我们可以拿这个和美国、印度比，来衡量我们三大产业是否均衡，下一步该怎么决策等
• 动态结构分析：以时间为轴分析结构变化的趋势，比如我们知道十五期间三大产业的占比，那么对于十五期间三大产业是怎么变化的，就能反映我们国家性质上的变化方向，第一产业大幅度降低，第二产业增高，而第三产业大幅升高，这就说明了国家在转型（当然这是例子嗷，不是事实）

分布分析

实例运用

定义异常值的范围

• n的范围为：1.5倍 - 3倍

1. 四分位间距：上四分位数 - 下四分位数
2. 上界：上四分位数 + n* 四分位间距
3. 下界：下四分位数 - n* 四分位间距

• 上下界之间的我们可以叫做正常值，以外的我们可以叫做异常值
  1、saticfaction_level（满意度） 字段分析
  

依次为：
满意度、最近的一次评价、做的项目数量、每个月的工作时长、在公司的时间、是否发生事故、是否最近有离职、最近五年是否有提升、部门、薪水

去掉异常值
满意度
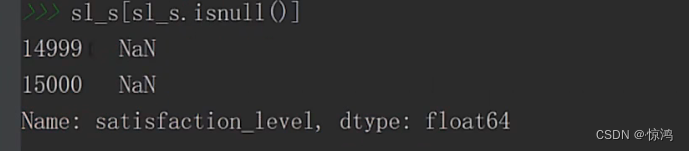
isnull（）：可以列出是否有空值

可以看出至少有两个

当然上面显示不完全，我们可以指定查询条件，我们发现，为空的记录只有有两条

我们可以在源数据里面查看，一样的道理，也是指定条件，如下

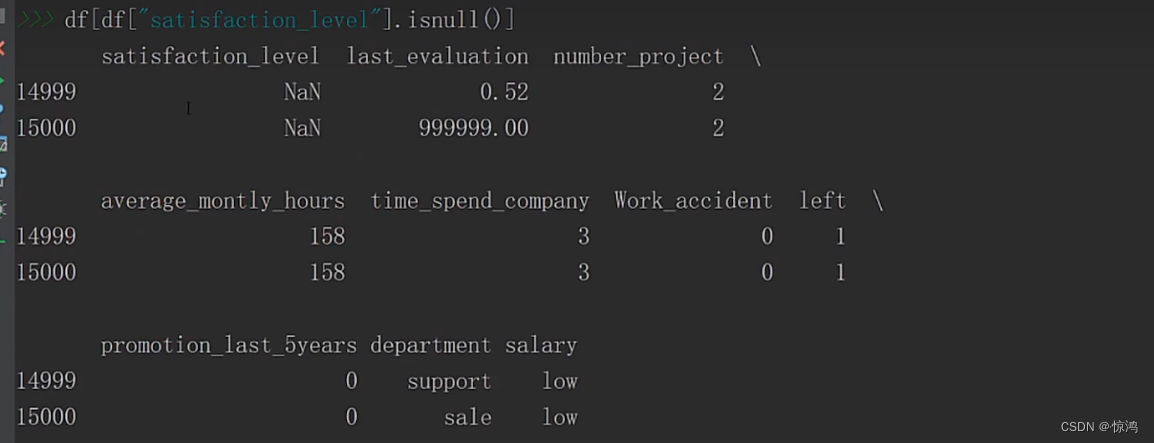
我们可以丢弃
dropna：删除异常值
fillna：填充异常值

丢弃之后我们再来看
刚才的两条异常数据就被丢弃了

查看均值、标准差、最大值、最小值、中位数、下四分位数、上四分位数、偏度、峰度
最大值和最小值可以看出这个数据大约就是1到0.9之间的分布了

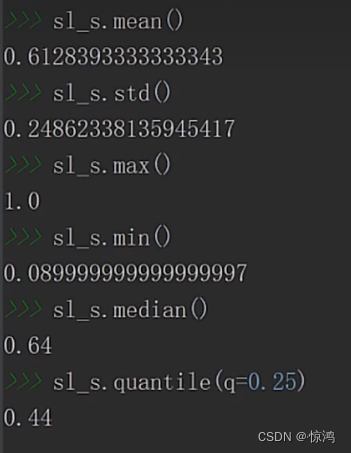
上四分位数 - 下四分位数的值为0.38，向上数都可以覆盖到我们的最大、最小值，so应该没多大问题

偏度为负偏度，他的均值是偏小的，大部分数是比他的均值要大的，
峰度为比较平坦的状态

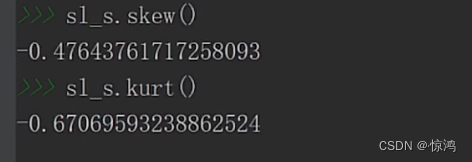
0-0.1 之间的数有195个
0.1 - 0.2 之间的数有1214个
以此类推
符合负偏形状

np.histogram函数

np.histogram()是一个生成直方图的函数

histogram(a,bins=10,range=None,weights=None,density=False)
1

• a是待统计数据的数组；

• bins指定统计的区间个数；

• range是一个长度为2的元组，表示统计范围的最小值和最大值，默认值None，表示范围由数据的范围决定

• weights为数组的每个元素指定了权值,histogram()会对区间中数组所对应的权值进行求和

• density为True时，返回每个区间的概率密度；为False，返回每个区间中元素的个数

a = np.random.rand(100)
hist,bins = np.histogram(a,bins=5,range=(0,1))
print(hist)
print(bins)
1
2
3
4
1
2
3
4
5
6
7
8

输出：

[19 30 15 16 20]
[ 0.   0.2  0.4  0.6  0.8  1. ]
1
2

2、LastEvaluation（最近的一次评价） 字段分析
空值
我们再来看另外一个指标

可以看出，这个字段没有 空值

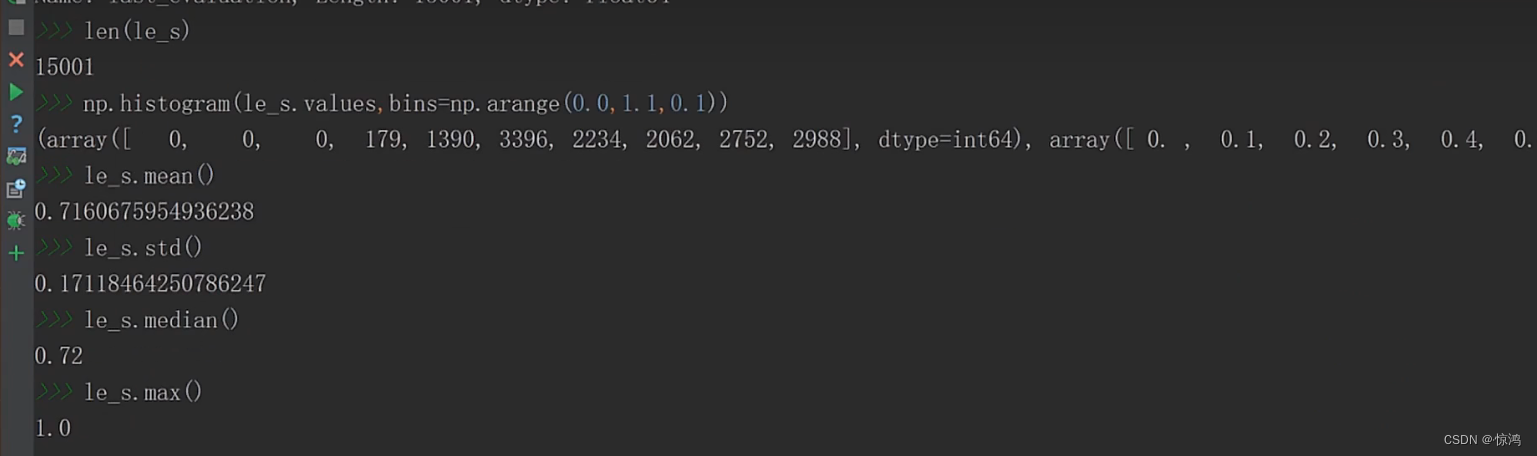
从均值我们就觉得有点离谱，在看到我们的最大最小值，数据相差非常大
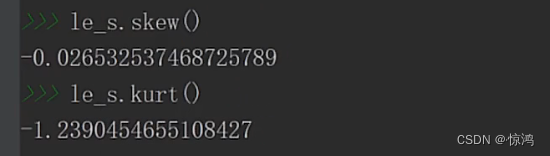
在看到我们的偏度，属于极度正偏，均值比大部分值多很多
峰度：分布频变是非常大的，so应该是不靠谱的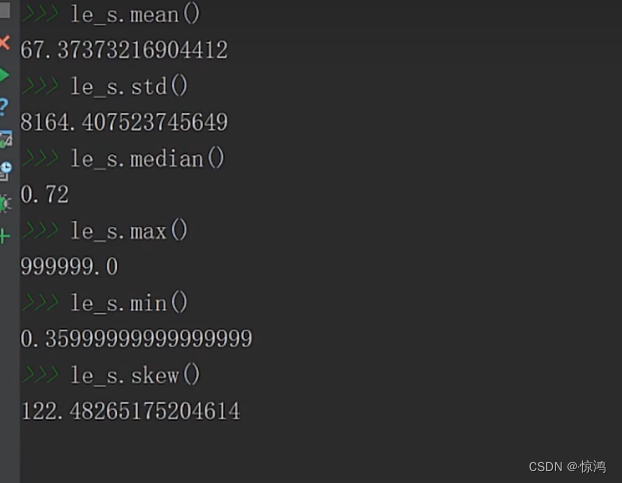

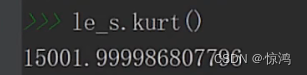
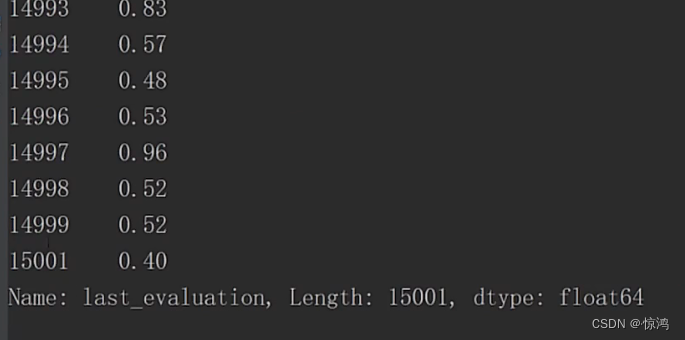
所以我们就来看看数据
查看大于1的数据，只得出一个，对于这种偏离的值，我们就有理由把他抛弃掉

删除数据

处理异常值
我们异常值的范围如果没指定具体数字，我们可以用一般的范围，如：

1. 算出我们的四分位间距
2. 上界的范围：上四分位数 + n倍四分位间距
3. 下界的范围：下四分位数 - n倍四分位间距
4. n的范围为 1.5 - 3
   我们这里设定倍数为1.5倍，我们允许的形变是比较小的，然后直接保留在我们这个范围里面的数据
   

删除后可以看出，我们的异常值数据已经没有了

3、NumberProject（做的项目数量） 字段分析
空值
可以看见，没有空值

查看指标

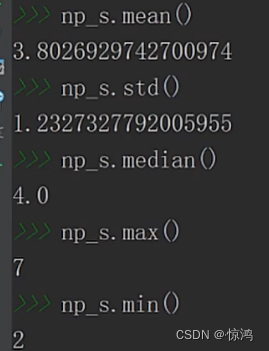
稍稍有点正偏，说明有些人的项目数量比平均值要少
峰态比较平缓

查看项目数量各有多少个

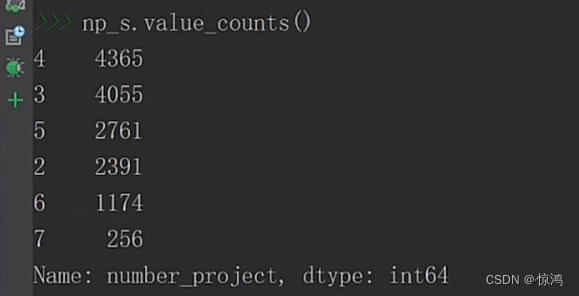
其实个数我们有时候不是太关注，我们需要更直观的东西：比例

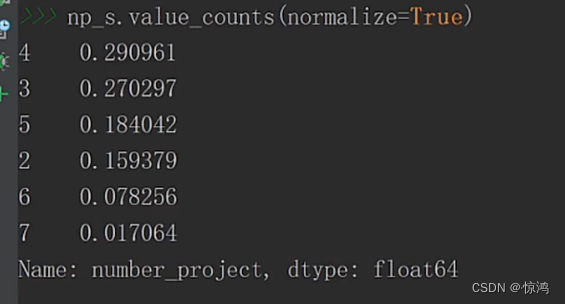
在排一下序

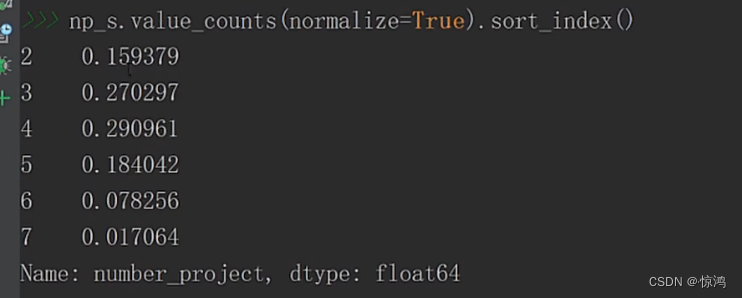
其实这上面叫做 静态结构分析
4、AverageMonthlyHours（每个月的工作时长，小时）字段分析
依次为：
满意度、最近的一次评价、做的项目数量、每个月的工作时长、在公司的时间、是否发生事故、是否最近有离职、最近五年是否有提升、部门、薪水
指标
稍稍正偏

峰度比较平缓（小于3），说明他的聚拢程度稍微差一些

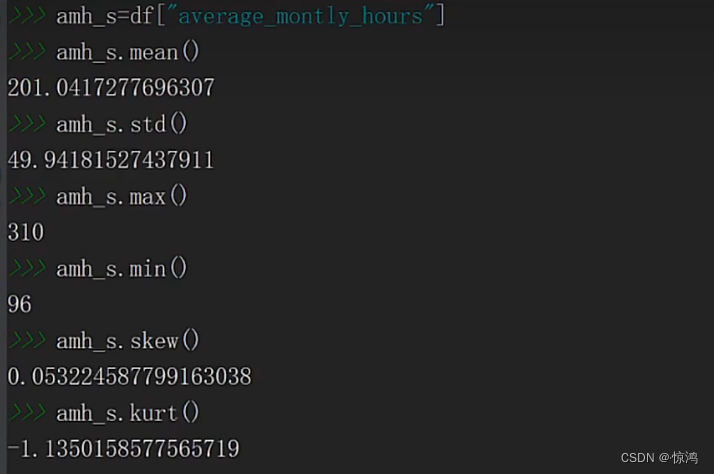
处理异常值
这玩意你们看得懂把 就是和上面一样，只取我们正常值范围的数据


去除过后

画个直方图瞅瞅

np.histogram 的bins 是左闭右开
value_counts 的bins 是左开右闭
1
2

5、timespendcompany（在公司的时间）字段分析
依次为：
满意度、最近的一次评价、做的项目数量、每个月的工作时长、在公司的时间、是否发生事故、是否最近有离职、最近五年是否有提升、部门、薪水

6、Workaccident（是否发生事故） 字段分析
依次为：
满意度、最近的一次评价、做的项目数量、每个月的工作时长、在公司的时间、是否发生事故、是否最近有离职、最近五年是否有提升、部门、薪水

看得出来符合字段要求，即无异常值
发生事故的概率

7、Left（是否最近有离职）字段分析

依次为：
满意度、最近的一次评价、做的项目数量、每个月的工作时长、在公司的时间、是否发生事故、是否最近有离职、最近五年是否有提升、部门、薪水

符合字段要求

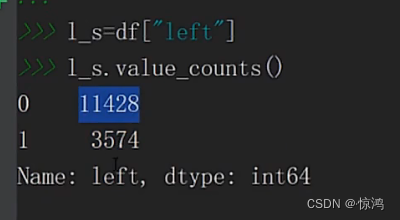
8、PromotionLast5Years（最近五年是否有提升）字段分析

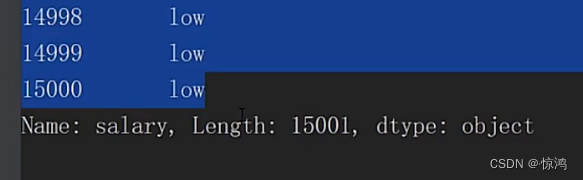
9、Salary（薪水）字段分析
我们发现出现了 nme这个异常值

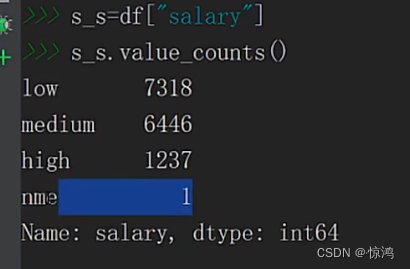
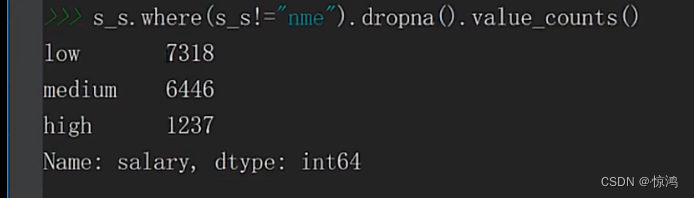
首先我们肯定要先找到它对吧，使用 where 方法实现找指定值显示本来值，可以看出在15001行，其他值填充为NaN
这里取反就刚好把异常值 变为NaN，其他正常值不变，再使用我们的dropna 方法，删除NaN值
就达到我们删除异常值的目的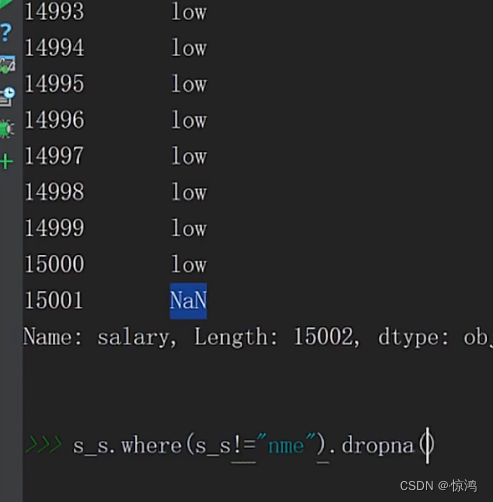

删除后如图

最后再查看一下，保证结果的正确

10、Department(部门)字段分析
value_counts(mormalize=True)：表示显示出各个部分所占的比例

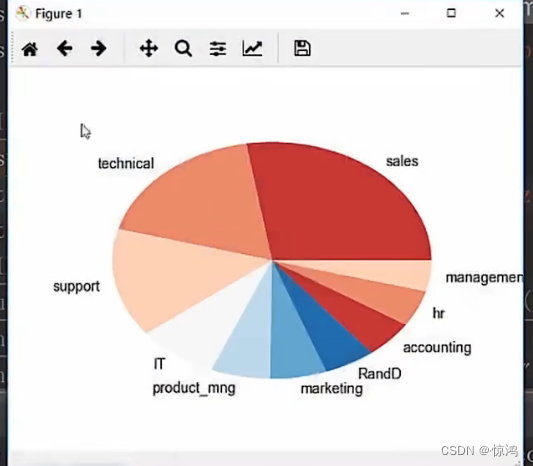
如图
我们可以发现有 sales和sale字段，我们猜测是录入的错误，但是我们要根据实际业务情况，给你任务的人不至于不说是吧？
so，我们在这里就认为 sale 是异常值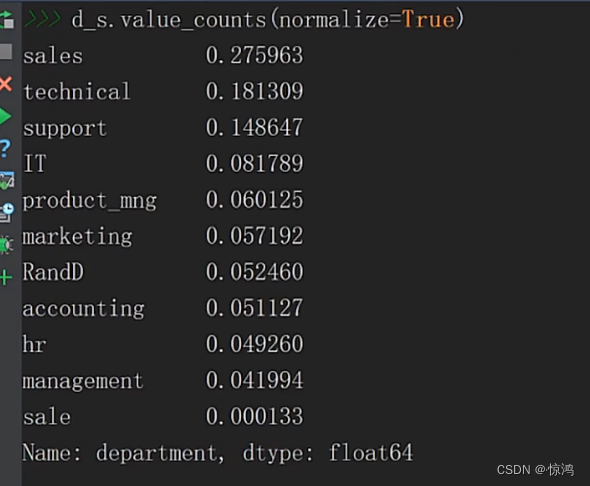

那就简单了呗，上面才讲解

简单对比分析操作

首先还是去除空值
dropna 有两个参数

• axis：取值有 0，1。0代表按行，1代表按列，意思说我们是删除这一行，还是这一列
• how：取值有all，any。all代表如果这一行\列 全部都是空值，我们就删除；any是代表如果有空值就删除
  
  这里我们就删除了15000这条空值
  
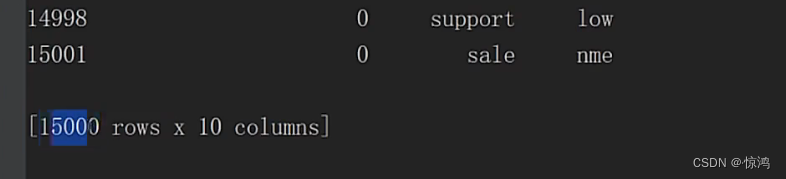
  接下来再继续做我们上面所分析的异常值
  
  这里我们所有分析出来的异常值就全部删除掉了
  
  现在我们就可以进行分析了
  先来做个简单的对比分析，我们可以看到department部门字段分了很多部门，我们就以部门字段分析
  取个平均值，非数字数据这里就会自动删除咯

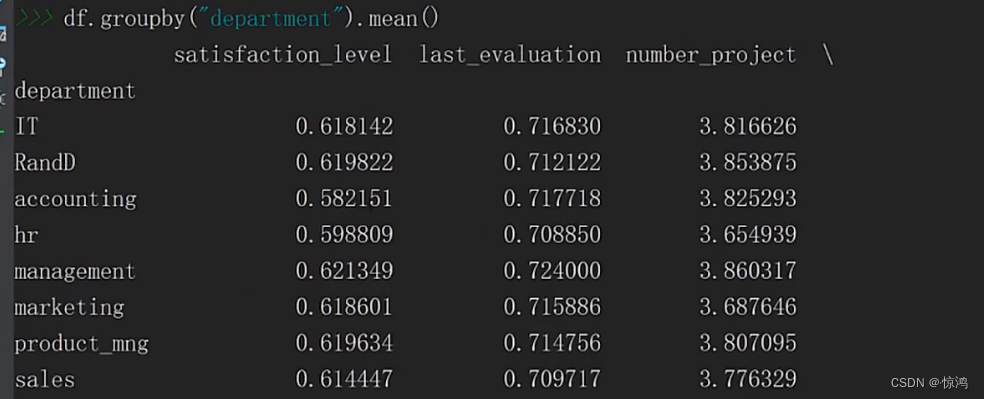
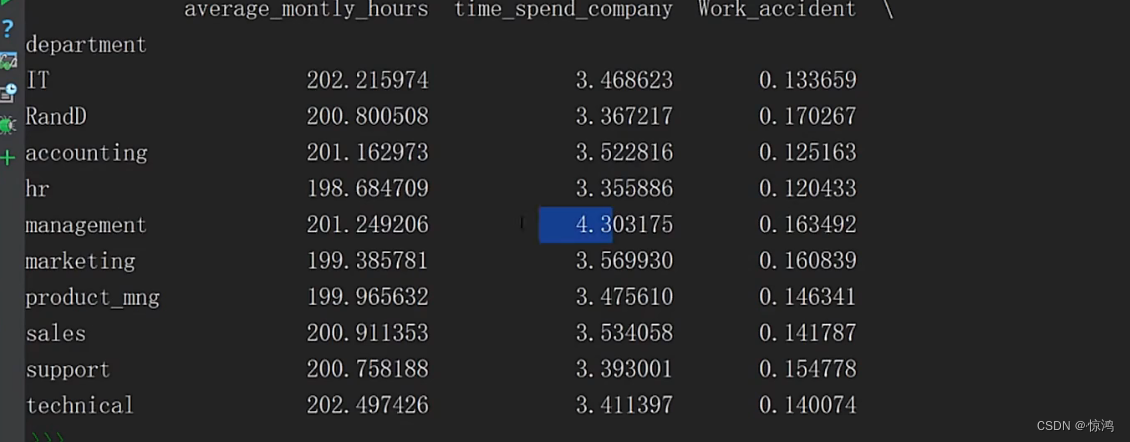
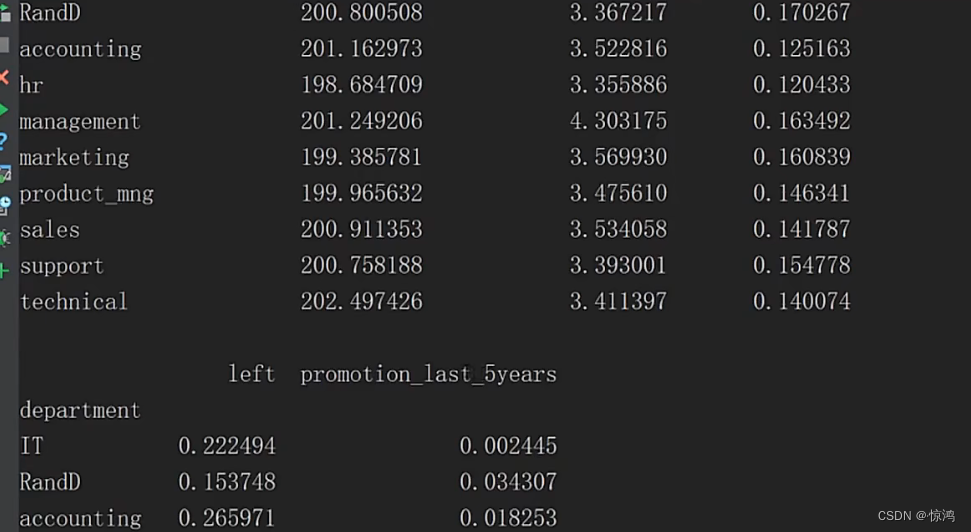
上面是全部字段一起对比分析，我们可以单独弄出来一些字段分析

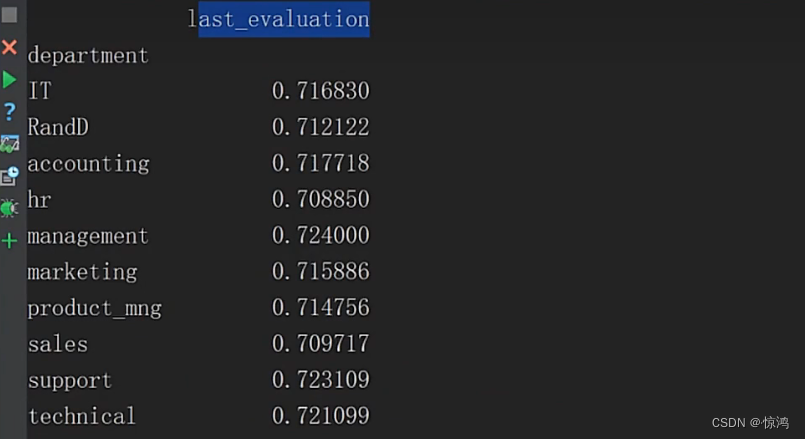
看的懂吧
先把这两个字段单独取出来，再按部门分组
再取 这个字段的值

然后，定义一个匿名函数，计算极值，极值就是最大值减去最小值呗

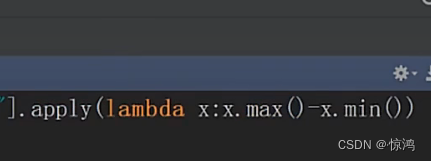
得到

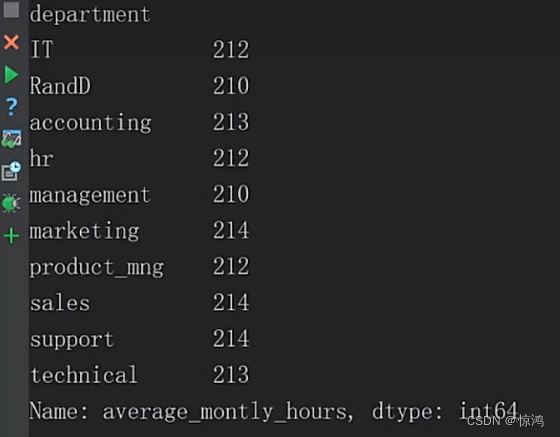
6、可视化

seaborn库 不仅可以自己画图也可以设置matplotlib的样子，就是封装的matplotlib
柱状图

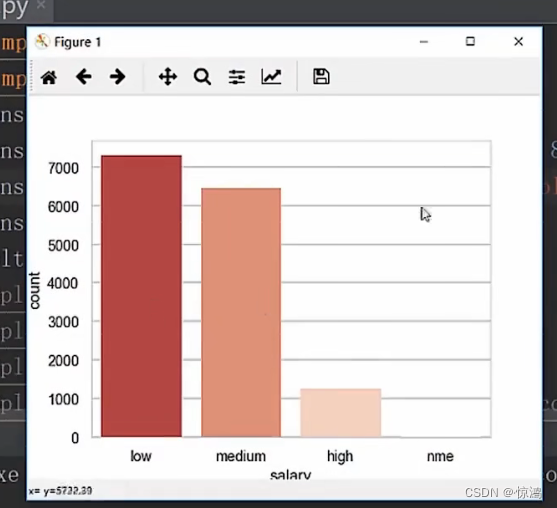
countplot还可以帮我们多层绘制

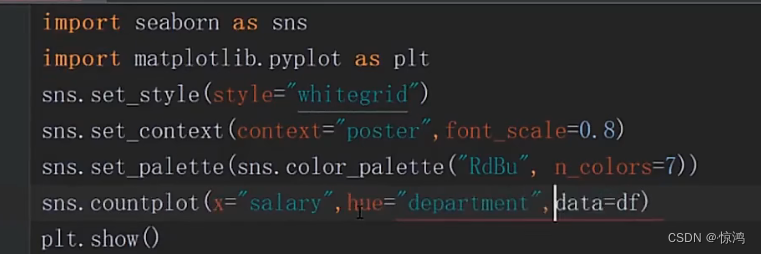
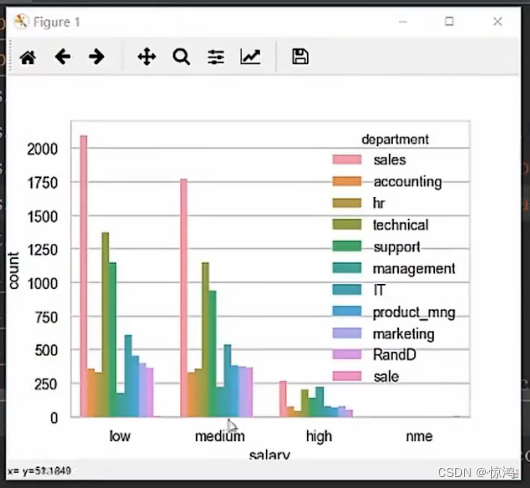
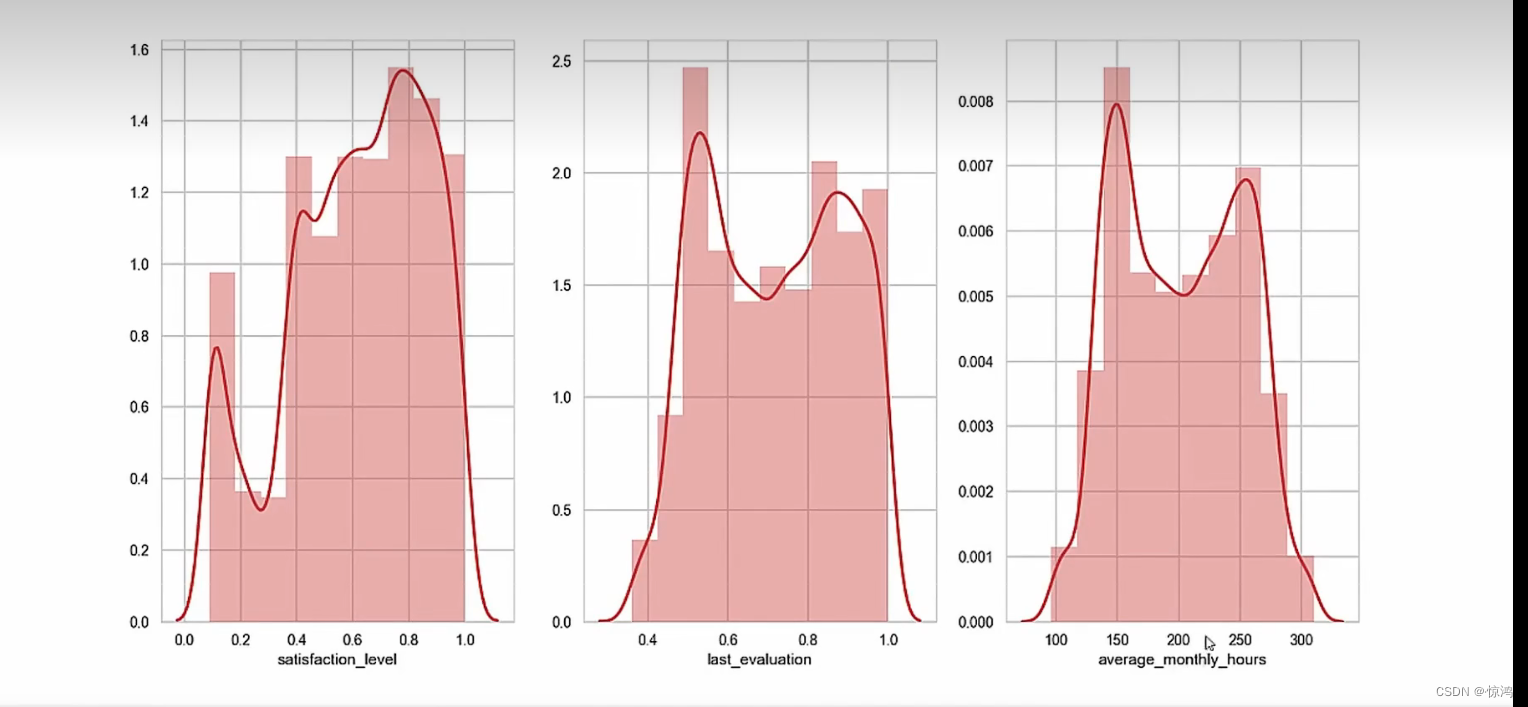
直方图

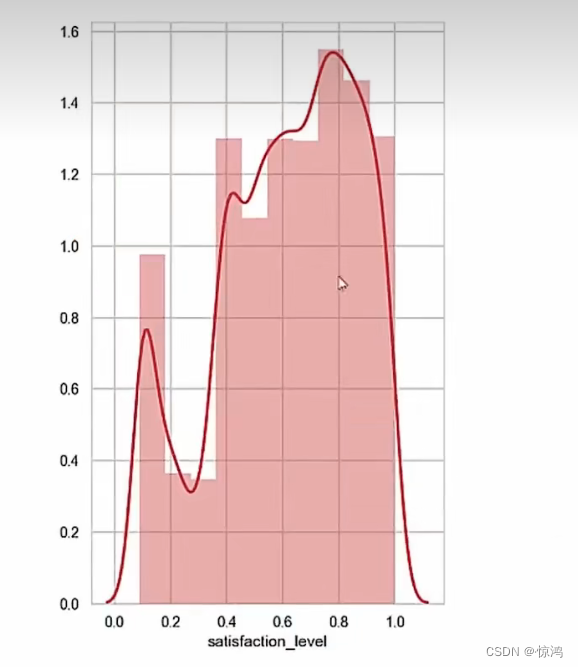
如果不要 曲线
设置 kde = false

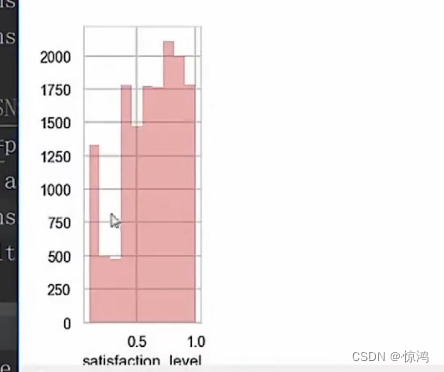
那反过来不要 图形只要曲线呢？
设置 hist = false

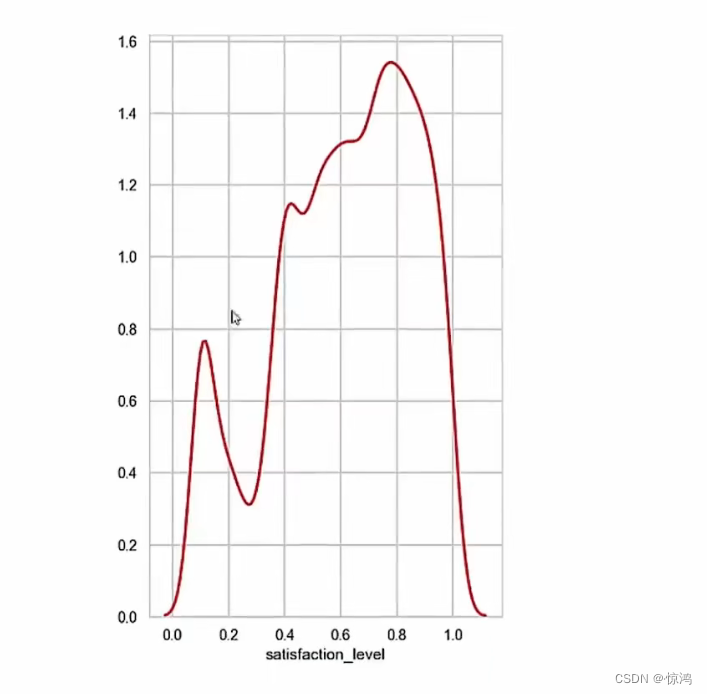
我们在加一个子图

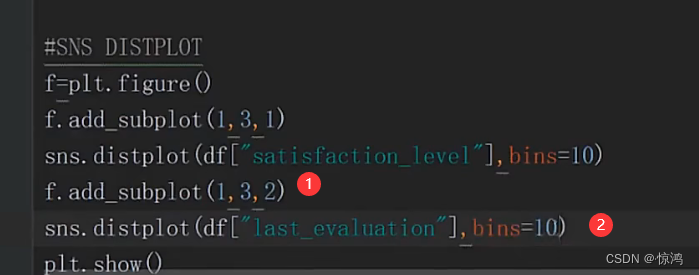
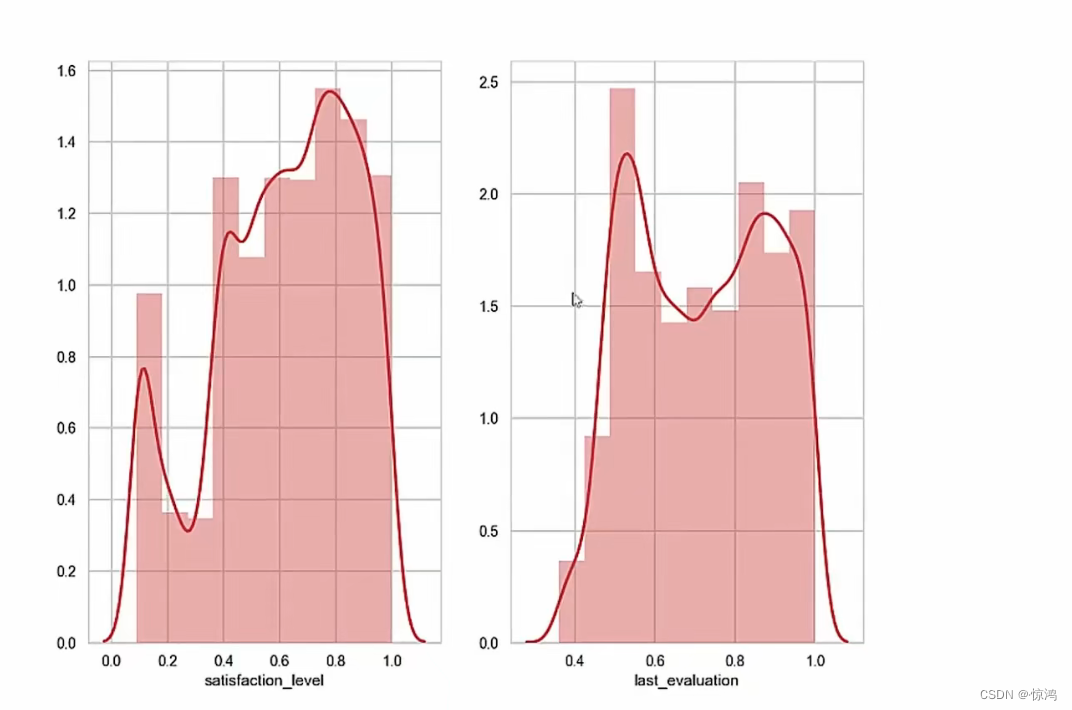
在加一个子图

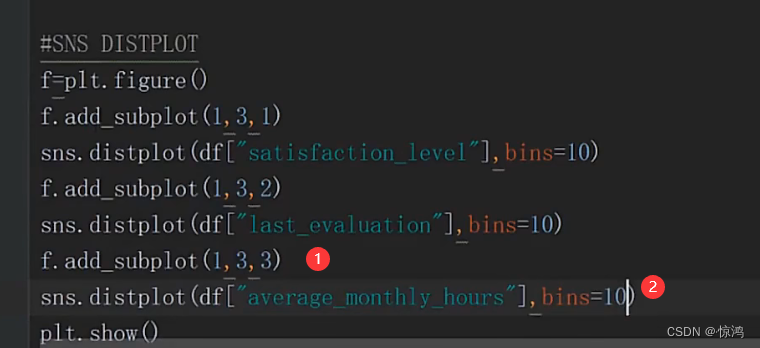
我们可以从第三图发现我们的工作时间是呈两级分布的

箱线图

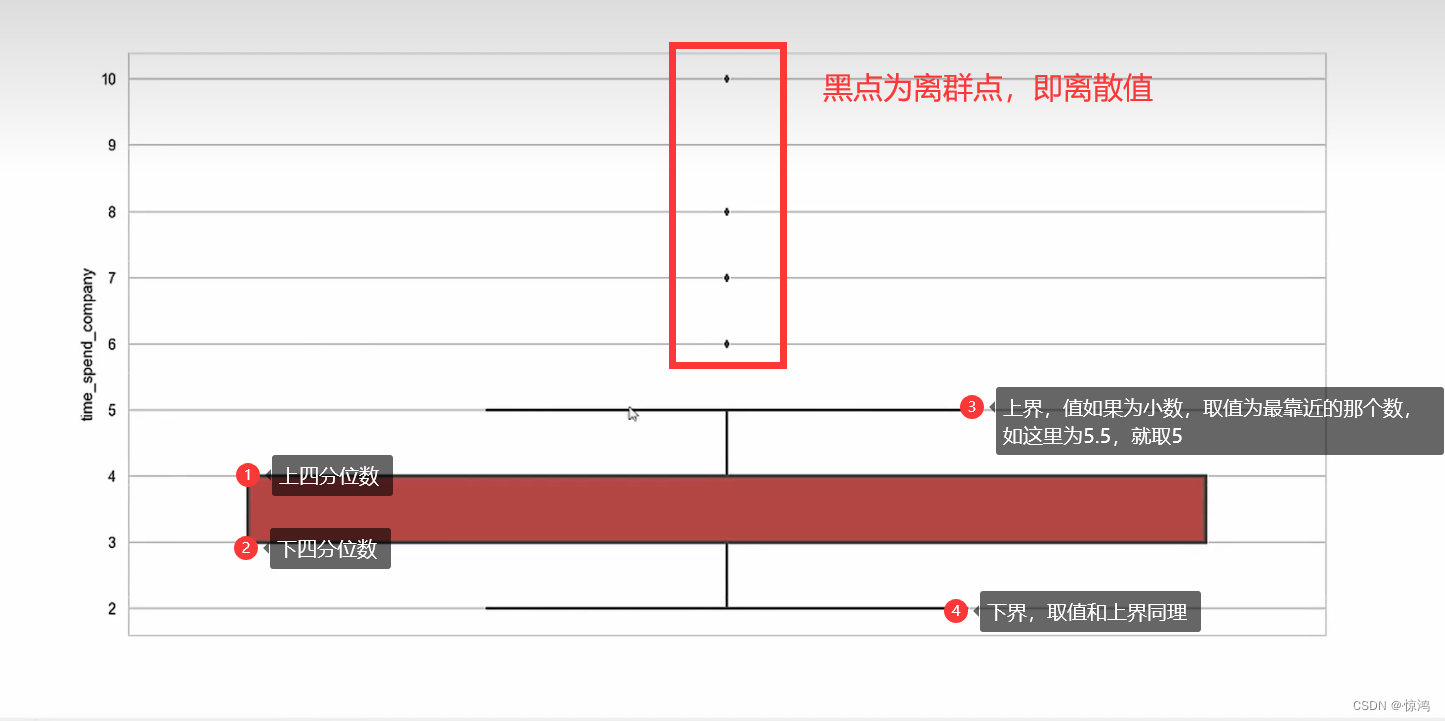
如图
我们发现 箱线图可以非常直观的把异常值区分出来

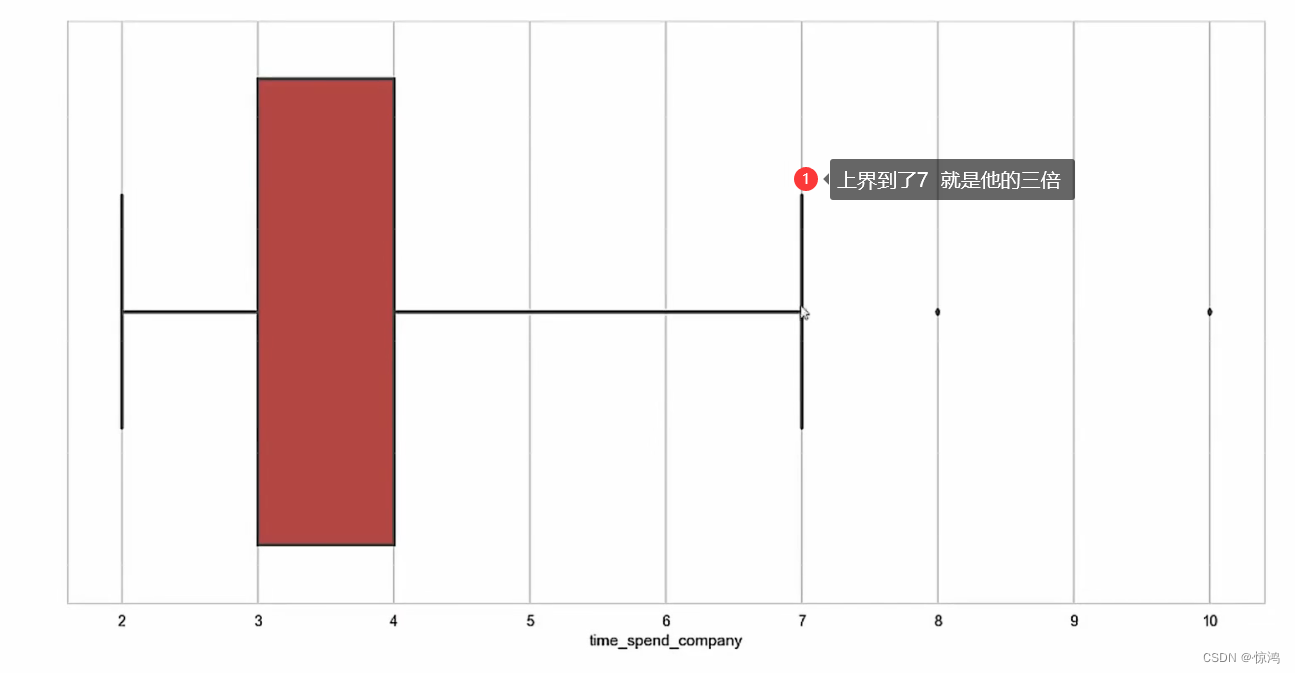
可以发现我们上面是赋值的 y 的值，那如果我赋值的是x的值呢？那图像就是横着的了
saturation = 0.75
whis = 3 3倍 也就是上面说的 边界距离，一般设置为1.5倍 ，这里我们可以指定，为3 倍

折线图

一般表示数据变换的趋势

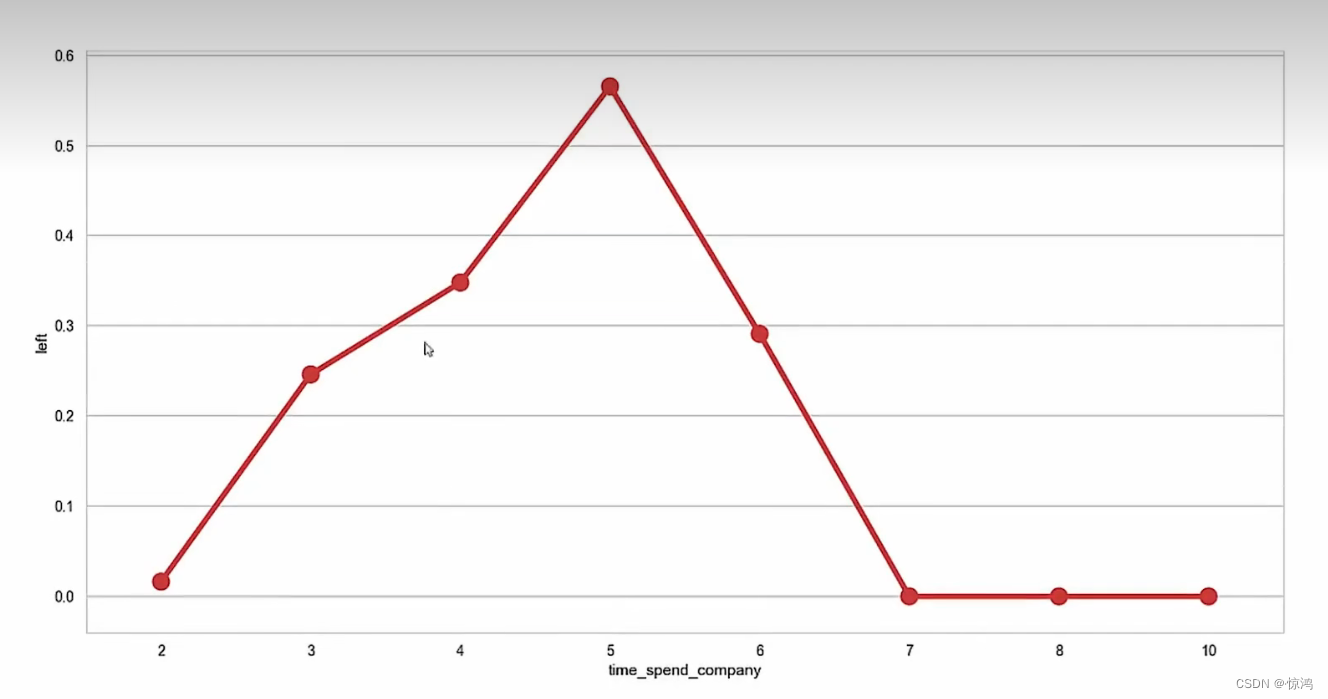
第二种

可以发现点多了一条线，这个可以帮助我们看清楚覆盖的范围

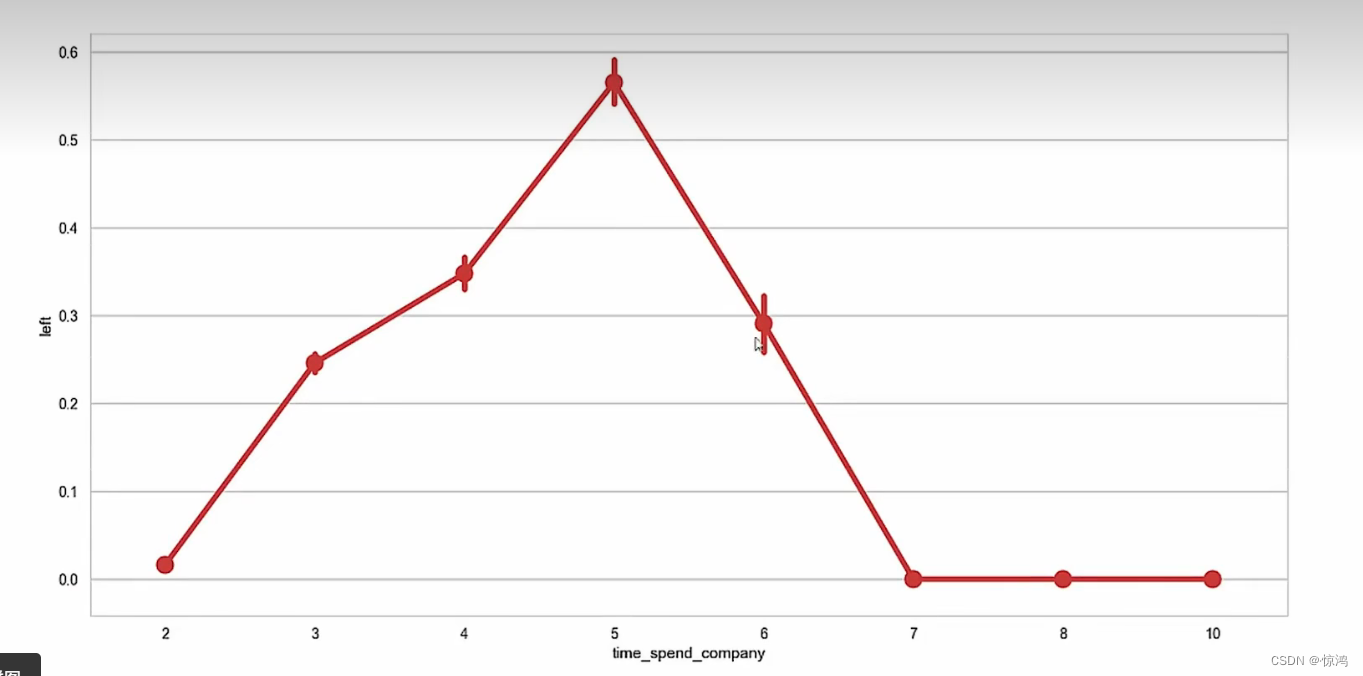
饼图

主要来做结构分析

可视化 请看我的matplotlib 文章

7、探索性数据分析（多因子和复合分析）

假设检验

1. 我们通常把假设和一个已知的分布联系起来
2. 一般情况下，原假设的设定为符合该分布，而备择假设 则不符合 该分布，so反命题
   
3. 根据我们数据的均值、方差等性质构造的一个转换函数
4. 构造这个函数的目的，是让这个数据符合一个已知的分布，比较容易解决的数据，比如，我把一些数据减去他的均值，再除以标准差这样判断这个转换后的统计量，也就是我们所说的检验统计量，是否符合标准正态分布，即可以判断数据的分布是不是正态分布的概率了

、

• 显著水平一般用 α （希腊字母阿尔法）表示，就是我们可以接受假设的失真程度的最大限度
• 显著水平和相似度的加和为1，比如，我们确定了某个数据属性有95%的概率是某个数据分布，那么他的显著性水平就是5%。如果有90%的概率是某个分布，那么他的显著性水平就是10%。
• 显著性水平一般是人定的值，值定的越低，相当于数据和分布的契合度就越高、
• 这个值我们一般取0.05,就是要求数据要有95%的可能和分布一致
• 一旦确定了显著性水平，那么在这个已知分布上就可以画出一段与这个分段相似的区域，我们叫做接受域，接受域以外的区域叫做拒绝域 ，如果检验统计量落入了拒绝域，那么H0就可以认为是假的，是可以别拒绝掉的

• 最后一步就是根据我们计算的统计量和我们要比较的分布的过程
  判断的思路有两种

1. 根据我们前面讲到的区间估计的方法，计算一个检验统计量的分布区间，看这个区间是不是包含了我们要比较的分布的特征
2. 计算p值，直接和显著性水平进行比较，这个p值可以理解为比我们计算出来的检验统计量结果更差的概率，如果，p值小于α（检验统计量）那么这个假设就会认为是假的

例子
比如，有一个洗衣粉制造厂，他不可能制造出的每一包洗衣粉重量都相同，那么根据经验，产出的洗衣粉规格均值为 500g，标准差为2g
现在 抽样 某一台机器产出的洗衣粉重量为

由此判断，这台机器是不是符合该洗衣粉厂的要求，我们来根据上面的方法来进行假设检验

• 确定原假设和备择假设

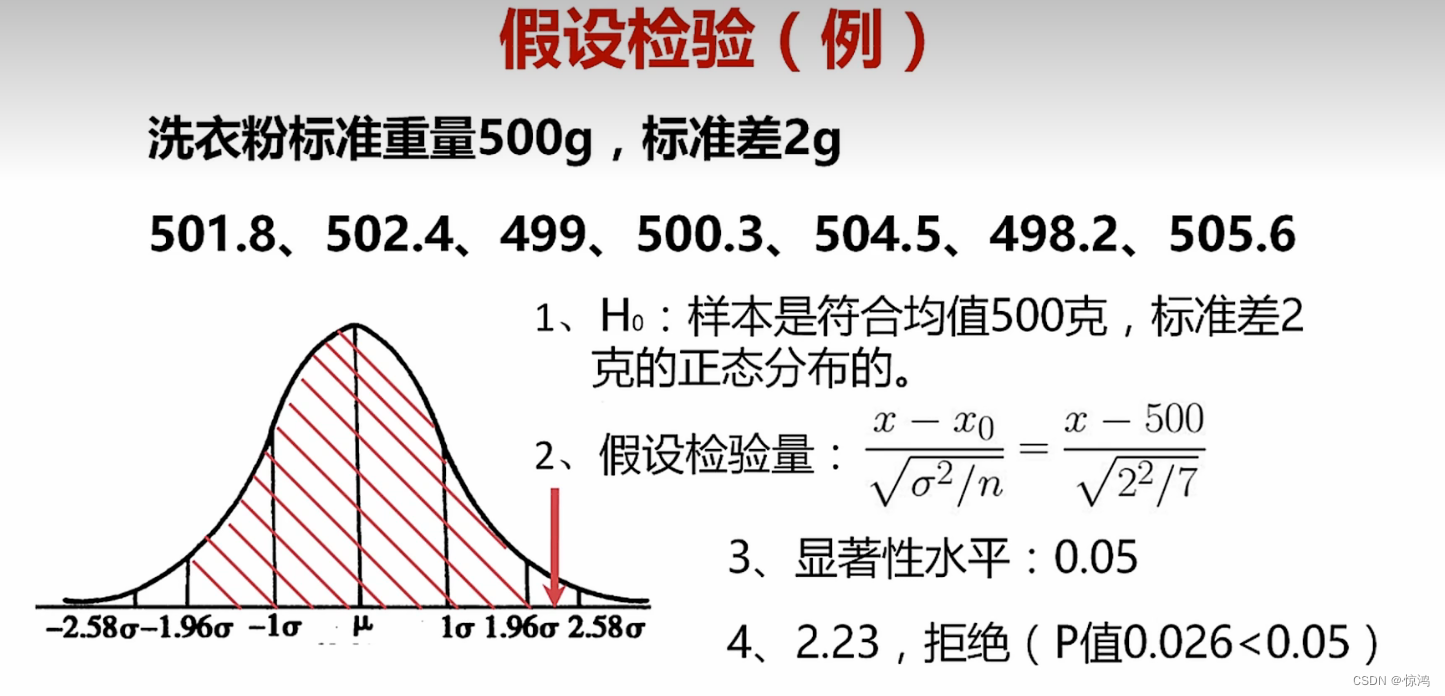
卡方检验

常用来检验两个因素之间有没有很强得联系
假设 化妆得人和性别关系不大
理论分布 为 55

计算出来

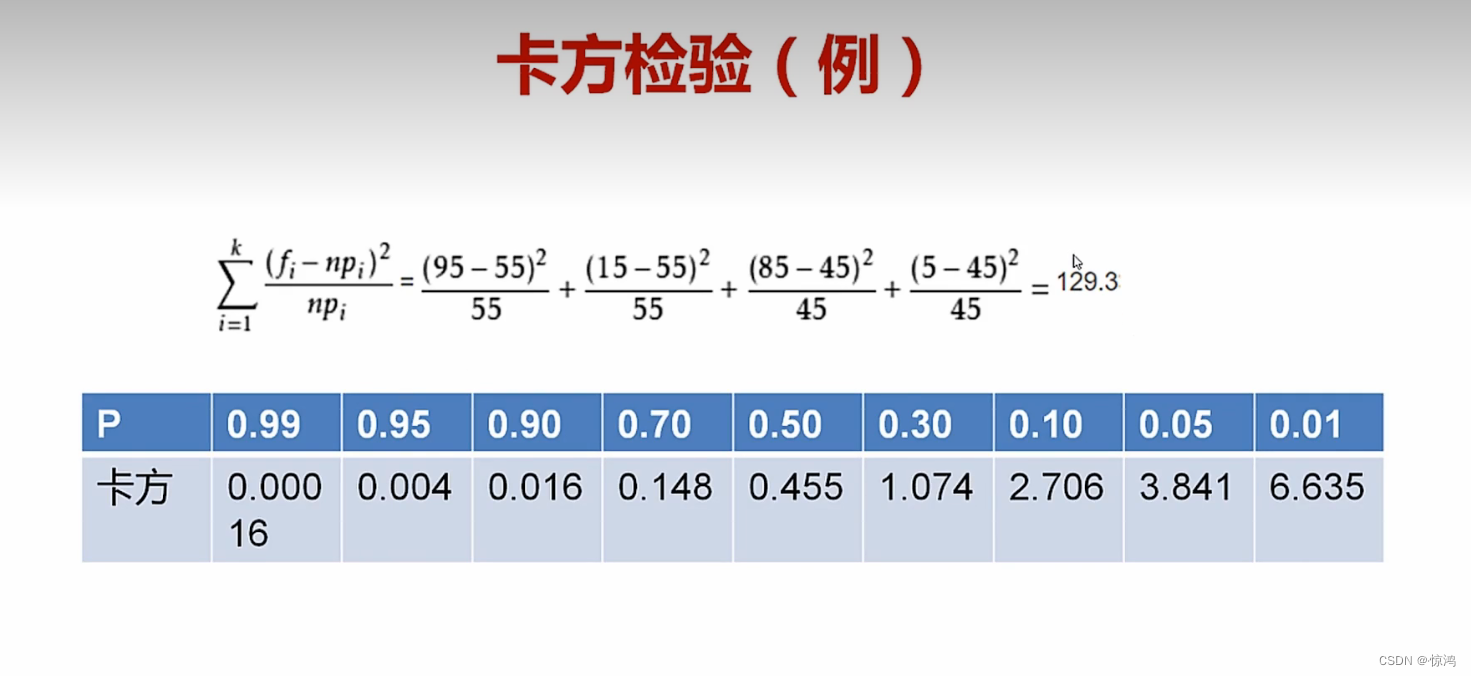
我们假设 显著水平为 0.05 ，这里算出来得卡方值为129.3，大于我们3.841，所以，我们推翻了我们得假设，即化妆人和性别有很大关系

方差检验

检验样本之间 两两是否有差异

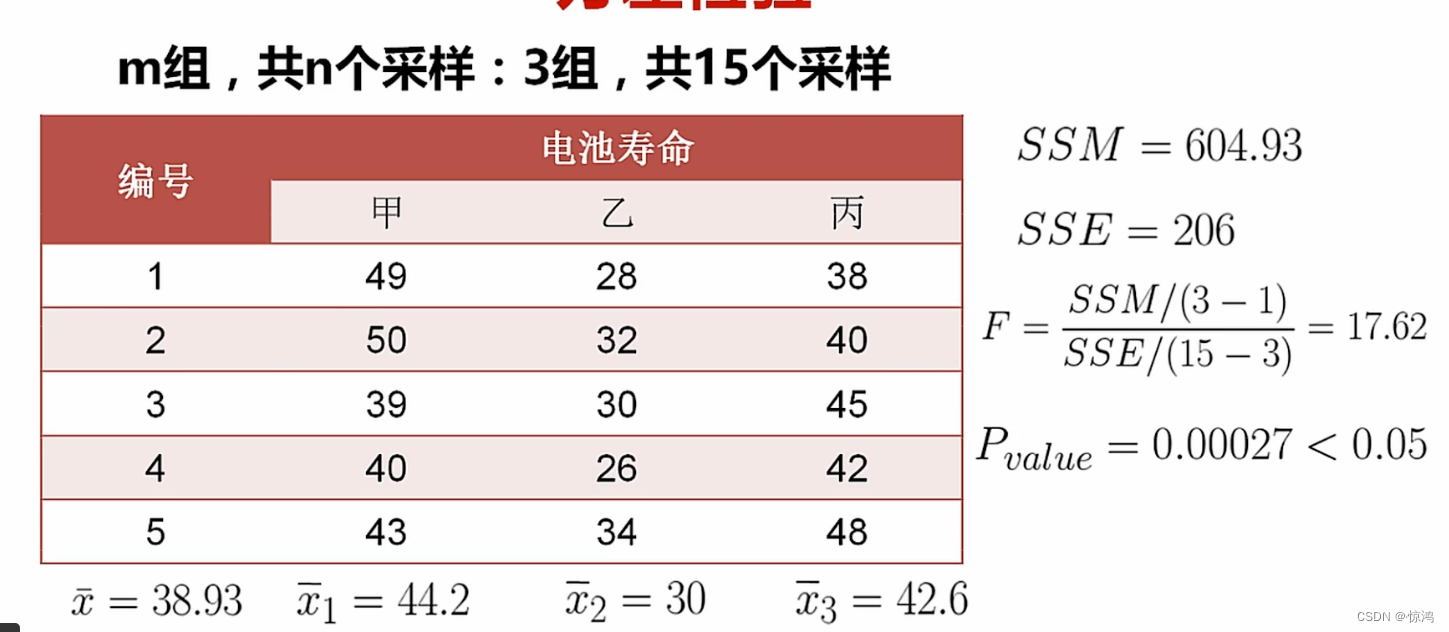
即他们三个得均值是有差异的

相关系数

第一个就是 皮尔逊相关系数
衡量两组数据或者两组样本得分布趋势、变化趋势、一致性程度得因子。
分为：

• 正相关、负相关、不相关

• 相关系数越大，越接近于1，二者变化趋势越正向同步，也就是说 一个变大，另外一个也变大，一个变小，另一个也变小

• 相关系数越小，越接近于-1，二者变化趋势越反向同步，也就是说 一个变大，另外一个就会变小

• 相关系数趋近于0，则认为两者是没有相关关系的

分子是两组数得协方差
分母是两组数得标准差得积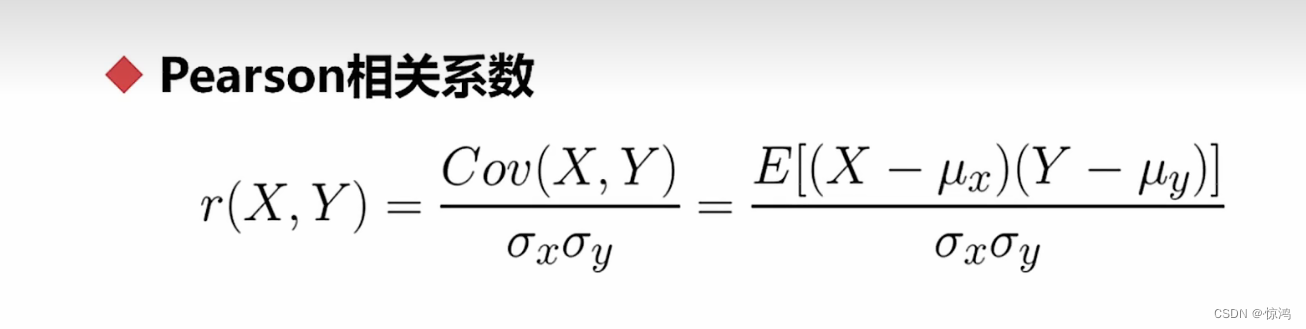

例子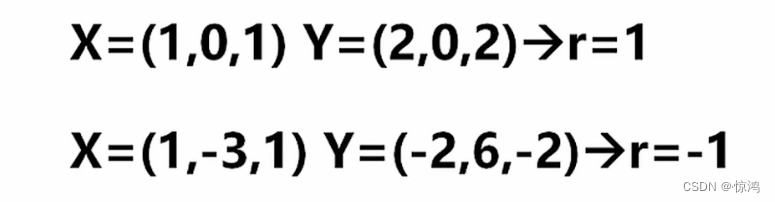

第二个为 斯皮尔曼等级相关系数
斯皮尔曼相关系数一般运用于相对比较

n是每组数据的数量
这里的d是指两组数据排名过后（小到大）的名次差

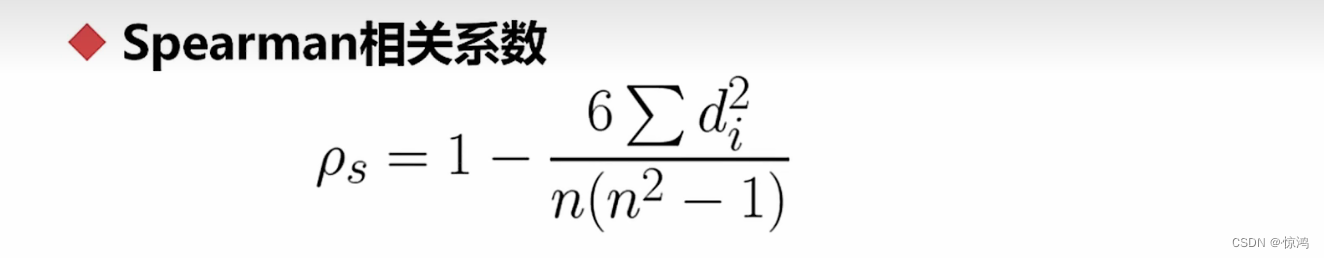
例子：

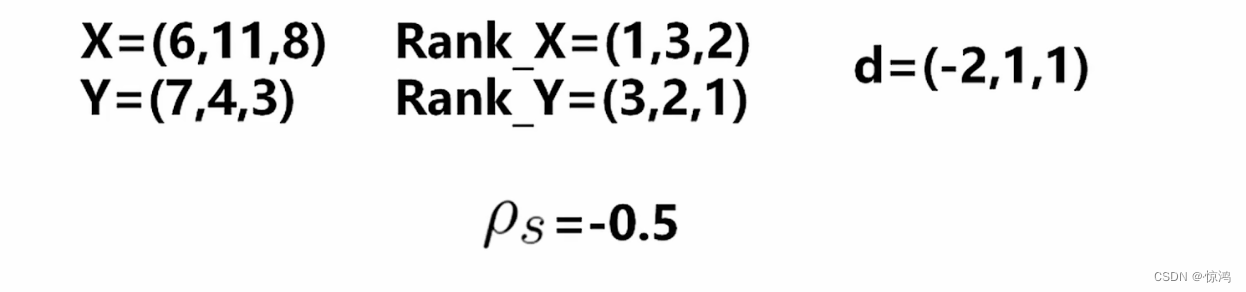
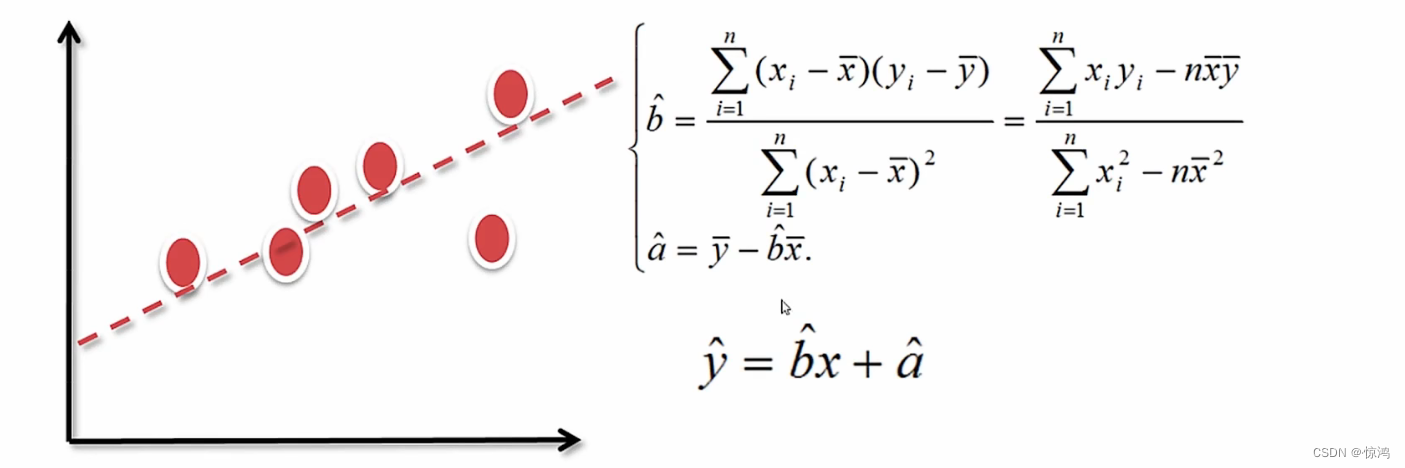
线性回归

** 什么是回归？**
回归就是：确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法
如果所谓的因变量和自变量的这种依赖关系是线性的话，那么就是线性回归

• 线性回归最常见的解法就是：最小二乘法，最小二乘法的本质就是最小化误差的平方的方法