python机器人编程——差速机器人小车的控制，控制模型、轨迹跟踪，轨迹规划、自动泊车（上）

一、前言

本篇我们依然试着用一些浅显的数学知识，来研究和实现一下常用机器人小车（如AGV）的控制，这里的小车我们先选用二轮驱动的差速小车，即通过两个驱动轮的转速控制实现所有想要的运动。我们会首先对这类小车的运动原理进行一些分析，并通过分析得出的数学步骤，用python去实现机器人小车的正向控制算法、反向控制算法（或者轨迹跟踪），并在此基础上，去尝试实现一下固定场景下，如仓储搬运、工厂转运等的机器人小车的轨迹规划、自动泊车（通常是去充电），并将首先在vrep仿真环境验证，验证完后，可以自己搭建实物去实现。

二、差速小车机器人的运动分析

如上图，我们研究的对象直观上是这样一个车，通过两个驱动轮电机控制去实现机器人小车的所有运动，当然实际中会加装一些摄像头、雷达等传感设备。
那么这样的小车我们分析一下，主要有这样的一些状态：

直观的看，小车可以有以上9种状态，前进（左前、右前、正前），倒退（左退，右退、正后退）、原地（左旋，右旋，停止），然后分别是通过左右轮的不同转速和旋转的方向的组合去实现这样的状态的。
其中这些状态，转向的实现是控制的重点。这里有一个前提是，假设在某个小间隔dt内，左右轮速度恒定，这样小车就在做圆周运动了。我们可以得出，当左轮和右轮产生速度差（线速度或转速）时候，小车就会转弯，当左轮的线速度值（不考虑方向）大于右轮时，小车转弯的半径、圆心在相对小车的右侧，反之，在小车的左侧，而且圆心始终在车轴的延长线上。
接下来来进一步研究：

三、正向运动控制模型推导

3.1问题描述

本节要解决的问题是，已知此时（t），小车的位置（x，y）和方向（小车YY轴与x轴的夹角），在某个小时间间隔（dt）内，给定两车的转速（sl、sr），在下个时刻（t+dt），小车的位置会在哪里？

3.2符号定义

如上图，首先来定义一下坐标系：我们定义大地坐标系为X-Y坐标系，用于定位小车中心的位置和方向信息，小车自身的坐标系为xx-yy坐标系，用于定位下一时刻小车的位置信息。本篇所用到的符号系统定义如下：
符号说明（不区分大小写）：
Rw：轮子的半径，已知
L：轮子距离，已知
ω ：车子中心的角速度，逆时针为正
Vc：车子中心的线速度，
Vl：车子左轮的线速度，
Sl: 左轮的转速，则：vl=sl2ΠRw
Vr：车子右轮的线速度，
Sr：右轮转速，则：vr=sr2ΠRw
R：t到t+dt时刻内，车子的圆周运动半径
θt：当前时刻的小车朝向，
θ(t+dt)：dt后的小车朝向，
dθ:dt内的转角
α:下一时刻位置点到小车原点连线与小车xx轴的夹角

3.3算式推导

基于上面的分析，我们首先来推导一下，小车圆周运动的圆心在小车右侧的情况（如上图，条件是|Vl|>|Vr|），步骤如下：

Step1 寻找数量关系，求出圆周半径，角度变化

假设t到t+dt时刻，小车的左轮速度为vl，右轮为vr，小车在以半径为R的圆周运动，当两个轮子产生速度差时，为曲线运动，两个轮子速度越接近，越趋向直线运动,左轮和右轮在车轴的延长线上J为圆心，车子的其角速度为ω ，因为两个轮子必须保持位置固定，否则就变形了：
（1）当|Vl|>|Vr|，圆运动圆心在车右边（如上图）：
ω=vc/R=vl/(R+L/2)=vr/(R-L/2) 可得：
Vc=ωR
Vl=ω(R+L/2)
Vr=ω*(R-L/2) 进而可得：
Vc=（vl+vr）/2 (1)
ω=(Vl-vr)/L (2)
R=vc/ω=L/2*（vl+vr）/(Vl-vr)，
dθ=ω*Dt
当vr+vl>0，即前右拐,小车方向角减小：
θ(t+dt)=θt-|dθ|
当vr+vl<0,即右退，小车方向角增大：
θ(t+dt)=θt+|dθ|

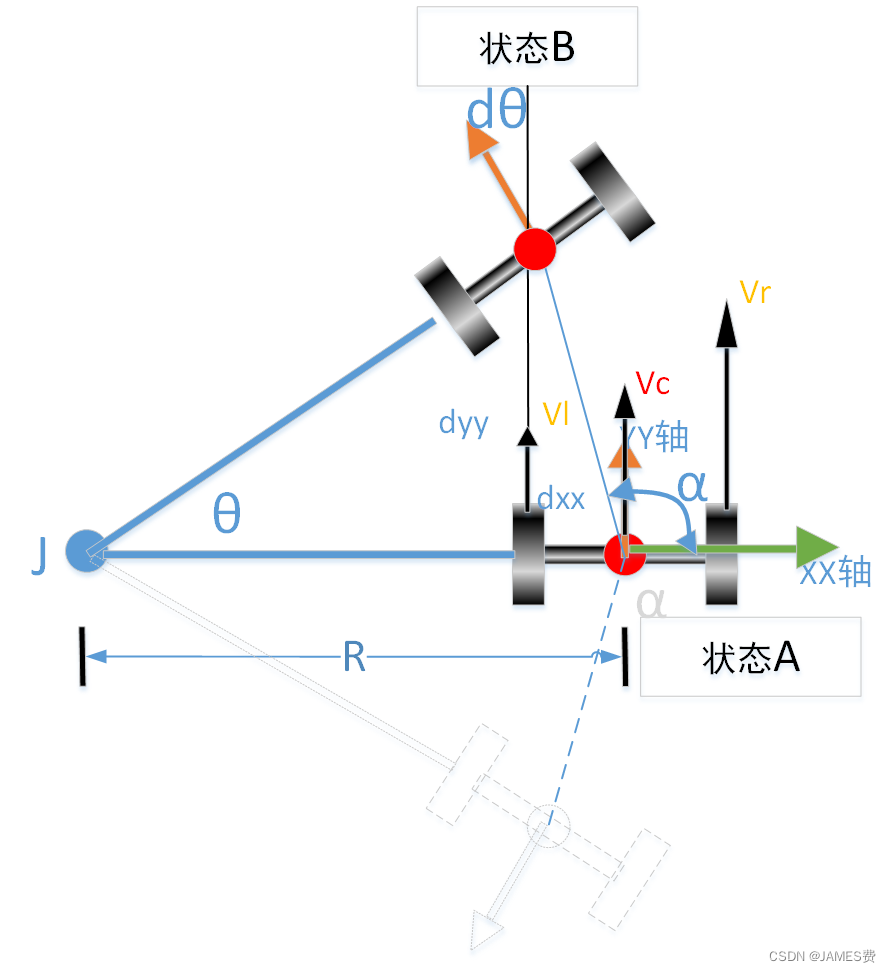
（2）当|Vl|<|Vr|，圆运动圆心在车左边（如上图）,此时逆时针圆周运动为正：
ω=vc/R=vl/(R-L/2)=vr/(R+L/2) 可得：
Vc=ωR
Vl=ω(R-L/2)
Vr=ω*(R+L/2) 进而可得：
Vc=（vl+vr）/2 (1)
ω=(Vr-vl)/L (2)
R=vc/ω=L/2*（vl+vr）/(vr-vl)，
dθ=ω*dt
当vr+vl>0，即前左拐,使小车方向角增大：
θ(t+dt)=θt+|dθ|
当vr+vl<0,即左退，使小车方向角减小：
θ(t+dt)=θt-|dθ|

Step2 获取相对坐标

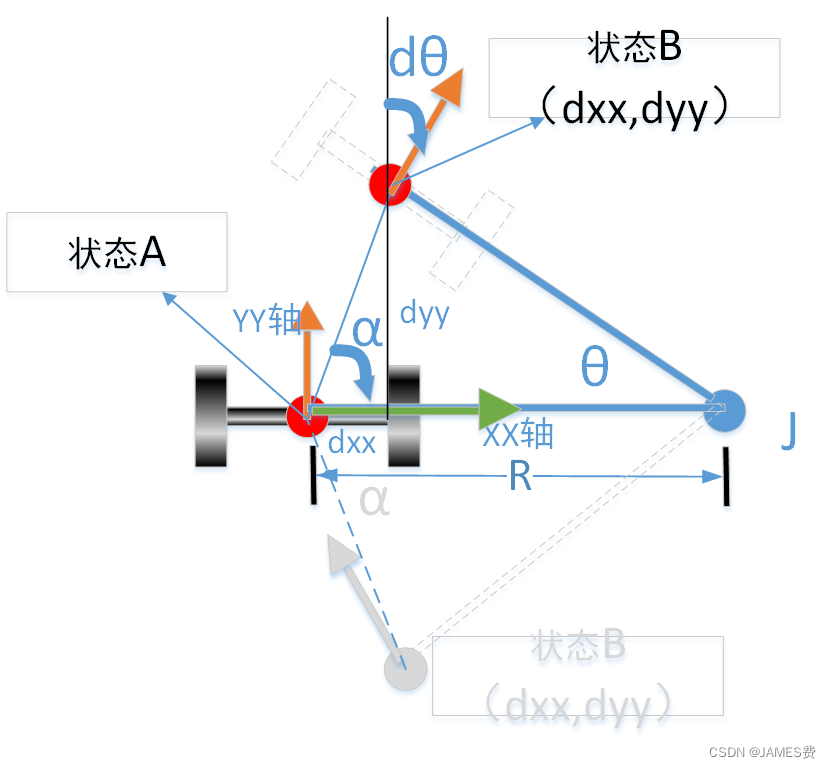
（1）当|Vl|>|Vr|
如图所示，t+dt时刻的状态B，相对于t时刻的小车坐标系上的位置（dxx，dyy），我们可以根据三角形（ABJ）性质及坐标偏移很容易得出：
|AB|=|JA|^2+|JB|2-2cos(θ)|JA||JB|=R*sqrt(2(1-cos(θ)))
当vr+vl>0，即前右拐,B状态点在第一象限：
α =(pi-θ)/2 等腰三角形可得
dxx=|AB|*cos(α)
dyy=|AB|*sin(α)
当vr+vl<0,即右退，B状态点在第四象限：
α=(θ-pi)/2
dxx=|AB|*cos(pi/2+dθ)=|AB|cos(α)
dyy=|AB|sin(pi/2+(pi-θ)/2)=|AB|sin(α)
（2）当|Vl|<|Vr|
|AB|=|JA|^2+|JB|2-2cos(θ)|JA||JB|=Rsqrt(2(1-cos(θ)))
当vr+vl>0，即前右拐,B状态点在第二象限：
α =pi-(pi-θ)/2=(pi+θ)/2
dxx=|AB|*cos(α)
dyy=|AB|*sin(α)
当vr+vl<0,即右退，B状态点在第三象限：
α=-(pi+θ)/2
dxx=|AB|cos(α)
dyy=|AB|sin(α)

Step3 坐标变换，获取大地坐标

上一步计算得到了t+dt时刻状态B的相对坐标（dxx，dyy）
而我们目标是要求状态B的世界坐标，这里我们引入旋转和平移变换的知识：
一个坐标系上一点（x，y），经过坐标系原点逆时针旋转θ后得到的新坐标上的坐标为（x*，y*）则：

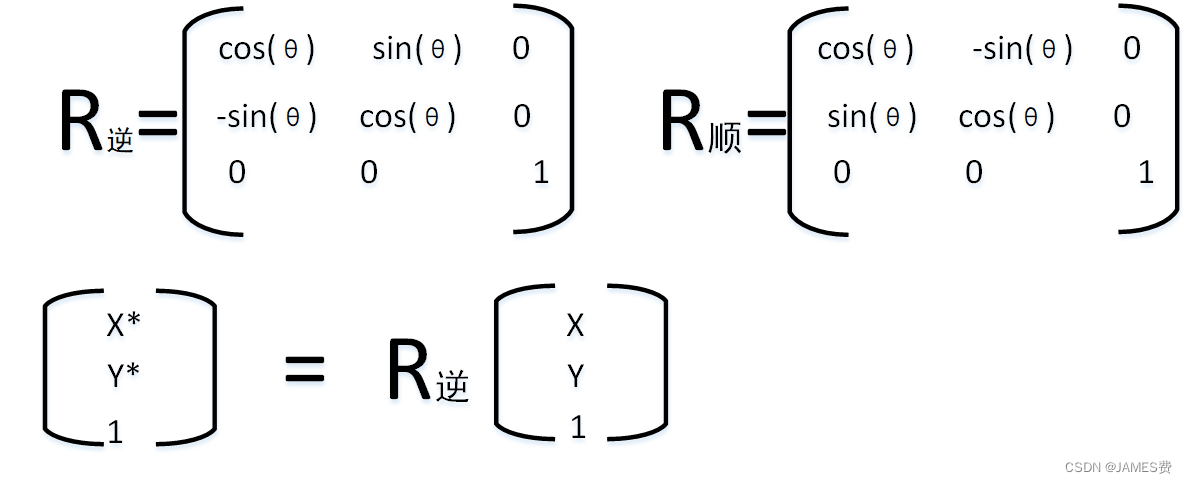
经过坐标系原点顺时针旋转θ后得到的新坐标上的坐标为（x*，y*）则：

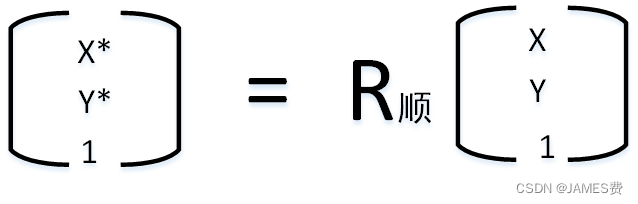
坐标平移也有类似矩阵形式：

求解的问题，我们可以通过先旋转变化到与世界坐标系平行，然后再平移变换，就可得到B状态在世界坐标系的坐标（x_next,y_next）了:

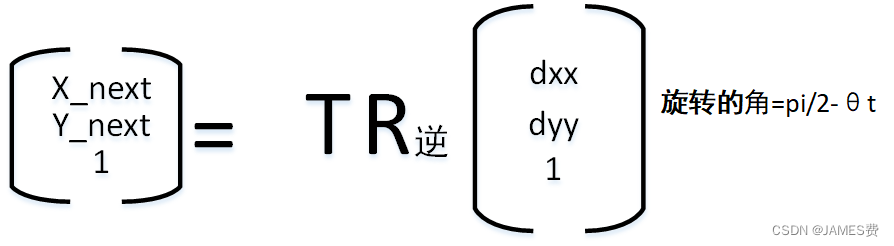
至此小车拐弯的运动正向计算模型就完成了。
此外，小车原地旋转，正向前进后退等，很容易表达，这里就不再赘述。接卸来就可以撸python代码实现了。

3.4 python编程

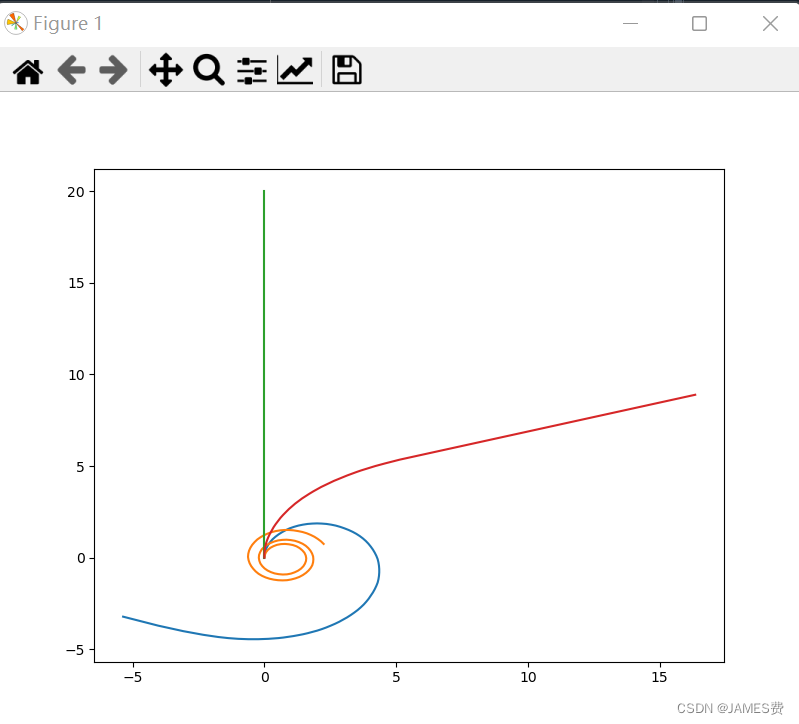
以下为实现小车右转向的核心代码：

def NextState(xt, yt, theta, sl, sr,l=0.5,dt=1,Rw=0.4):
    """
    
    xt,yt： 当前小车机器人位置坐标
    theta: 当前小车机器人方位角,弧度表示
    vl:当前dt，左轮转速值,当为负值为反转
    vr:当前dt,右轮转速值，当为负值为反转
    dt:当前速度持续时间
    l：两个轮子的宽度
    Rw:轮子半径
    return: 返回t+dt时刻的小车位置坐标、朝向
    """
    #小车存在差速的情况，
    vl=sl*2*math.pi*Rw
    vr=sr*2*math.pi*Rw
    print("左右速度：",vl,vr)
    if vl!=vr: 
        if np.abs(vl)>np.abs(vr):  #圆心在右侧情况，圆周运动      
            # 小车的线速度
            vc=(vl+vr)/2
            #小车的角速度
            omiga=(vl-vr)/l
            print("旋转角度：",omiga)
            #小车的圆周运动半径
            R=vc/omiga
            print("圆半径：",R)
            #小车的旋转角增量
            theta_dt=omiga*dt
            
               
            res,line=sovle_lineBy(R,R,theta_dt)
            if res:
                
                #小车下一时刻的方向角 
                if vr+vl>0:#小车右前拐，方向角变小             
                    df=-1
                    
                    alpha=(math.pi-theta_dt)/2
                    
                if vr+vl<0:#小车右后拐，方向角变大 
                    df=1
                    alpha=(theta_dt-math.pi)/2
                    
                print("alpha:",alpha)
                dxx=line*math.cos(alpha)
                dyy=line*math.sin(alpha)
                
                
                theta_next=theta+np.abs(theta_dt)*df    
                #平移矩阵
                T=np.array([[1,0,xt],
                            [0,1,yt],
                            [0,0,1]])
                #旋转矩阵
                Tangle=math.pi/2-theta
                
                R=np.array([[math.cos(Tangle),math.sin(Tangle),0],
                            [-math.sin(Tangle),math.cos(Tangle),0],
                            [0,0,1]])
                XY_t=np.array([[dxx],
                               [dyy],
                               [1]])
                
                xy_next=np.dot(T, np.dot(R,XY_t)) 
                
                x_next=xy_next[0][0]
                y_next=xy_next[1][0]
                print(xy_next)
                print("dxx,dyy",dxx,dyy)
                
            else:
                print("sovle_lineBy failure")
                return False,None,None,None
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

发现,改变左右轮速度，可以玩出无限花样的运动轨迹：

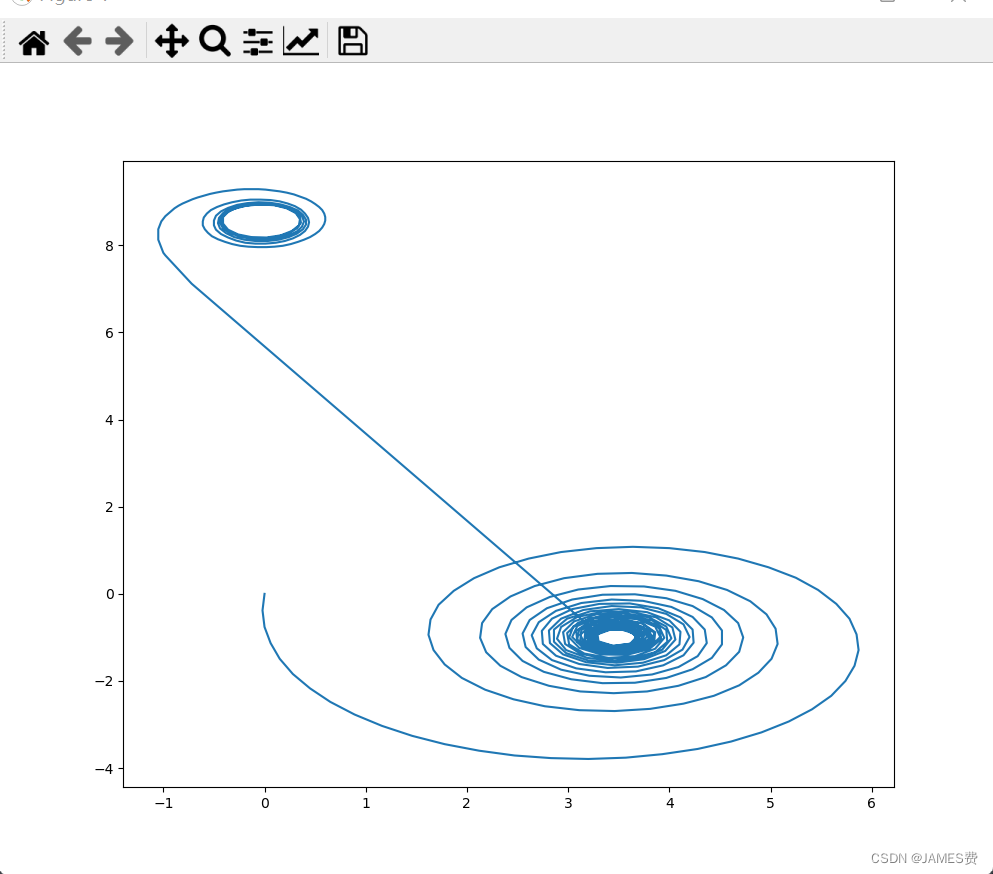
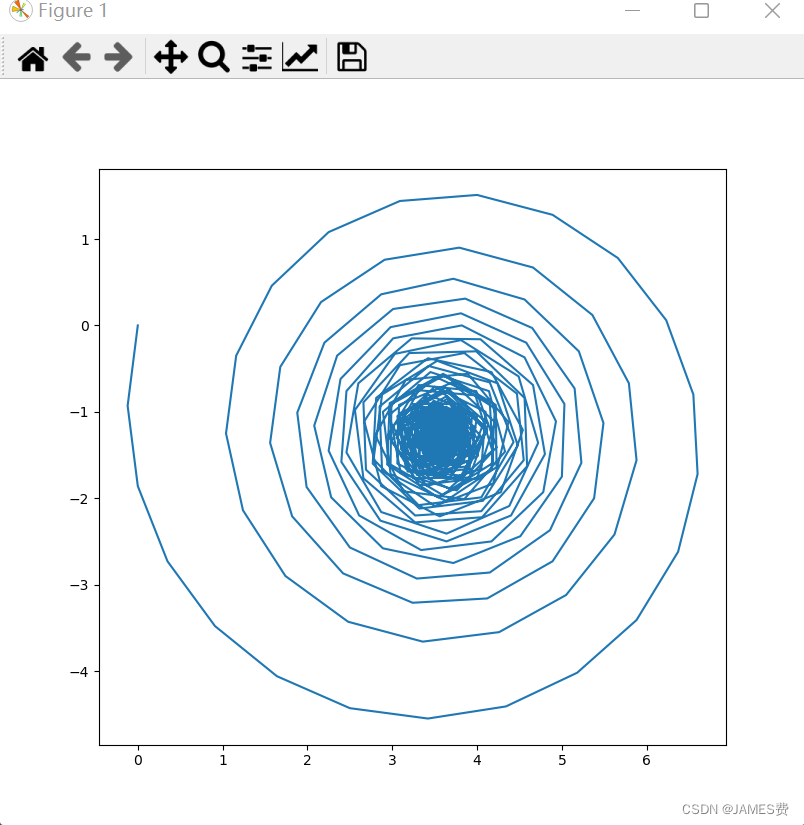
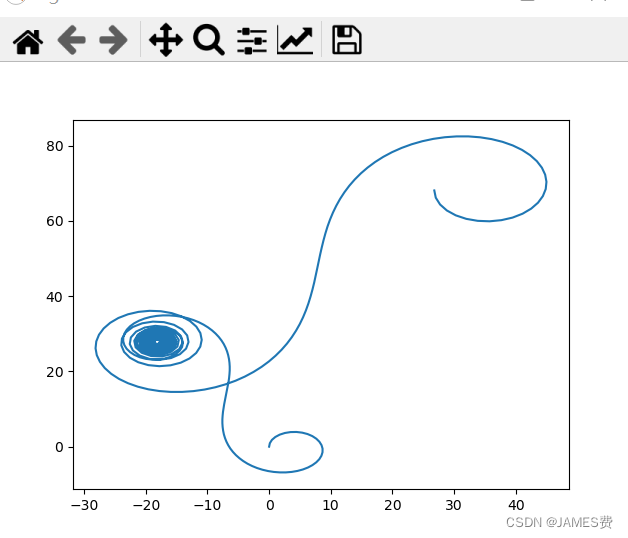
本节完整源码已经上传点击链接

本篇就到此了，接下来我们来研究以下这个小车的逆向控制，叫它指那到哪。