离散数学 ---- 图论基础 --- 图的引入，表示与分类

第一部分 --- 图的引入

一个图是由两部分组成的：1.表示具体事物的点的集合；2.表示事物之间联系的一些线的集合

1.无向图中的所有线都是默认双向的，所以不需要我们标明方向

2.有向图中的所有线都是默认单向的，需要我们标明线的方向

1.两个点之间有两条及以上的线存在的时候称为多重图

2.一个点能够和自己连线的时候（环状线）称为有环图

用数学语言来描述图的时候，节点可以用点的集合来表示，而边则是用两个点的组合来表示

其中边分为两种，一种是有序表（有方向的边），一种是无序边（没有方向的边），对于有序边，我们可以用笛卡尔积和序偶来表示，而对于无序边我们则定义了无序对和无序积来表示

---

第二部分 --- 图的表示

在边的集合中元素有两种类型：1.无序结点对；2.有序节点对

1.同一个图可以有不同的邻接矩阵来描述，但是由于这些不同的邻接矩阵描述的都是同一个图，所以我们忽视掉这些邻接矩阵的不同，取其中一个邻接矩阵来代表这个图剩下的所有邻接矩阵

 

---

 第三部分 --- 图的分类

1.两个结点间的一条无向边同时指向两个结点，可以实现信息在两个结点间的相互传递

2.根据1的特性我们可以将两个结点A，B之间的一条无向边拆分为两条有向边，一条有向边从A指向B，一条有向边从B指向A

3.遇到混合图时，我们常常将混合图中的无向边根据2中的特性转换为有向边，将混合图转化为有向图来分析

1.注意在有向图中的平行边的定义是：两结点间同起点，同终点，也就是说有向图中的平行边是分方向的，两个结点间同方向上的多条边才能称为平行边

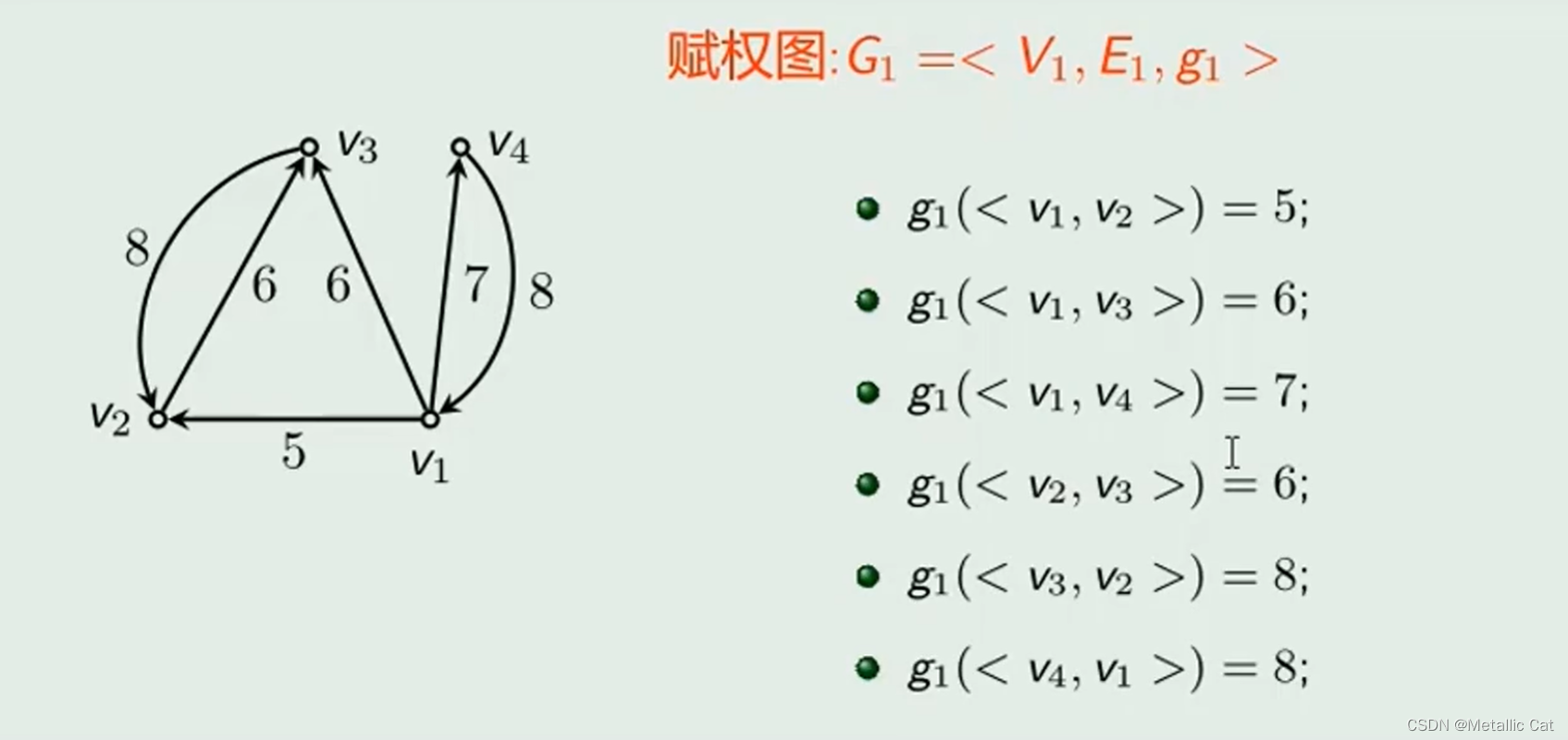
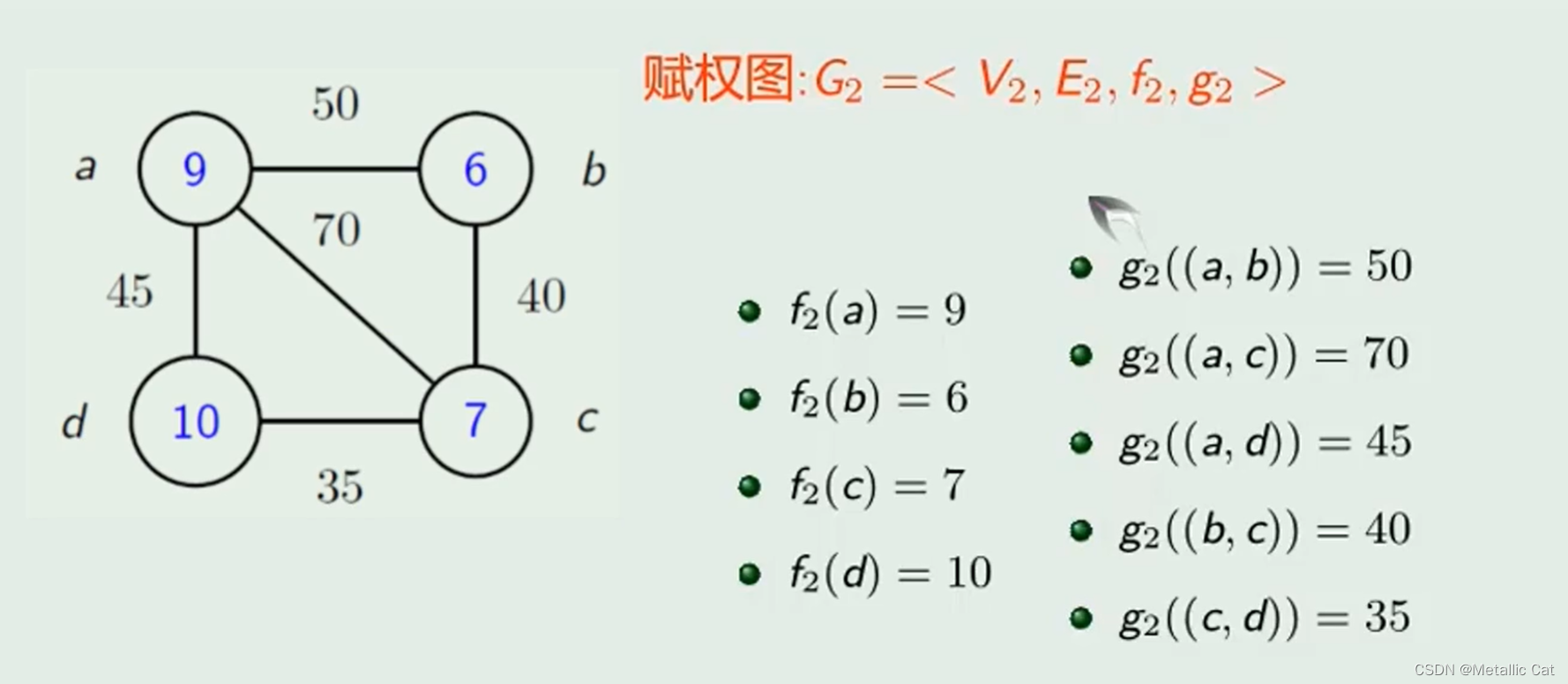
有时除了考虑两个结点间是否有边之外还要考虑两个结点间的边的强度问题