-
【图像处理】德里奇( Deriche)边缘检测器
一、提要
Deriche边缘检测,同canny算法齐名,因此,知道canny原理,也有必要知道德里奇的检测原理。本篇专门针对德里奇算法展开讨论。
二、图像预处理
2.1 Gauss 滤波
由于所有边缘检测结果都很有可能受到噪音影响,去除噪音防止错误检测是基本的任务。为了光滑图像,可以用 Gauss 滤波与图像卷积。这个过程可以轻微地光滑图像,去除明显的噪音。内核大小为 ( 2 k + 1 ) × ( 2 k + 1 ) 的 Gauss 内核的方程为:
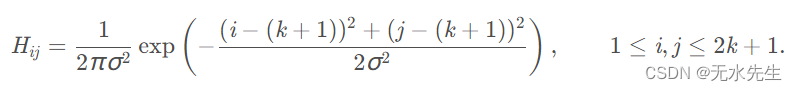
这里给出一个 5 × 5 Gauss 滤波的例子,用于建立相邻图像,σ = 1.4 。(星号表示卷积操作)

我们需要知道 Gauss 核的大小会影响检测的性能。尺寸越大,对噪音的敏感性越弱。此外,检测边缘的局部误差会随着 Gauss 核尺寸的增加而增加。5 × 5 对大多数情形是一个好的选择,但也可以根据特殊的情况变化。
三、 Deriche 边缘检测器
Deriche边缘检测器是Rachid Deriche在1987年开发的一种边缘检测算子,它是一种多步算法,用于在离散的二维图像中获得边缘检测的最优结果。边缘检测(Canny's edge detection)及其最优边缘标准检测:
- 检测质量——应标记所有现有边缘,并且不应发生错误检测。
- 准确性 - 标记的边缘应尽可能接近真实图像中的边缘。
- 明确性 - 图像中的给定边缘应仅标记一次。对真实图像中的一个边缘不应发生多次响应。
因此,该算法通常被称为 Canny-Derich 检测器。
Deriche 边缘检测器和 Canny 边缘检测器一样,由以下 4 个步骤组成:
- 图像平滑
- 计算幅度和梯度方向
- 非最大抑制
- 滞后阈值(使用两个阈值)
本质区别在于算法前两步的实现,与Canny边缘检测器不同,Deriche边缘检测器使用IIR滤波器,形式为:
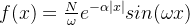
该过滤器对 Canny 准则进行了优化,从前面的公式可以看出,当
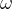 的值接近 0 时,得到最有效的过滤器。这样的过滤器使用公式:
的值接近 0 时,得到最有效的过滤器。这样的过滤器使用公式: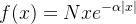
这种滤波器的优点是只用一个参数就可以适应处理后图像的特征,如果α值很小(通常在0.25到0.5之间),检测效果更好。该参数具有更高的值(大约 2 或 3)。

使用 IIR 滤波器是有意义的,特别是在处理后的图像有噪声或需要大量平滑的情况下(这导致 FIR 滤波器的卷积核很大)。因为它能够在独立于所需的平滑量。
四、Deriche 检测器实现细节
可以将获取二维Deriche滤波器的值的过程分为两个部分。在第一部分中,图像数组根据以下公式在水平方向上从左向右传递:
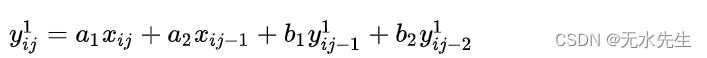
并根据公式从右到左:
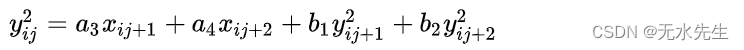
然后将计算结果存储到临时二维数组中:
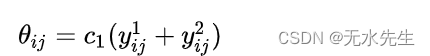
该算法的第二步与第一步非常相似。上一步中的二维数组用作输入。然后根据以下公式在垂直方向上从上到下以及自下而上传递:
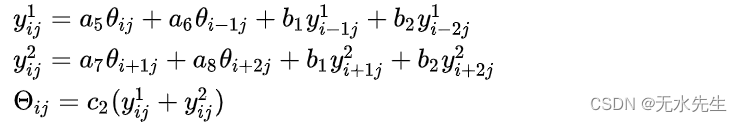
该算法的描述意味着处理后的行和列是相互独立的。因此,基于IIR滤波器的解决方案通常用于支持高级并行化的嵌入式系统和架构中。
参数表:
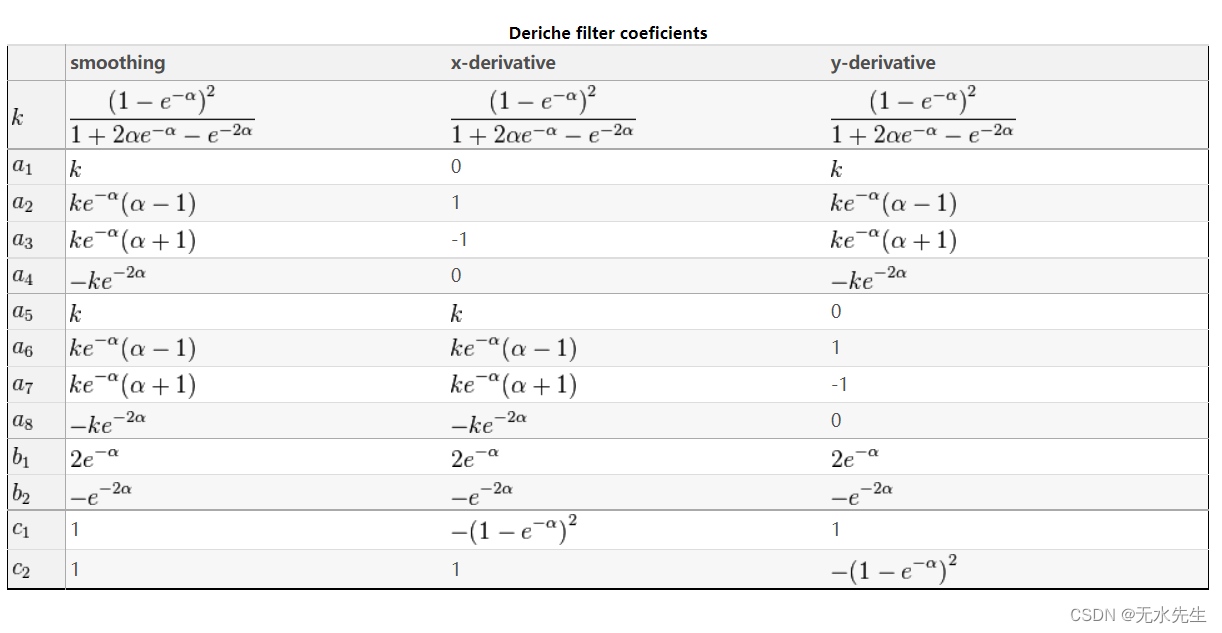
-
相关阅读:
Java基础面试高频问题总结(二)
Docker入门
Linux安装Tomcat并且设置开机自启动
猿创征文|从JAVAER到GISER的进击之路
Flutter学习-开篇
保证接口数据安全的10种方案
ssm+vue+elementUI 医院门诊互联电子病历管理信息系统-#毕业设计
Java面试题:并发编程高频面试题,请你说一下你对Happens-Before的理解
Network Address Translation,网络地址转换技术
LeetCode第53题:最大子数组和【python 5种算法】
- 原文地址:https://blog.csdn.net/gongdiwudu/article/details/126723153