插入排序、希尔排序

目录

插入排序

希尔排序

---

插入排序

 插入排序就像我们打扑克摸牌理顺的过程一样，将后面的牌一张一张按大小（升降序）排列好。

 插入排序也就是这么个过程，这里假设排升序，步骤：

1、先实现单次的插入过程，先取末尾的数（先不初始化值），下标记为end，找他后面一个数（下标为end+1），用一个临时变量tmp记录，比较这两个数，如果前面>后面，就把前面的数往后挪一位，--end。

2、重复上述过程，直到end < 0 为止，显然这是一个循环的过程，条件就是end >= 0，如果前面 < 后面，就break出来。这时再将tmp放到end+1的位置就完成了单次的插排。

3、单次的完成，在外面套一个循环就可以实现整个插入排序了，这时也能确定end的初始值。

 

代码如下：

void Insertsort(int* a, int n)
{
	//将下标为end+1的数 插入到[0,end]里面，并保证有序
	for (int i = 0; i < n - 1; ++i)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + 1] = a[end];
				--end;
			}
			else
				break;
		}
		a[end + 1] = tmp;
	}
}
int main()
{
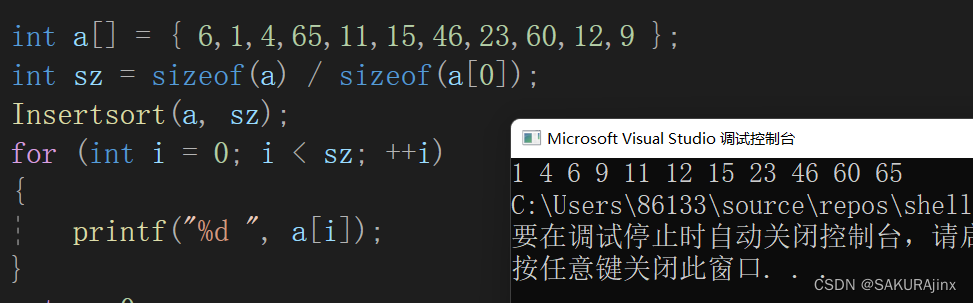
	int a[] = { 6,1,4,65,11,15,46,23,60,12,9 };
	int sz = sizeof(a) / sizeof(a[0]);
	Insertsort(a, sz);
	for (int i = 0; i < sz; ++i)
	{
		printf("%d ", a[i]);
	}
	return 0;
}

希尔排序

希尔排序实质上就是插入排序的深度优化，但是它的效率一下就提升到和堆排这种时间复杂度为O(N*logN)差不多的级别了。

那希尔排序是如何实现优化的呢？实际上它在插入排序之前进行了预排序，目的是让序列更接近有序。

 这里定义一个gap，假设gap = 3，将降序序列{9,8,7,6,5,4,3,2,1,0} 按间隔为gap的 为一组进行插入排序，如9,6,3,0为一组，8,5,2为一组，7,4,1为一组，分成这样的三组插入排序，排完后序列变成{0,2,1,3,5,4,6,8,7,9} 将小的基本放在了前面，将大的基本放在了后面，实现了基本的有序，这就为最后一次的排序做了铺垫，这就是预排序。

很多人会问，预排序不也是插入排序吗，为什么进行多次预排序反而比一次直接插入排序效率高呢？这就是gap的妙处了，如果是插入排序，需要从头到尾依次挪动数据，如果不巧可能最后一个数要一直往前插入到最前面。   先进行预排序的话，能先大致处理序列的有序性，基本避免了最坏的情况，能节省很多时间。

我们来尝试实现一下希尔排序

还是和插入排序一样，先实现单次的排序。

        int end;
		int tmp = a[end + gap];
		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + gap] = a[end];
				end -= gap;
			}
			else
				break;
		}
		a[end + gap] = tmp;

单次的希尔排序就完成了，实际上就是插入排序就是gap = 1 的情况。

来看整体的：

预排后就是gap组多组并排，这里有两种写法:

一、  三层循环

int gap = 3;
	for (int j = 0; j < gap; ++j)
	{
		for (int i = j; i < n - gap; i+= gap)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
					break;
			}
			a[end + gap] = tmp;
		}
	}
	
}

这种就是按上面的图一组一组分别排序每个gap组的数据。

先排9,6,3,0这一组，再排8,5,2这一组，再排7,4,1这一组。分别排序，排完一组再排下一组。

二、两层循环

	int gap = 3;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
					break;
			}
			a[end + gap] = tmp;
		}
	}

这种是改进过的，看上去更简便一些。与上面一种排序顺序不同，它是依次顺着序列往下走的。

先排第一个数，9,6排一下； 再排第二个数，8,5排一下； 再排第三个数，7,4排一下。

它是依次往下排的，结果来说也是一样的。

最外层：到这 希尔排序还差最外层调整gap

按上面情况分析，gap越大，跳的越快，但是相对可能没那么有序。

                             gap越小，跳的越慢，但是更接近有序。

所以说，gap = 1 时也就是直接插入排序了。

因此，我们用数组个数n来控制gap，让它实现多组排序。

void Shellsort(int* a, int n)
{
		int gap = n;
		while (gap > 1)
		{
			gap = gap / 3 + 1;
			for (int i = 0; i < n - gap; i++)
			{
				int end = i;
				int tmp = a[end + gap];
				//将下标为end+gap的数 插入到[0,end]里面，并保证有序
				while (end >= 0)
				{
					if (a[end] > tmp)
					{
						a[end + gap] = a[end];
						end -= gap;
					}
					else
						break;
				}
				a[end + gap] = tmp;
			}
		}
}

当gap > 1时，就是预排序，当gap = 1时，进行最后一次直接插入排序。

这里gap / 3+1 是为了保证gap最后一次 == 1进入，当然gap / 2也是可以的，但是经过测试还是/3效率更高一点。

希尔排序时间复杂度大概是O(N^1.3)，这是个大概的测试估值，算是比较官方的数据了，要计算它的时间复杂度需要很深的数学功底了。