Imaging through Atmospheric Turbulence笔记（二）

0. 前言

用傅里叶光学描述下幅图片：

• 空间变模糊
• 像素的变化
• 随着距离的变化
• 振幅还可以

平常观察到清晰的图片 vs 大气湍流

1. 清晰图片（通过真空传播）

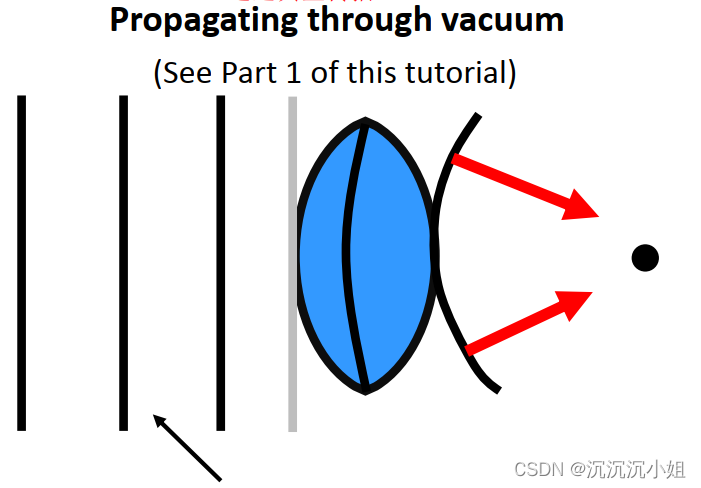
• 没有随机性
• 无折射率变化
• 波的相位不失真

2. 模糊图片（通过大气湍流传播）

•  折射率的变化
• 变化是随机的
• 有些点会延迟/提前
• 这是通过波的相位实现的
• 因此，失真=相位变化

1. 折射率（Index of refraction）

折射率是相位畸变的来源。

折射率由以下公式组成：

其中：

• r 为3D坐标，也就是位置
• t 为时间
• λ 为波长
•  mean index（平均指数）是一个常数
• fluctuation（波动）是随机的，这就是湍流效应发挥作用的地方。
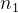•  对波长的依赖性相对较弱，特别是当我们讨论可见波段时。

其中fluctuation是随机的过程，它的随机情况其自相关函数决定，其自相关函数如下：

若自相关是齐次的（即广义平稳），则可以使用傅里叶变换进行处理。否则，任何信号处理都是一场噩梦。 

2. 功率谱密度（PSD）

定义：在物理学中，信号通常是波的形式表示，例如电磁波、随机振动或声波。当波的功率频谱密度乘以一个适当的系数后将得到每单位频率携带的功率，这称为信号的功率谱密度（power spectral density， PSD）。

功率谱密度（PSD），它定义了信号或者时间序列的功率如何随频率分布。这里功率可能是实际物理上的功率，或者更经常便于表示抽象的信号被定义为信号数值的平方，也就是当信号的负载为1欧姆（ohm）时的实际功率。此时瞬间功率（平均功率的中间值）可表示为：

由于平均值不为零的信号不是平方可积，所以在这种情况下就没有傅里叶变换。幸运的是维纳-辛钦定理（Wiener Khinchin theorem）提供了一个简单的替换方法，如果信号可以看作是平稳的随机过程，那么功率谱密度就是信号自相关函数的傅里叶变换。

当存在自相关函数时，也可以定义功率谱密度。对于齐次随机过程，功率谱密度是自相关函数的傅里叶变换。 

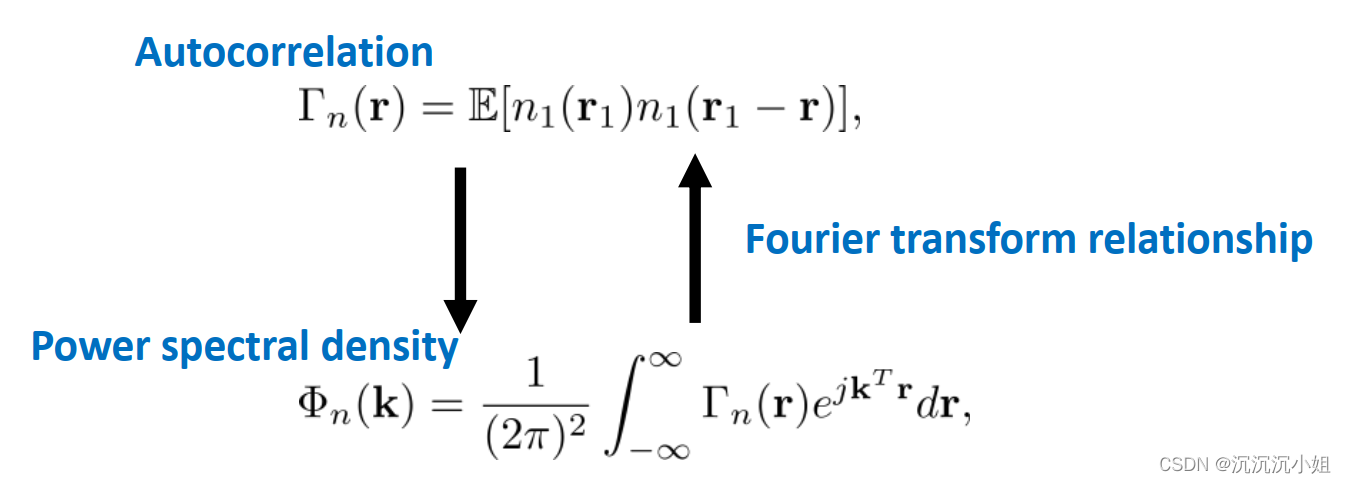
功率谱密度公式：

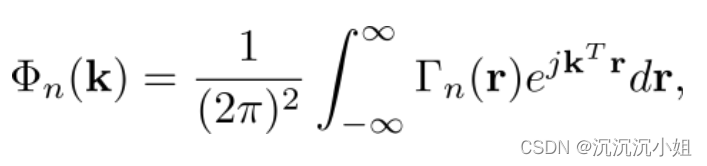
其中Kolmogorov功率谱公式和Von Karman频率普公式如下所示：

 

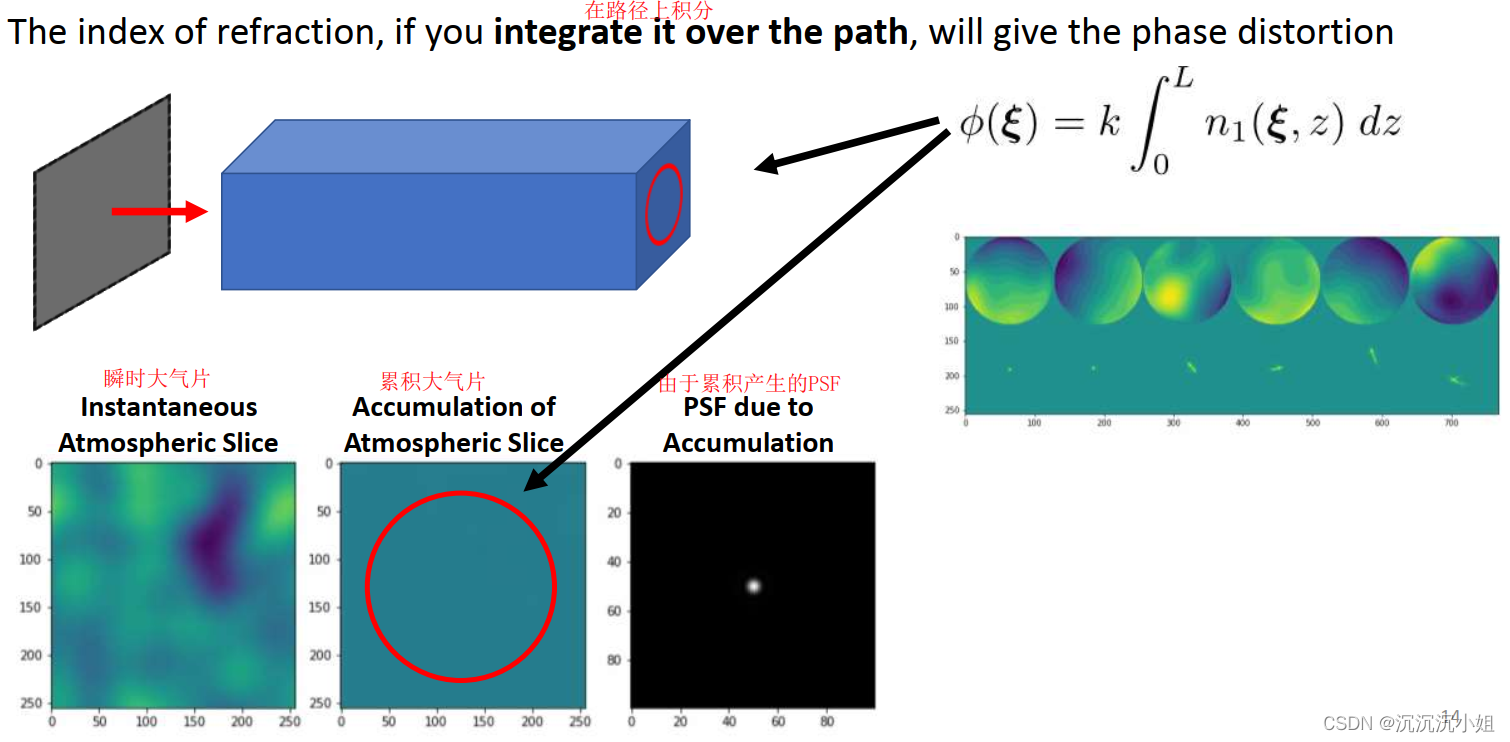
3. 观察波如何被湍流影响的：

在衍射路径上积分，将会获得相位畸变。

4. 生成随机领域

有很多方法，但此处仅关注使用傅里叶基础的方法：

1. 协方差/输入PSD
2. 白噪声(White noise)
3. 输出的随机领域：output field = Fourier^-^1\left \{ \sqrt{PSD}\otimes Fourier(whitenoise) \right \}" role="presentation" style="position: relative;">output field = Fourier^-^1\left \{ \sqrt{PSD}\otimes Fourier(whitenoise) \right \}$\text{output field = Fourier^-^1left { sqrt{PSD}otimes Fourier(whitenoise) right }}$