-
灰色预测模型
特点
- 使用的数据是将原始数据通过累加生成(或其他方式生成)得到近似指规律的数据序列。
- 优点:
- 对数据量要求不高,一般只需要4个数据;
- 解决了历史数据少、序列的完整性及可靠性低的问题;
- 能利用微分防尘来充分挖掘系统的本质,精度高;
- 将无规律的原始数据进行生成的到规律性较强的生成序列,易于检验,不考虑分布规律和变化趋势;
- 缺点:
- 之适用于中短期的预测,只适合指数增长的预测;
GM(1, 1) 预测模型
GM(1, 1)表示模型是一阶微分方程,且只含1个变量的灰色模型。
相关定义:
原始数据序列: x ( 0 ) = ( x ( 0 ) ( 1 ) , x ( 0 ) ( 2 ) , … , x ( 0 ) ( n ) ) x^{(0)}=(x^{(0)}(1), x^{(0)}(2),\dots,x^{(0)}(n)) x(0)=(x(0)(1),x(0)(2),…,x(0)(n))
级比: λ ( k ) = x ( 0 ) ( k − 1 ) x ( 0 ) ( k ) , k = 2 , … , n \lambda(k)=\frac{x^{(0)}(k-1)}{x^{(0)}(k)},k=2,\dots,n λ(k)=x(0)(k)x(0)(k−1),k=2,…,n,如果所有的级比 λ ( k ) \lambda(k) λ(k)都落在可覆盖范围 Θ = ( e − 2 n + 1 , e 2 n + 2 ) \Theta=(e^{-\frac{2}{n+1}},e^{\frac{2}{n+2}}) Θ=(e−n+12,en+22)内,则说明序列 x ( 0 ) x^{(0)} x(0)可使用GM(1,1)模型进行灰色预测;否则需要对序列 x ( 0 ) x^{(0)} x(0)进行变换处理,使其落在可覆盖范围内(即去适当的常数 c c c,进行平移变换), y ( 0 ) ( k ) = x ( 0 ) ( k ) + c , k = 1 , … , n y^{(0)}(k)=x^{(0)}(k)+c,k=1,\dots,n y(0)(k)=x(0)(k)+c,k=1,…,n,然后对 y ( 0 ) y^{(0)} y(0)进行GM(1,1)灰色预测。
一次累加生成序列: x ( 1 ) x^{(1)} x(1)( x ( 0 ) x^{(0)} x(0)的1-AGO序列)
x ( 1 ) = ( x ( 1 ) ( 1 ) , x ( 1 ) ( 2 ) , … , x ( 1 ) ( n ) ) = ( x ( 0 ) ( 1 ) , x ( 0 ) ( 2 ) + x ( 0 ) ( 2 ) , … , ∑ i = 0 n x ( 0 ) ( i ) ) x(1)=(x(1)(1),x(1)(2),…,x(1)(n))=(x(0)(1),x(0)(2)+x(0)(2),…,n∑i=0x(0)(i)) x(1)=(x(1)(1),x(1)(2),…,x(1)(n))=(x(0)(1),x(0)(2)+x(0)(2),…,i=0∑nx(0)(i))
x ( 1 ) x^{(1)} x(1)中紧邻两个值的均值序列:
z ( 1 ) = ( z ( 1 ) ( 2 ) , z ( 1 ) ( 3 ) , … , z ( 1 ) ( n ) ) , 其中 z ( 1 ) ( k ) = 1 2 ( x ( 1 ) ( k ) + x ( 1 ) ( k − 1 ) ) , k = 2 , … , n z^{(1)}=(z^{(1)}(2), z^{(1)}(3),\dots,z^{(1)}(n)), 其中z^{(1)}(k)=\frac{1}{2}(x^{(1)}(k)+x^{(1)}(k-1)),k=2,\dots,n z(1)=(z(1)(2),z(1)(3),…,z(1)(n)),其中z(1)(k)=21(x(1)(k)+x(1)(k−1)),k=2,…,n
我们称 x ( 0 ) ( k ) + a z ( 1 ) ( k ) = b , 其中 k = 2 , … , n x^{(0)}(k)+az^{(1)}(k)=b, 其中k=2,\dots,n x(0)(k)+az(1)(k)=b,其中k=2,…,n为GM(1,1)模型的基本形式,其中 b b b表示灰作用量, − a -a −a表示发展系数。
记 u = [ a , b ] T , Y = [ x ( 0 ) ( 2 ) , … , x ( 0 ) ( n ) ] T , B = [ − z ( 1 ) ( 2 ) 1 ⋮ ⋮ − z ( 1 ) ( n ) 1 ] \mathbf{u}=[a,b]^T,\mathbf{Y}=[x^{(0)}(2),\dots,x^{(0)}(n)]^T,\mathbf{B}=\left[−z(1)(2)1⋮⋮−z(1)(n)1\right] u=[a,b]T,Y=[x(0)(2),…,x(0)(n)]T,B=⎣ ⎡−z(1)(2)⋮−z(1)(n)1⋮1⎦ ⎤,于是 x ( 0 ) ( k ) + a z ( 1 ) ( k ) = b x^{(0)}(k)+az^{(1)}(k)=b x(0)(k)+az(1)(k)=b可以表示为
Y = B u \mathbf{Y}=\mathbf{Bu} Y=Bu
设目标函数为 J ( u ) = ( Y − B u ) T ( Y − B u ) \mathbf{J(u)}=\mathbf{(Y-Bu)}^T\mathbf{(Y-Bu)} J(u)=(Y−Bu)T(Y−Bu),由最小二乘法求得使目标函数取得最小值时 u \mathbf{u} u的估计值为
u ^ = [ a ^ , b ^ ] T = ( B T B ) − 1 B T Y \mathbf{\hat u}=[\hat a,\hat b]^T=(\mathbf{B}^T\mathbf{B})^{-1}\mathbf{B}^T\mathbf{Y} u^=[a^,b^]T=(BTB)−1BTY
白化方程:
由上可得到: x ( 0 ) ( k ) = − a ^ z ( 1 ) ( k ) + b ^ , k = 2 , … , n x^{(0)}(k)=-\hat az^{(1)}(k)+\hat b,k=2,\dots,n x(0)(k)=−a^z(1)(k)+b^,k=2,…,n。
x ( 0 ) ( k ) = x ( 1 ) ( k ) − x ( 1 ) ( k − 1 ) = ∫ k − 1 k d x ( 1 ) ( t ) d t d t x^{(0)}(k)=x^{(1)}(k)-x^{(1)}(k-1)=\int_{k-1}^k\frac{dx^{(1)}(t)}{dt}dt x(0)(k)=x(1)(k)−x(1)(k−1)=∫k−1kdtdx(1)(t)dt(牛顿-莱布尼茨公式)
z ( 1 ) ( k ) = 1 2 ( x ( 1 ) ( k ) + x ( 1 ) ( k − 1 ) ) ≈ ∫ k − 1 k x ( 1 ) ( t ) d t z^{(1)}(k)=\frac{1}{2}(x^{(1)}(k)+x^{(1)}(k-1))\approx\int_{k-1}^kx^{(1)}(t)dt z(1)(k)=21(x(1)(k)+x(1)(k−1))≈∫k−1kx(1)(t)dt(定积分的几何意义, x k ( 1 ) 到 x k − 1 ( 1 ) x^{(1)}_k到x^{(1)}_{k-1} xk(1)到xk−1(1)与 t t t轴围成的面积相等)
因此有:
∫ k − 1 k d x ( 1 ) ( t ) d t d t ≈ − a ^ ∫ k − 1 k x ( 1 ) ( t ) d t + ∫ k − 1 k b ^ d t = ∫ k − 1 k [ − a ^ x ( 1 ) ( t ) + b ^ ] d t ∫kk−1dx(1)(t)dtdt≈−ˆa∫kk−1x(1)(t)dt+∫kk−1ˆbdt=∫kk−1[−ˆax(1)(t)+ˆb]dt ∫k−1kdtdx(1)(t)dt≈−a^∫k−1kx(1)(t)dt+∫k−1kb^dt=∫k−1k[−a^x(1)(t)+b^]dt
于是,得到微分方程: d x ( 1 ) ( t ) d t = − a ^ x ( 1 ) ( t ) + b ^ \frac{dx^{(1)}(t)}{dt}=-\hat a x^{(1)}(t) + \hat b dtdx(1)(t)=−a^x(1)(t)+b^ 被称为GM(1,1)模型的白化方程。
由上面的微分方程,最终可以得到:
x ^ ( 1 ) ( k + 1 ) = ( x ( 0 ) ( 1 ) − b ^ a ^ ) e − a ^ k + b ^ a ^ , k = 0 , 1 , … \hat x^{(1)}(k+1)=\left(x^{(0)}(1) - \frac{\hat b}{\hat a}\right)e^{-\hat a k}+ \frac{\hat b}{\hat a},k=0,1,\dots x^(1)(k+1)=(x(0)(1)−a^b^)e−a^k+a^b^,k=0,1,…检验预测值
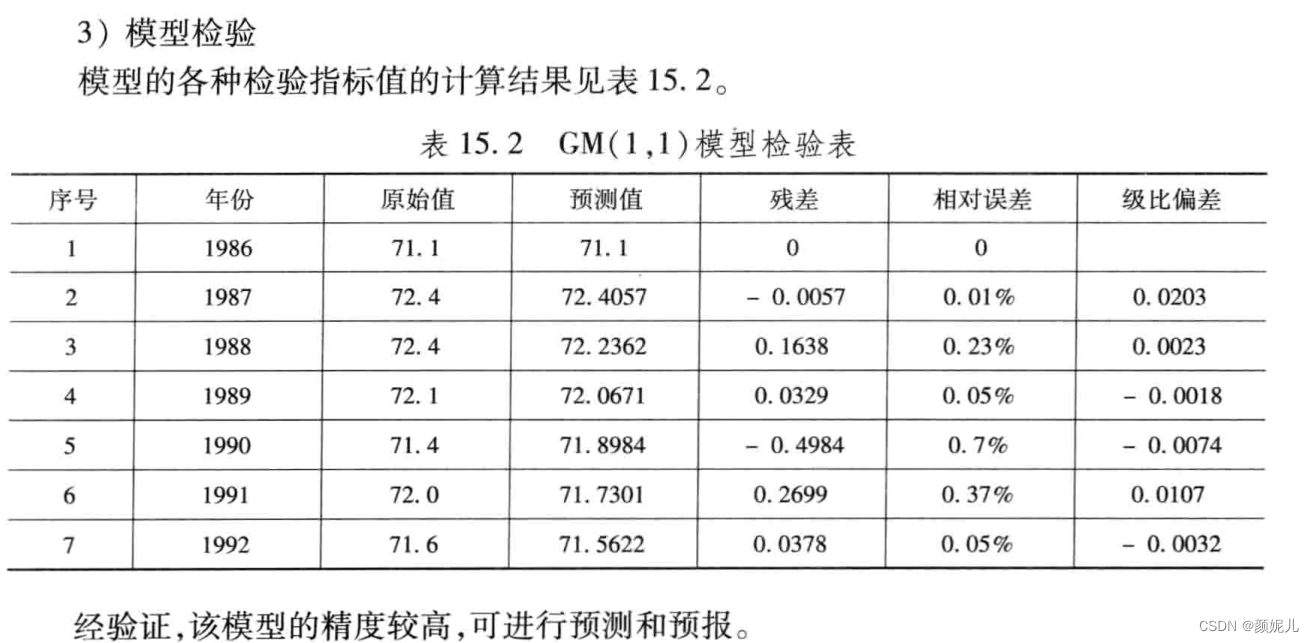
(1)残差检验。令残差为 ε ( k ) \varepsilon(k) ε(k), ε ( k ) = x ( 0 ) ( k ) − x ^ ( 0 ) ( k ) x ( 0 ) ( k ) , k = 1 , … , n \varepsilon(k)=\frac{x^{(0)}(k) - \hat x^{(0)}(k)}{x^{(0)}(k)},k=1,\dots,n ε(k)=x(0)(k)x(0)(k)−x^(0)(k),k=1,…,n
如果 ε ( k ) < 0.2 \varepsilon(k) < 0.2 ε(k)<0.2,则可认为达到一般要求;若 ε ( k ) < 0.1 \varepsilon(k) < 0.1 ε(k)<0.1,则可认为达到较高要求。
(2)级比偏差值检验。令级比偏差为 ρ ( k ) \rho(k) ρ(k), ρ ( k ) = 1 − 1 − 0.5 a 1 + 0.5 a λ ( k ) , k = 1 , … , n \rho(k)=1 - \frac{1- 0.5a}{1+ 0.5a}\lambda (k),k=1,\dots,n ρ(k)=1−1+0.5a1−0.5aλ(k),k=1,…,n
如果 ρ ( k ) < 0.2 \rho(k) < 0.2 ρ(k)<0.2,则可认为达到一般要求;若 ρ ( k ) < 0.1 \rho(k) < 0.1 ρ(k)<0.1,则可认为达到较高要求。案例
结合案例能更好理解(偷个懒啦):



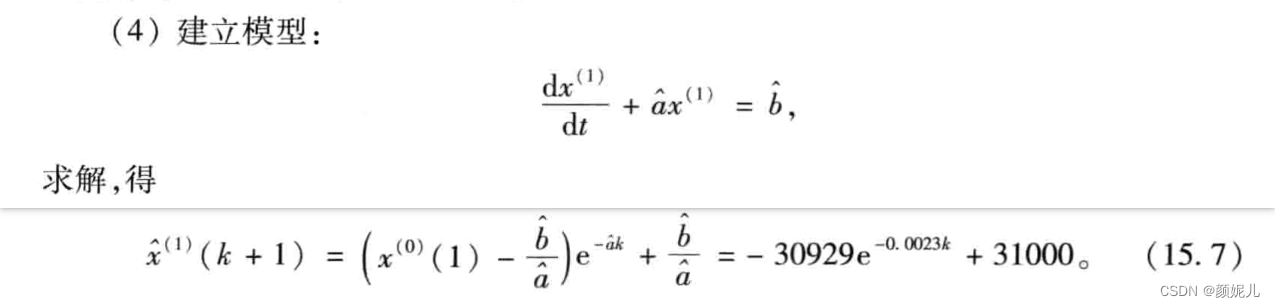

Matlab代码

GM(1,1)适用于具有较强指数规律的序列,只能描述单调变化过程,对于非单调的摆动发展序列或有饱和的S形序列,可以考虑使用GM(2,1)、DGM和Verhulst模型。GM(2,1)
GM(2,1)相较GM(1,1)而言,多了一次累减生成序列,用 α ( 1 ) x ( 0 ) \alpha^{(1)}x^{(0)} α(1)x(0)表示( x ( 0 ) x^{(0)} x(0)的(1-IAGO)序列)。
α ( 1 ) x ( 0 ) = ( α ( 1 ) x ( 0 ) ( 2 ) , … , α ( 1 ) x ( 0 ) ( n ) ) \alpha^{(1)}x^{(0)} = (\alpha^{(1)}x^{(0)}(2),\dots,\alpha^{(1)}x^{(0)}(n)) α(1)x(0)=(α(1)x(0)(2),…,α(1)x(0)(n)),其中
α ( 1 ) x ( 0 ) ( k ) = x ( 0 ) ( k ) − x ( 0 ) ( k − 1 ) , k = 2 , … n \alpha^{(1)}x^{(0)}(k)=x^{(0)}(k)-x^{(0)}(k-1),k=2,\dots n α(1)x(0)(k)=x(0)(k)−x(0)(k−1),k=2,…n
GM(2,1)基本模型为:
α ( 1 ) x ( 0 ) ( k ) + a 1 x ( 0 ) ( k ) + a 2 z ( 1 ) ( k ) = b \alpha^{(1)}x^{(0)}(k)+a_1x^{(0)}(k)+a_2z^{(1)}(k) = b α(1)x(0)(k)+a1x(0)(k)+a2z(1)(k)=b
其白化方程为:
d 2 x ( 1 ) d t 2 + a 1 d x ( 1 ) d t + a 2 x ( 1 ) = b \frac{d^2x^{(1)}}{dt^2}+a_1\frac{dx^{(1)}}{dt}+a_2x^{(1)}=b dt2d2x(1)+a1dtdx(1)+a2x(1)=b
令 u = [ a 1 , a 2 , b ] T , Y = [ α ( 1 ) x ( 0 ) ( 2 ) , α ( 1 ) x ( 0 ) ( 3 ) , … , α ( 1 ) x ( 0 ) ( n ) ] T = [ x ( 0 ) ( 2 ) − x ( 0 ) ( 1 ) , [ x ( 0 ) ( 3 ) − x ( 0 ) ( 2 ) , … , x ( 0 ) ( n ) − x ( 0 ) ( n − 1 ) ] T , B = [ − x ( 0 ) ( 2 ) − z ( 1 ) ( 2 ) 1 ⋮ ⋮ ⋮ − x ( 0 ) ( n ) − z ( 1 ) ( n ) 1 ] \mathbf{u}=[a_1,a_2,b]^T, \mathbf{Y}=[\alpha ^{(1)}x^{(0)}(2), \alpha ^{(1)}x^{(0)}(3),\dots,\alpha ^{(1)}x^{(0)}(n)]^T = [x^{(0)}(2)-x^{(0)}(1),[x^{(0)}(3)-x^{(0)}(2),\dots, x^{(0)}(n)-x^{(0)}(n-1)]^T ,\mathbf{B}=\left[−x(0)(2)−z(1)(2)1⋮⋮⋮−x(0)(n)−z(1)(n)1\right] u=[a1,a2,b]T,Y=[α(1)x(0)(2),α(1)x(0)(3),…,α(1)x(0)(n)]T=[x(0)(2)−x(0)(1),[x(0)(3)−x(0)(2),…,x(0)(n)−x(0)(n−1)]T,B=⎣ ⎡−x(0)(2)⋮−x(0)(n)−z(1)(2)⋮−z(1)(n)1⋮1⎦ ⎤
于是最小二乘估计为
u ^ = ( B T B ) ( − 1 ) B T Y \hat u=(\mathbf{B}^T\mathbf{B})^{(-1)}\mathbf{B}^T\mathbf{Y} u^=(BTB)(−1)BTYDGM(2,1)
与GM(2,1)模型相比,没有使用均值序列。
即基础模型为:
α ( 1 ) x ( 0 ) ( k ) + a x ( 0 ) ( k ) = b \alpha^{(1)}x^{(0)}(k)+ax^{(0)}(k) = b α(1)x(0)(k)+ax(0)(k)=b
白化方程为:
d 2 x ( 1 ) d t 2 + a d x ( 1 ) d t = b \frac{d^2x^{(1)}}{dt^2}+a\frac{dx^{(1)}}{dt}=b dt2d2x(1)+adtdx(1)=b
令 u = [ a , b ] T , Y = [ α ( 1 ) x ( 0 ) ( 2 ) , α ( 1 ) x ( 0 ) ( 3 ) , … , α ( 1 ) x ( 0 ) ( n ) ] T = [ x ( 0 ) ( 2 ) − x ( 0 ) ( 1 ) , [ x ( 0 ) ( 3 ) − x ( 0 ) ( 2 ) , … , x ( 0 ) ( n ) − x ( 0 ) ( n − 1 ) ] T , B = [ − x ( 0 ) ( 2 ) 1 ⋮ ⋮ − x ( 0 ) ( n ) 1 ] \mathbf{u}=[a,b]^T, \mathbf{Y}=[\alpha ^{(1)}x^{(0)}(2), \alpha ^{(1)}x^{(0)}(3),\dots,\alpha ^{(1)}x^{(0)}(n)]^T = [x^{(0)}(2)-x^{(0)}(1),[x^{(0)}(3)-x^{(0)}(2),\dots, x^{(0)}(n)-x^{(0)}(n-1)]^T ,\mathbf{B}=\left[−x(0)(2)1⋮⋮−x(0)(n)1\right] u=[a,b]T,Y=[α(1)x(0)(2),α(1)x(0)(3),…,α(1)x(0)(n)]T=[x(0)(2)−x(0)(1),[x(0)(3)−x(0)(2),…,x(0)(n)−x(0)(n−1)]T,B=⎣ ⎡−x(0)(2)⋮−x(0)(n)1⋮1⎦ ⎤
于是最小二乘估计为
u ^ = ( B T B ) ( − 1 ) B T Y \hat u=(\mathbf{B}^T\mathbf{B})^{(-1)}\mathbf{B}^T\mathbf{Y} u^=(BTB)(−1)BTY

Verhulst模型
Verhulst模型主要用来描述具有饱和状态的过程,即S形过程,常用于人口预测、生物生长、繁殖预测及产品经济寿命预测等。
Verhulst基本模型为:
x ( 0 ) + a z ( 1 ) = b ( z ( 1 ) ) 2 x^{(0)}+az^{(1)}=b(z^{(1)})^2 x(0)+az(1)=b(z(1))2
对应的白化方程为:
d x ( 1 ) d t + a x ( 1 ) = b ( x ( 1 ) ) 2 , t 为时间 \frac{dx^{(1)}}{dt}+ax^{(1)}=b(x^{(1)})^2,t为时间 dtdx(1)+ax(1)=b(x(1))2,t为时间
令 u = [ a , b ] T , Y = [ x ( 0 ) ( 2 ) , … , x ( 0 ) ( n ) ] T , B = [ − z ( 1 ) ( 2 ) ( z ( 1 ) ( 2 ) ) 2 ⋮ ⋮ − z ( 1 ) ( n ) ( z ( 1 ) ( n ) ) 2 ] \mathbf{u}=[a,b]^T, \mathbf{Y}=[x^{(0)}(2),\dots,x^{(0)}(n)]^T ,\mathbf{B}=\left[−z(1)(2)(z(1)(2))2⋮⋮−z(1)(n)(z(1)(n))2\right] u=[a,b]T,Y=[x(0)(2),…,x(0)(n)]T,B=⎣ ⎡−z(1)(2)⋮−z(1)(n)(z(1)(2))2⋮(z(1)(n))2⎦ ⎤
于是最小二乘估计为
u ^ = [ a ^ , b ^ ] T = ( B T B ) ( − 1 ) B T Y \hat u=[\hat a,\hat b]^T=(\mathbf{B}^T\mathbf{B})^{(-1)}\mathbf{B}^T\mathbf{Y} u^=[a^,b^]T=(BTB)(−1)BTY

写在最后:
不难看出后面的内容灌水了,但学起来真的太累,这篇内容主要摘自《数学建模算法与应用(第二版)》司守奎 孙兆亮主编,但书中有一些简略(换句话说:自己的能力还有待提高),像我这样的小白还得多百度看看大佬们的讨论,才能更好理解思路。总的来说,对GM(1,1)了解个七七八八了,对其它就是略知一二,先码在这儿吧,等实践用了之后再回来补充。 -
相关阅读:
人工智能-机器学习-深度学习-概述
Python语言学习:Python语言学习之列表/元祖/字典/集合的简介、案例应用之详细攻略
vue路由之路由的两种模式
python基于百度sdk语音转文字
每章一篇博客带你拿下吉林大学JAVAEE期末(八)
边沿D触发器
C++ 获取网卡名称和IP地址
ArcGIS加载的各类地图怎么去除服务署名水印
创建自定义 Spring Cloud Gateway 过滤器 - spring.io
融合注意力机制和BSRU的工业互联网安全态势预测方法
- 原文地址:https://blog.csdn.net/Z__XY_/article/details/126689413