• 快速排序(QuickSort)

    下面是以升序排序为例进行讲解的。

    因为要分别讲解三种方法，为了避免代码冗余，代码部分是将每种方法的实现代码单独抽了出来。

    文章目录

    核心思想

    快速排序算是交换排序的一种，是通过多次比较和交换来实现排序。

    其核心思想是指定一个分界值 key ，

    用 key 来分割数组，

    通过多次比较和交换使得 key 左边的数据都比它小，

    右边的数据都比它大，

    那么整体就是有序的。

    对 key 的左半部分和右半部分分别重复上述过程，

    最终整个数组就是有序的了。

    下面将用一步步图解的方式分别讲解三种实现方法去理解上述过程。

    单趟排序实现方法

    左右指针法

    首先要指定一个 key ，指定最左边或最右边的元素最为方便，这里是以数组第一个元素作为 key 的，不过为了统一一点，这里用了下标：

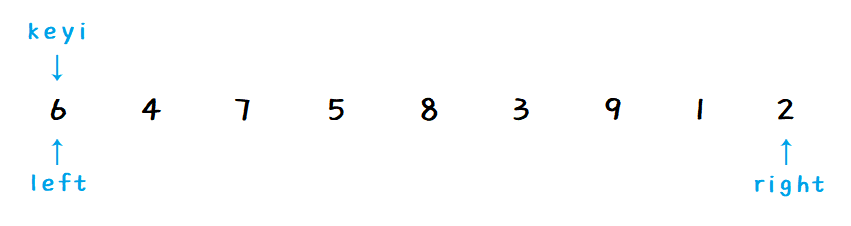
    image-20220904131214968

    1. 如果是以第一个元素作为 key ，那么 right 要先走，寻找比 key 小的数，这里刚好符合。

      （如果是以最后一个元素作为 key ，那么 left 要先走，寻找比 key 大的数）

    2. 然后 left 接着走，寻找比 key 大的数：

      image-20220904131943324

    3. right 和 left 进行交换：

      image-20220904131902665

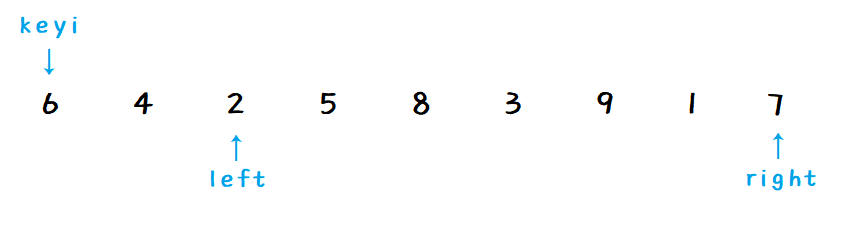
    4. 继续迭代，right 向左找比 key 小的数：

      image-20220904132139562

    5. left 继续向右找比 key 大的数：

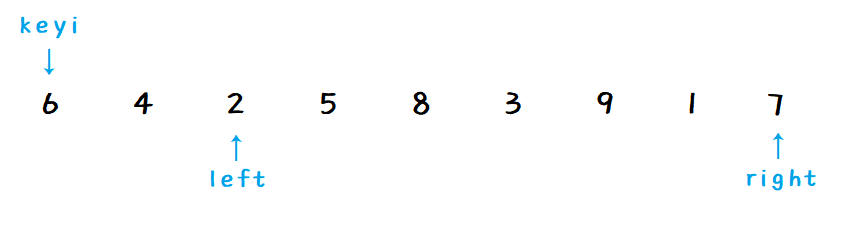
      image-20220904132316910

    6. right 和 left 进行交换：

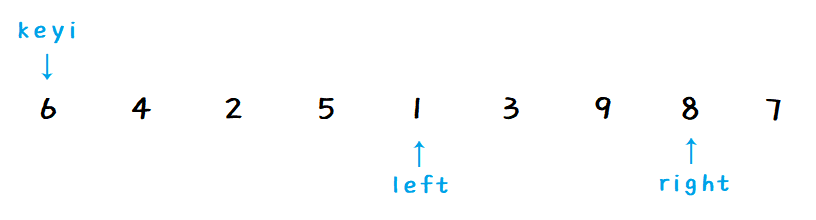
      image-20220904132442804

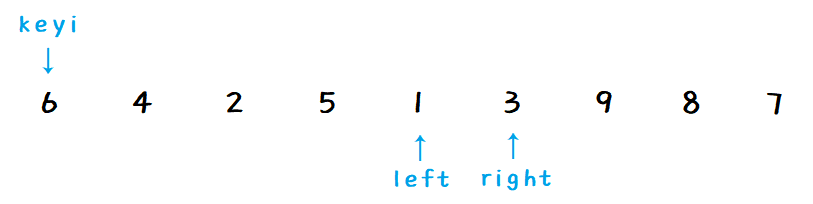
    7. right 继续向左找比 key 小的数：

      image-20220904132557326

    8. left 继续向右找比 key 大的数，right 和 left 相遇时就停止：

      image-20220904132735012

    9. 交换 key 和 left ：

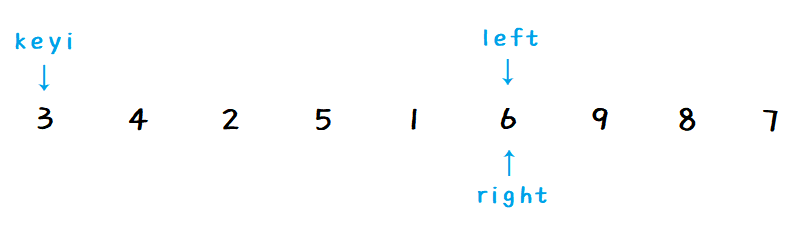
      image-20220904132831668

    至此，就完成了一次单趟排序，指定的 key = 6 左侧元素都比它小，右侧元素都比它大。

    对它左半部分和右半部分再分别走上面的流程，递归下去，最后整个数组就有序了。

    如果写成函数的形式 ，应将 left 下标返回，因为这是数组的分界点。

    这种方法的代码实现如下：

    int SortMethod1(int* a, int left, int right) {
	int keyi = left;
	while (left < right) {
		//先右边找小
		while (left < right && a[right] >= a[keyi])
			--right;
		//然后左边找大
		while (left < right && a[left] <= a[keyi])
			++left;
		Swap(&a[left], &a[right]);
	}
	Swap(&a[keyi], &a[left]);
	return left;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    挖坑法

    还是先指定一个 key ，这里还是以数组第一个元素为 key。

    跟前后指针一样，这里也有左右两个指针，不过需要先保存一下 key ，最后会留一个坑位放它：

    image-20220904135742338

    1. 先右边找比 key 小的数，然后把 right 赋给 left ：

      image-20220904140145011

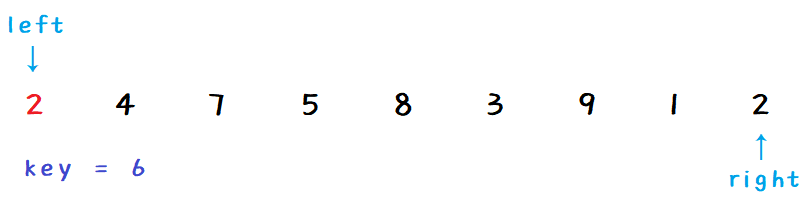
    2. 再左边找比 key 大的数，然后把 left 赋给 right ：

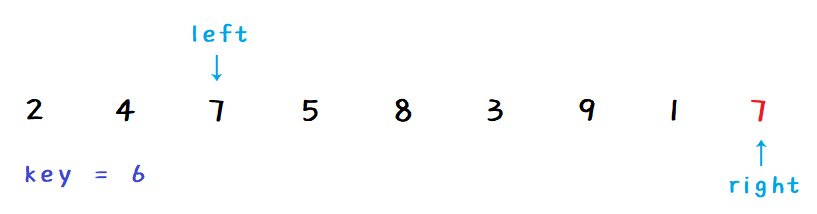
      image-20220904153424821

    3. right 继续找小，然后把 right 赋给 left ：

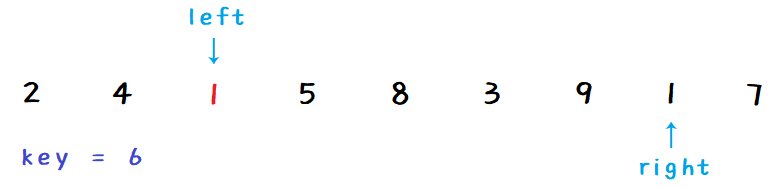
      image-20220904153644451

    4. left 继续找大，然后把 left 赋给 right：

      image-20220904153850906

    5. right 继续找小，然后把 right 赋给 left ：

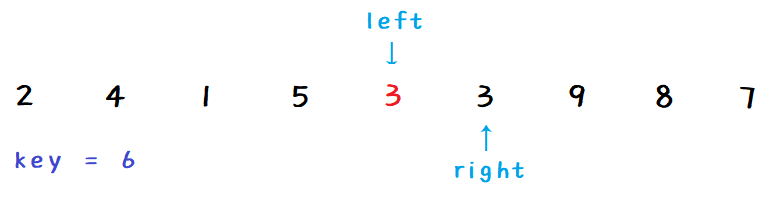
      image-20220904154021419

    6. left 继续找大，与 right 相遇时就停下，然后将 key 赋给 left：

      image-20220904154342466

    至此，就完成了一次单趟排序，key = 6 的左侧元素都比它小，右侧元素都比它大。

    再分别对它的左半部分和右半部分重复上述过程，最后数组就有序了。

    如果写成函数的形式 ，应将 left 下标返回，因为这是数组的分界点。

    这种方法的代码实现如下：

    int SortMethod2(int* a, int left, int right) {
	int key = a[left];
	while (left < right) {
		while (left < right && a[right] >= key)
			--right;
		a[left] = a[right];
		while (left < right && a[left] <= key)
			++left;
		a[right] = a[left];
	}
	a[left] = key;
	return left;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    前后指针法

    还是以数组第一个元素为 key ，设两个指针 cur 和 prev ：

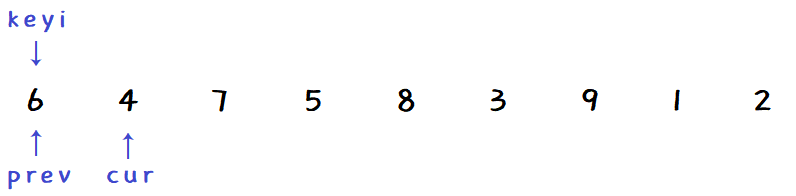
    image-20220904161646808

    这个方法的核心是 cur 找小，prev 找大，然后交换，重复上述过程至完成一边遍历。

    如果 cur 指向的比 key 小，像上面那样，如果交换的话，key 就会丢失，所以此时 prev 和 cur 都要向前一步。

    如果 cur 指向的比 key 小，prev 经过交换后也会指向比 key 小的，此时二者如果相邻，交换也没意义，也应都向前走一步；如果二者不相邻，prev + 1 就是比 key 大的元素，先对 prev + 1 然后交换即可。

    总结一下就是，prev 和 cur 相邻时不交换，要交换时 prev 要先 +1。

    1. cur 指向的比 key 小，但二者相邻，不交换，都向前走一步：

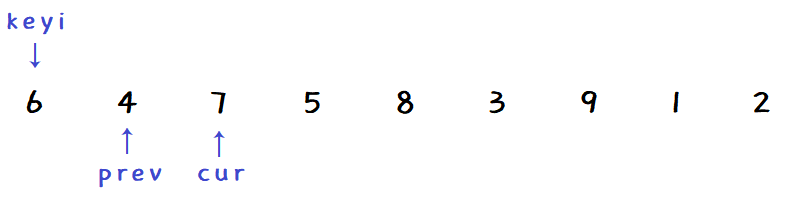
      image-20220904165847170

    2. cur 向前找小：

      image-20220904170016368

    3. prev 与 cur 不相邻，+1 后交换：

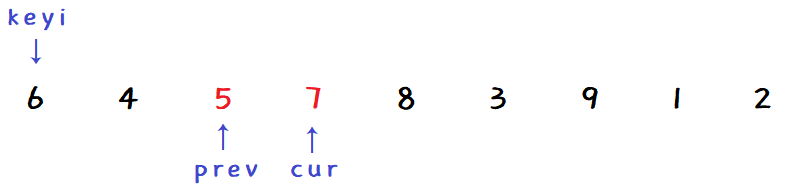
      image-20220904170327152

    4. cur 继续向前找小：

      image-20220904170618633

    5. prev 与 cur 不相邻，+1 后交换：

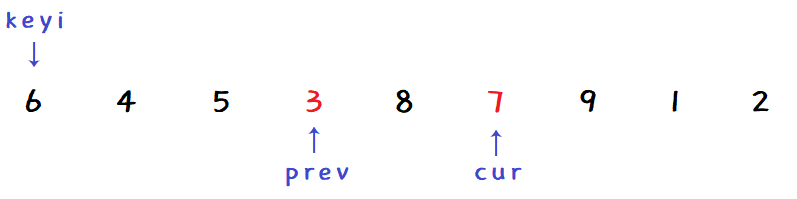
      image-20220904170821749

    6. cur 继续向前找小：

      image-20220904171047653

    7. prev 与 cur 不相邻，+1 后交换：

      image-20220904171215747

    8. cur 继续向前找小：

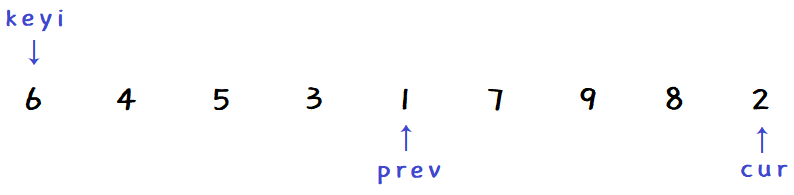
      image-20220904171400617

    9. prev 与 cur 不相邻，+1 后交换：

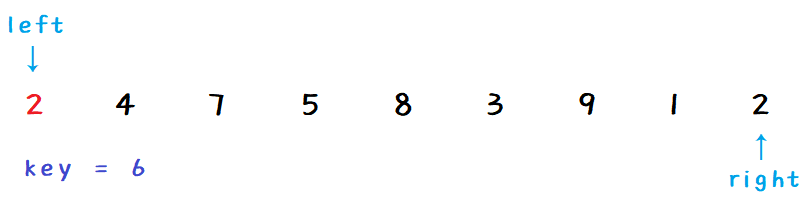
      image-20220904171531607

    10. 当 cur 走到末尾时，交换 keyi 和 prev：

      image-20220904171720490

    至此，就完成了一次单趟排序，key = 6 的左侧元素都比它小，右侧元素都比它大。

    再分别对它的左半部分和右半部分重复上述过程，最后数组就有序了。

    如果写成函数的形式 ，应将 prev 下标返回，因为这是数组的分界点。

    这种方法的代码实现如下：

    int PartMethod3(int* a, int left, int right) {
	int keyi = left;
	int prev = left;
	int cur = prev + 1;
	while (cur <= right) {
		if (a[cur] < a[keyi] && ++prev != cur)
			Swap(&a[cur], &a[prev]);
		++cur;
	}
	Swap(&a[prev], &a[keyi]);
	return prev;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12

    因为判断交换时 prev 和 cur 无论相不相邻，prev都要 +1 ，所以代码中将判断相邻和 prev + 1 简写了一下。

    时间复杂度分析

    因为快速排序并没有占用额外的空间，所以空间复杂度是 O(1)，无需对其进行讨论。

    当每次选的 key 都是区间的中位数时，

    当每次选的 key 都是数组的中位数时，

    每次单趟排序都能将数组平均划分为两块，

    这样只需进行 log2n 次单趟排序数组就会有序。

    由于每次单趟排序都是一次完整的遍历，

    所以单趟排序的时间复杂度就是 O(N)，

    总体的时间复杂度就是 O(NlogN) 。

    但是，

    如果每次选的 key 都是该区间的最大或最小值，

    那么每次单趟排序就不起分割作用，

    总共需要进行 n 次单趟排序，

    此时就退化成了选择排序，

    时间复杂度退化为 O(N2) 。

    优化

    三数取中优化

    上面的最坏情况发生在选的 key 是最值的情况下，那么最直接的优化方法就是让 key 不是最值。

    这一点可以通过三数取中完成。

    选三个数，这里选择左右端点和中间位置的三个数。

    通过比较，返回三个数的中位数的下标，

    然后将 key 和上面得到的中位数进行交换，

    这样就可以保证 key 不会是最值了。

    代码如下：

    int GetMid(int* a, int left, int right) {
	int mid = left + (right - left) / 2;
	if (a[left] < a[mid] && a[mid] < a[right])
		return mid;
	else if (a[right] < a[mid] && a[mid] < a[left])
		return mid;
	else if (a[mid] < a[left] && a[left] < a[right])
		return left;
	else if (a[right] < a[left] && a[left] < a[mid])
		return left;
	else if (a[mid] < a[right] && a[right] < a[left])
		return right;
	else
		return right;
}

//对挖坑法进行优化
int PartMethod2(int* a, int left, int right) {
	int midindex = GetMid(a, left, right);
	Swap(&a[left], &a[midindex]);

	int key = a[left];
	while (left < right) {
		while (left < right && a[right] >= key)
			--right;
		a[left] = a[right];
		while (left < right && a[left] <= key)
			++left;
		a[right] = a[left];
	}
	a[left] = key;
	return left;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    小区间优化

    了解插入排序的朋友们应该知道，当数组越接近有序时插入排序的效率越高。

    当快速排序递归到一定深度时，区间已经缩地比较小了，递归的深度也已经很深了，此时可以考虑对小区间使用插入排序进行优化。

    但这种优化方法相比三数取中效果不那么明显，所以了解即可，从实用的角度不必深究。

    递归和非递归实现快速排序

    递归版本

    递归是快速排序最正统的解法，相对也比较简单。

    以挖坑法为例，如果用上面封装的函数实现起来就是下面这样：

    void QuickSort(int* a, int begin, int end) {
	if (begin >= end)
		return;
		
    int keyi = PartMethod2(a, begin, end);
    
    QuickSort(a, begin, keyi - 1);
    QuickSort(a, keyi + 1, end);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9

    如果没有封装函数直接写的话就是这样：

    void QuickSort(int* a, int begin, int end) {
	if (begin >= end)
		return;
		
    //三数取中优化
    int midindex = GetMid(a, begin, end);
	Swap(&a[begin], &a[midindex]);
    
    int left = begin, right = end;
	int key = a[left];
	while (left < right) {
		while (left < right && a[right] >= key)
			--right;
		a[left] = a[right];
		while (left < right && a[left] <= key)
			++left;
		a[right] = a[left];
	}
	a[left] = key;
    
    QuickSort(a, begin, left - 1);
    QuickSort(a, left + 1, end);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    非递归版本

    快速排序的非递归实现要借助栈来模拟递归。

    首先有关栈的接口功能如下：

    void StackInit(Stack* ps); //初始化
void StackPush(Stack* ps, int val); //入栈
void StackPop(Stack* ps); //出栈
void StackTop(Stack* ps); //取栈顶数据
void StackEmpty(Stack* ps); //判空
void StackDestroy(Stack* ps); //销毁栈

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6

    首先将区间的端点下标入栈，然后开始迭代。

    首先取到栈顶的两个数据作为第一趟排序的区间，

    第一趟排完之后会将区间分割，

    如果两个小区间还需要继续排序，

    则将两个小区间的端点继续入栈，

    如此往复…

    当栈为空时，说明所有区间都已排好，

    此时排序就完成了。

    代码如下：

    void QuickSortNonR(int* a, int begin, int end) {
	Stack st;
	StackInit(&st);
	StackPush(&st, begin);
	StackPush(&st, end);
	while (!StackEmpty(&st)) {
		int right = StackTop(&st);
		StackPop(&st);

		int left = StackTop(&st);
		StackPop(&st);

		int keyi = PartMethod2(a, left, right);

		if (keyi - 1 > left) {
			StackPush(&st, left);
			StackPush(&st, keyi - 1);
		}

		if (keyi + 1 < right) {
			StackPush(&st, keyi + 1);
			StackPush(&st, right);
		}
	}
	StackDestroy(&st);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26

    如果不封装成函数直接写的话代码如下：

    void QuickSortNonR(int* a, int begin, int end) {
	Stack st;
	StackInit(&st);
	StackPush(&st, begin);
	StackPush(&st, end);
	while (!StackEmpty(&st)) {
		int right = StackTop(&st);
		StackPop(&st);

		int left = StackTop(&st);
		StackPop(&st);
        
        int tmpR = right, tmpL = left;

		//三数取中优化
        int midindex = GetMid(a, left, right);
        Swap(&a[left], &a[midindex]);

        int key = a[left];
        while (left < right) {
            while (left < right && a[right] >= key)
                --right;
            a[left] = a[right];
            while (left < right && a[left] <= key)
                ++left;
            a[right] = a[left];
        }
        a[left] = key;

		if (left - 1 > tmpL) {
			StackPush(&st, tmpL);
			StackPush(&st, left - 1);
		}

		if (left + 1 < tmpR) {
			StackPush(&st, left + 1);
			StackPush(&st, tmpR);
		}
	}
	StackDestroy(&st);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41

    稳定性分析

    排序算法的稳定性并不是指这个算法的复杂度会因数据的不同而发生改变。

    排序算法的稳定性指的是假设数组中有两个相等的数据，这两个数据在排序前后的相对位置不发生改变，那么这个排序算法就是稳定的，否则是不稳定的。

    举个例子，假设有一群同学考试，答完试卷即可交卷。A 同学和 B 同学都考了满分，但 A 同学交卷比 B 早，所以综合起来 A 同学的排名更高。此时同学们的顺序是按交卷顺序排的。对同学们按分数高低进行排序，A 本来在 B 前面，如果用不稳定的排序算法，排完之后 A 同学可能就在 B 同学的后面了，这并不是正确的结果。

    所以排序算法的稳定性还是有一定的意义。

    那快速排序是稳定的吗？

    以下面一组数据为例：

    5, 3, 3, 4, 3, 8, 9, 10, 11

    以左右指针法为例，key = 5，

    right 找小，left 找大，最终会在 3 相遇：

    image-20220904192413471

    下一步就要交换 5 和 3 ，仅仅一趟三个 3 的相对位置就发生了变化，

    显然，快速排序是不稳定的。

    一个排序算法的不稳定性是比较好证明的，只需要找出一组不符合的数据即可。

    而一个稳定的排序算法是不好证明的。

    常见排序算法中稳定的有：冒泡排序、插入排序、归并排序

    不稳定的有：堆排序、快速排序、希尔排序、选择排序

    但稳定的排序算法并不是绝对稳定。

    以冒泡排序为例，当两个数据相等时如果也让它们交换，那相对顺序就发生了变化，冒泡排序就会变得不稳定。

  • 相关阅读:
    pta(浙大第四版)五道经典练习题③
    链接装载与库：第四章——静态链接
    【GNN】图技术在美团外卖下的场景化应用及探索（更新ing）
    CICD：使用docker+ jenkins + gitlab搭建cicd服务
    Unity基础课程之物理引擎7-物理运动应该在FixedUpdate执行
    FoFa 查询工具（fofax）
    基于 Debian 12 的 Devuan GNU+Linux 5 为软件自由爱好者而生
    vue中的事件处理
    网络安全-隔离技术
    Spring Framework 远程命令执行漏洞CVE-2022-22965
  • 原文地址：https://blog.csdn.net/Ye_Ming_OUC/article/details/126693296