【推荐系统】推荐系统-基础算法 基于社交网络的算法

目录

基于用户的推荐在社交网络中的应用

1、对于用户u和用户v，可以使用共同好友比例计算他们的相似度：

​编辑

2、使用共同被关注的用户数量计算用户之间相似度

3、第三种有向的相似度：这个相似度的含义是用户u关注的用户中，有多大比例也关注了用户v：

node2vec在社交网络推荐中的应用

1.random walk

2.Word2Vec

Skip—Gram

在一个句子中选取上下文词

将训练样本输入模型：

神经网络结构的隐藏层(对应词向量)：

CBOW模型

3、node2vec的训练

---

社交网络形成两类社交网络结构，一类是好友一般都是自己在现实中认识的，这种好友关系需要双方确认，如qq空间，facebook,称之为社交图谱。另一种好友只是出于对对方的言论感兴趣而建立好友关系，是单向的，如微博，twitter。这种社交网络也被成为兴趣图谱。但任何一个社会化网站都不是单纯的社交图谱或兴趣图谱，在熟人网络如qq空间也会和部分好友有共同兴趣而在微博这种兴趣图谱社交网站中也可能会有现实生活中的亲朋好友.

基于用户的推荐在社交网络中的应用

用图G（V，E，W）定义一个社交网络，其中V是顶点集合，每个顶点代表一个用户，E是边集合，如果用户Va和Vb有社交网络关系，那么就有一条边e(Va,Vb)连接这两个用户，W(Va,Vb）用来定义过的权重，前面提到基于社交图谱或兴趣图道的两种社交网络，基于社交用请的朋友关系是需要双向确认的，因而可以用无向边连接有社交网络关系的用户；基于兴趣图谱的化关系是单向的，可以用有向边代表这种社交网络上的用户关系。

一般在图中，对于用户顶点u，定义out（u）为顶点u指向的顶点集合（也就是用户关注的用户集合），定义in(u)为指向顶点u的顶点集合（也就是关注用户u的用户集合）。显然在无向社交网络中out(u)=in(u)。一般来说，有如下3种不同的社交网络数据。

• 双向确认的社交网络数据：在以Facebook和人人网为代表的社交网络中，用户A和B之间形成好友关系需要通过双方的确认。因此，这种社交网络一般可以通过无向图表示。
• 单向关注的社交网络数据：在以Twitter 和新浪微博为代表的社交网络中，用户A可以关注用户B而不需要得到用户B的允许，因此这种社交网络中的用户关系是单向的，可以通过有向图表示。
• 基于社区的社交网络数据：还有一种社交网络数据，用户之间并没有明确的关系，但
• 这种数据包含了用户属于不同社区的数据，用户可能共同关注了某个话题，他们兴趣相似，但是却没有真正建立好友关系。

有了用户之间的网络关系，我们需要进一步把用户与物品之间的关系融合进来。

基于用户的协同推荐算法，主要思路是使用用户与物品之间的关系计算用户相似度。那么有了用户关系数据之后，我们同样可以使用用户好友或关注的数据计算用户之间的相似度，主要有以下几种方法：

1、对于用户u和用户v，可以使用共同好友比例计算他们的相似度：

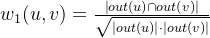
out(u)指在社交网络图中用户u指向的其他好友的集合。分母定义用户u和用户u共同指向好友的数量。在实际生产环境中，用户的量级往往比较大，且数据库中存储的一般是好友关系对这样的二元数据，因此建议使用Spark 中 Graphx模块去计算共同好友数量，相较于Python可以提升3倍以上的计算效率。

2、使用共同被关注的用户数量计算用户之间相似度

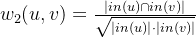
in（u）是指用户u被其他用户指向的集合。在无向社交网络图中，out(u)和in(u)是 相同的集合。但在微博这种有向社交网络中，这两个集合的含义就不同了。这种方法适用于计算大V之间的相似度，因为大V往往被关注的人数比较多；而第一种方法适用于计算普通用户的兴趣相似度，因为普通用户往往关注行为比较丰富。

3、第三种有向的相似度：这个相似度的含义是用户u关注的用户中，有多大比例也关注了用户v：

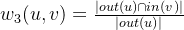
这个相似度有一个缺点，就是在该相似度的定义下所有人都和大V有很大的相似度，因为分母没有考虑in(u)的大小，所以将in(u)加入分母,来降低大V和其他用户的相似度。

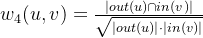
有了基于社交网络的用户相似度数据，结合基于用户协同中的相似度共同计算出新的相似度分数：

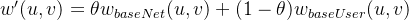
再针对用户u挑选k个最相似的用户，把他们购买过得物品中，u未购买的物品推荐给用户u即可.如果有评分数据，可以针对这些物品进一步打分，打分的原理与基于用户的协同过滤原理类似

node2vec在社交网络推荐中的应用

 对于大规模社交关系，离线计算用户相似度并存储下来以供线上推荐系统使用不合理，用一个坐标表示来描述用户在社交网络中的位置？这样只需提前计算好用户坐标，线上计算用户之间的相似度时，只要计算坐标的距离或者余弦相似度即可。可以通过 network embedding 的方法来计算用户的坐标。network embedding 就是一种图特征 的表示学习方法，它从输入的网络图中，学习到节点的表达。

node2vec的整体思路分为两个步骤：

•  random walk（随机游走），即通过一定规则随机抽取一些点的序列。
•  将点的序列输入至Word2Vec模型从而得到每个点的embedding向量。

1.random walk

random walk的基本流程，给定一张图G和一个起始节点S，标记起始节点位置为当前位置，随机选择当前位置节点的一个邻居并将当前位置移动至被选择的邻居位置，重复以上步骤n次，最终会得到从初始节点到结束节点的一条长度为n的“点序列”，此条“点序列”即称为在图G上的一次 random walk。

假设我们的起始节点为A，随机游走步数为4。首先从A开始，有B、E两个节点可游走到，我们随机选择B；再从B开始，有A、E、F三个备选下一节点，随机选择节点为F；再从F开始，于B、C、D、E四个节点，我们随机取C；再从C开始，游走到H，这样我们就获取了一条 random walk 路径：A→B→B→F→C→H

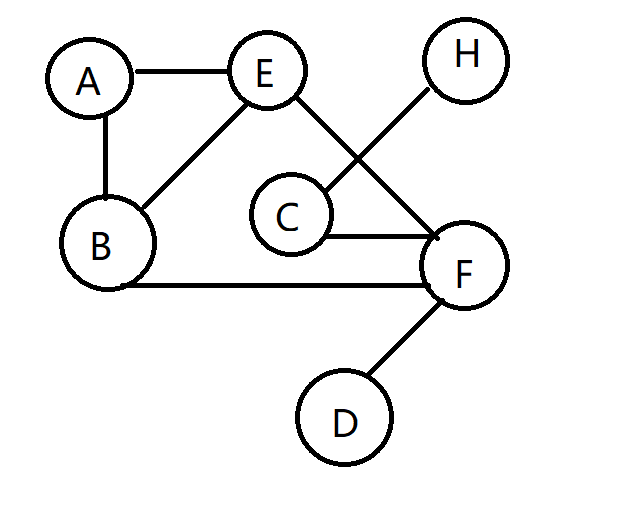
random walk 算法主要分为两步：（1）选择起始节点；（2）选择下一跳节点。其中起始节点的选择存在两种常见做法，其一，按照一定规则随机从图中抽取一定数量的节点；其二，以图中所有节点作为起始节点。一般来说我们选择第2种方法，以使所有节点都会被选取到。

如何选择下一跳节点：最简单的方法是按照边的权重随机选择；但是在实际应用中，我们希望能控制广度优先还是深度优先，从而影响random walk 能够游走到的范围。一般来说，深度优先的方法，发现能力更强；广度优先的方法，社区内的节点更容易出现在一个路径里。斯坦福大学计算机教授 Jure Leskovec给出了一种可以控制广度优先或者深度优先的方法。

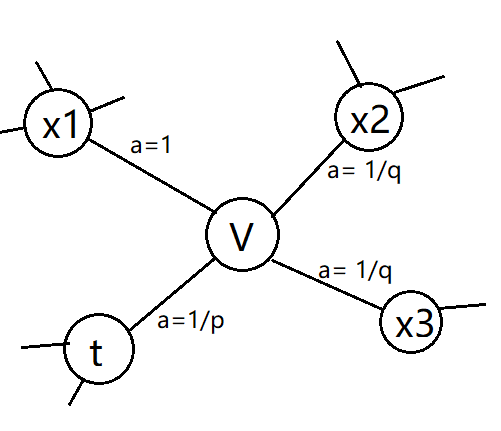
以图4.23为例，我们假设第一步是从t随机游走到v，这时候我们要确定下一步的邻接节点。在本例的随机游走中，定义p和q两个参数变量来调节游走，首先计算其邻居节点与上一节点t的距离d，根据公式得到。

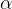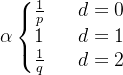
下一节点选择为t，即往回走的时候，d=0;当下一节点为x1时，u、t和x1构成 三角形，d=1；当下一节点为或者 时， d=2这时根据a的值确定下一节点的选 择概率。如果大于max (q,1)，则产生的序列与深度优先搜索类似，刚刚被访问过的节 点不太可能被重复访问；反之，如果小于m in(q,1)，则产生的序列与宽度优先搜索类 似，倾向于周边节点。

至此，我们就可以通过random walk生成点的序列样本。一般来说，我们会从每个 点开始游走5～10次，步长则根据点的数量N游走✓N步。

2.Word2Vec

上一步中获得了点的序列样本，那么下一步需要解决如何根据点序列生成每个点的特征向量，

Word2Vec已成为现在主流的特征构造方法。Word2Vec是从大量文本语料中以无监督的方式学习语义知识的一种模型，它被大量地运用在自然语言处理（NLP）中。Word2Vec的核心目标是通过一个嵌入空间将每 个词映射到一个空间向量上，并且使得语义上相似的单词在该空间内距离很近。举个例子，“国王”这个单词和“王子”属于语义上很相近的词，而“国王”和“公主”则不是那 么相近，“国王”和“小丑”则就差得更远了。通过Word2Vec的学习，可以得到每个词的数值向量，例如（0.23，0.45，0.01···．），我们希望“国王”和“王子”的数值向量比较接近， 而“国王”和“小丑”的数值向量相差较远。数值向量化的操作也能帮助我们得到一些有趣的结论，例如“国王”—“王子”＝“女王”—“公主”。

Word2Vec模型中，主要有 Skip-Gram和CBOW两种模型

• Skip—Gram

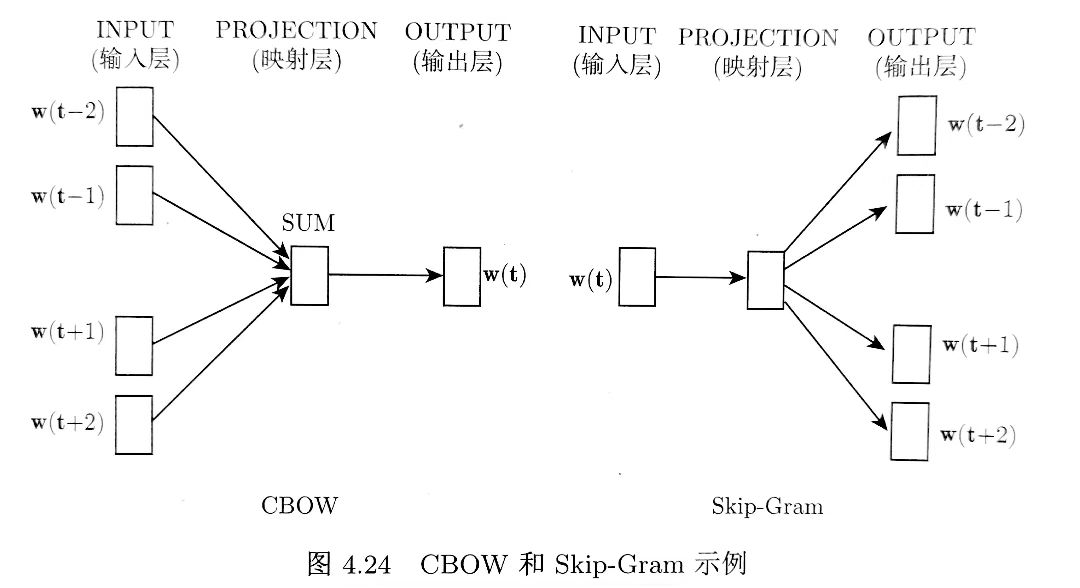
模型实际上分为两个部分，第一部分为建立模型，第二部分是通过模型获取嵌入词向量。整个建模过程实际上与中自编码器的思想很相似，即先基于训练数据构建一个神经网络，当这个模型训练好以后，我们并不会用这个训练好的模型处理新的任务，我们真正需要的是这个模型通过训练数据所学得的参数，例如隐层的权重矩阵，正是我们希望得到的词向量。训练模型的目的是为了获得模型基于训练数据学得的隐藏权重。

在一个句子中选取上下文词

再定义参数skipwindow，选取上下文词两侧获得词的数目，如I am a beautiful girl and I love study这个句子，选取girl作为上下文词，skipwindow = 2，则取到的训练样本为：girl-> (a ，beautiful)， (and， I )，将训练样本输入到Skip-Gram模型中。

将训练样本输入模型：

神经网络只能接受数值输入，不可能把一个单词字符串作为输入，最常用的办法就是基于训练文档来构建我们自己的词汇表（vocabulary），再对单词进行 one—hot编码。假设从我们的训练文档中抽取出10000个唯一不重复的单词组成词汇表。我们对这10000个单词进行one—hot编码，得到的每个单词都是一个10000维的向量，向量每个维度的值只有0或者1。假如单词“world'”在词汇表中的出现位置为第3个，那么world的向量就是一个第三维度取值为1，其他维都为0的10000维的向量(world=0,0,1,0,.....0）。观察Skip—Gram 模型的输入如果为一个10000维的向量，那么输出也是一个10000维（词汇表的大小）的向量，它包含了10000个概率，每一个概率代表着当前词是输入样本中output word 的概率大小。

基于成对的单词来对神经网络进行训练，训练样本是（input word，output word）这样的单词对，例如样本（world）-＞（the，whole，is，about）。且 input word 和 output word 都是 one-hot 编 码的向量。最终模型的输出是一个概率分布。

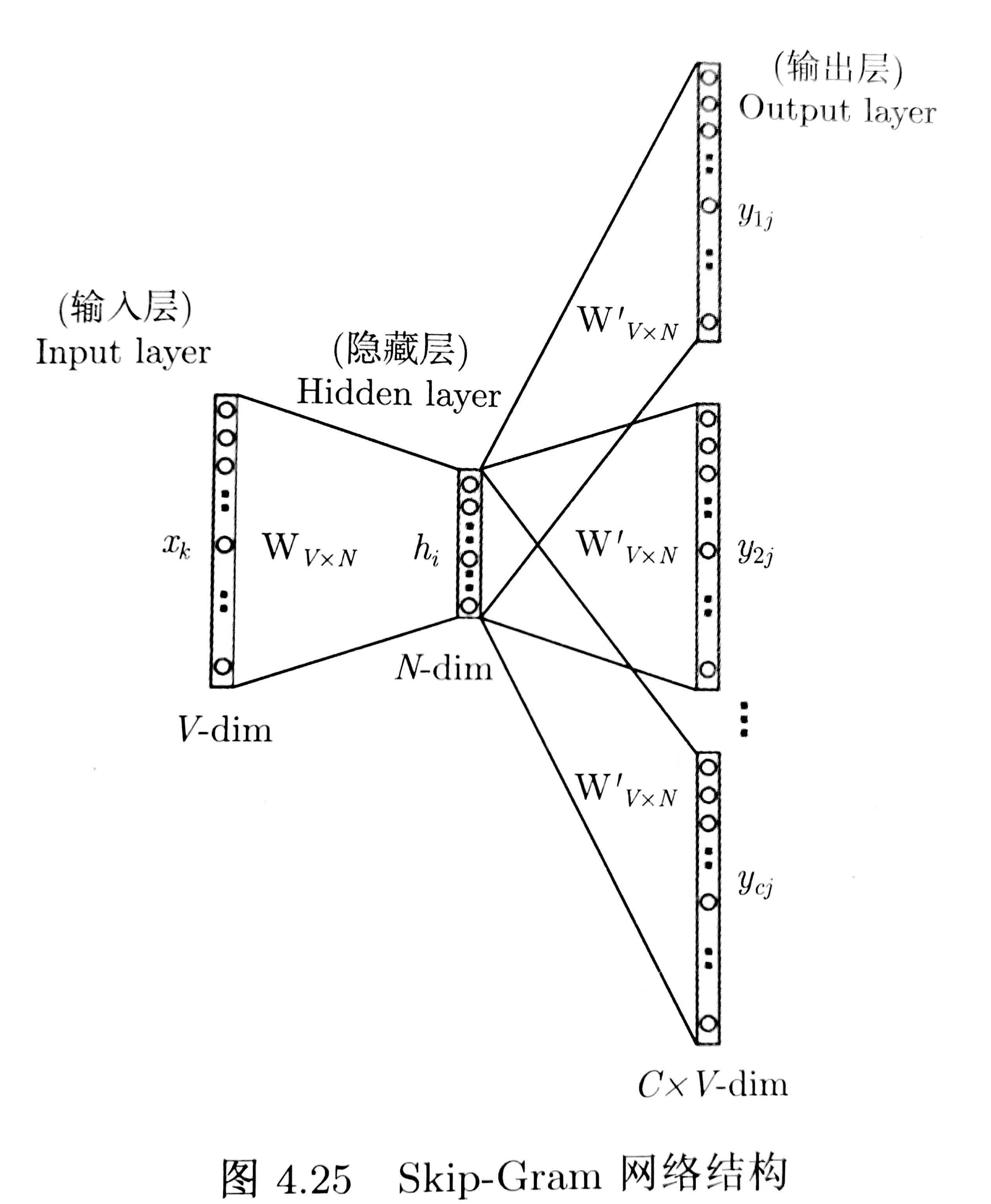
神经网络结构的隐藏层(对应词向量)：

如果我们现在想用300个特征来表示一个单词（每个单词可以被表示为300维的向量）。那么隐藏层的权重矩阵应该为10000行，300列（隐藏层有300个节点）。这300列的向量就对应了我们输入单词的词向量。

Google 在最新发布的基于 Google News 数据集训练的模型中使用的就是300个特征的词向量。词向量的维度是一个可以调节的超参数（在Python的gensim包中封装的Word2Vec接口默认的词向量大小为100，windowsize为5）。

那么为什么“国王”和“王子”的数值向量比较接近，而“国王”和“小丑”的数值向量相差较远呢？正如上面提到的Word2Vec 模型的输出是一个概率分布，基于大量的语料数据，“国王”和“王子”前后的词出现的概率比较接近，所以训练得到的词向量也会比较接近，而“国王”和“小丑”的前后文往往不一样，所以得到的词向量也会不一样。

• CBOW模型

与Skip-Gram相对应，通过上下文来预测中心词，并且抛弃了词序信息。将上下文的两个词向量求平均值“糅”成一个向量作为输入，进而预测中心词

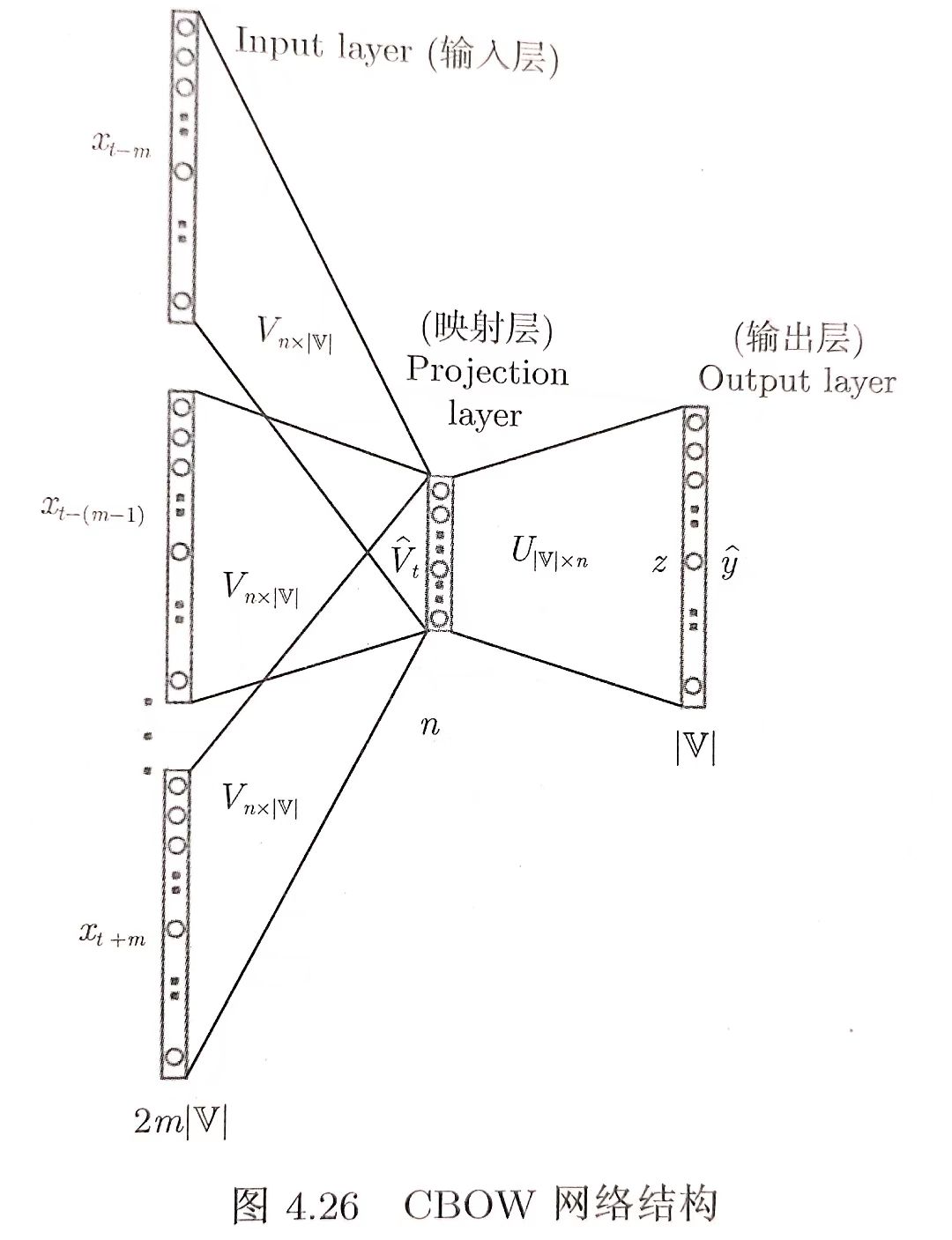
• 输入层：n个节点（one—hot向量的维度），上下文共2x skipwindow个词的词向量的平均值，即上下文2x skipwindow个词的 one-hot-representation；
• 输入层到输出层的连接边：输出词矩阵
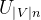
• 输出层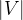：个节点。第i个节点代表中心词是词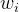的概率。

最后，word analogy是一种有趣的现象，可以作为评估词向量质量的一项任务。wordanalogy是指训练出的 word embedding 可以通过加减法操作，来对应某种关系。比如说有w（国王）-w（女王）≈ω（男人）-w（女人）。那么评测时，则是已知这个式子，给出国王、女王和男人三个词，看与w（国王）—w（女王））最接 近的是否是w(男人）。右图则表示，word analogy 现象不只存在于语义相似，也存在于语法相似。

3、node2vec的训练

思路其实就和Word2Vec基本一致。我们从上一步获得的训练样本是用户节点串，形如A→B→F→C→H→··，每一个节点其实对应了 Word2Vec中的单词，模型的输入是某个用户的one—hot编码，输出是该用户在节点串中前后的节点，例如输入是F的编码，输出是A、B、C、H的概率分布。最后得到的输出是每个节点（即用户）的Word2Vec向量。

有了数值化的向量，对于任意两个用户，我们就可以余弦或霍氏距离计算这两个用户的相似度。之后的计算过程：针对用户u挑选k个最相似的用户，把他们购买物品中u未购买过的推荐给用户u即可。为了减少计算量，我们往往会仅计算用户u和其关注用户的相似度，而不是计算用户u与所有用户的相似度。