-
分布式机器学习---数据与模型划分
数据与模型划分
当拥有大量训练数据或者大规模模型,无法由单机完成存储和计算时,就需要将数据或模型进行划分并将其分配到各个工作节点上。
数据划分
数据划分常用于训练数据很大,无法在单机上进行存储的情况。就数据划分而言,主要有两个角度:一是对训练样本进行划分,二是对每个样本的特征维度进行划分。
训练样本划分
对训练样本进行划分也有两种常用的做法:
基于随机采样:把原训练集作为采样的数据源,通过有放回的方式进行随机采样,然后按照每个工作节点的容量为其分配相应数目的训练样本。能够保证每个工作节点的局部数据与全局训练数据是独立同分布的。但是由于全局训练数据量大,全局采样的代价比较高,且会导致低频的训练样本很难被采样,没有充分利用训练样本。
基于置乱切分:将训练数据进行乱序排列,然后按照工作节点的个数将打乱后的数据顺序划分成相应的小份,随后将这些小份数据分配到各个工作节点上。需要定期地将局部数据再打乱一次,且到一定的阶段,还需要再进行全局的数据打乱和重新分配,其主要目的是使各个工作节点上的训练样本尽可能满足独立同分布的假设
有学者发现数据打乱等价或者接近于无放回的随机采样,而独立同分布的假设则暗示着有放回的随机采样。
特征维度划分
除了对训练样本进行划分,还可以考虑进行特征维度的划分。假设训练数据是以 d d d维向量的方式给出(每一维对应一个特征),我们可以将这 d 维特征顺序切分成 k k k份,然后把每份特征对应的子数据集分配到 k k k个工作节点上。
模型划分
模型划分常适用于内存不够的情况,即机器学习模型不能单独在一个计算节点上加载,因此需要将机器学习模型切分成若干子模型,然后把每个子模型放在一个工作节点上进行计算。
不同的子模型之间会有一定的依赖关系,如子模型A的输出是子模型B的输入。 因此,各个工作节点要等其输入所依赖的子模型计算完毕之后,才能开展自己的计算,而它的计算结果也将会供给依赖其输出的其他子模型进行消费。 显然,不同的子模型划分方法会影响到各个工作节点之间的依赖关系和通信强度,好的划分可以降低通信强度,提高并行计算的能力。
对模型划分时,需要考虑模型的结构特点,如划分线性模型,由于线性模型没有很强的依赖关系,因此可以直接针对不同的特征维度进行划分。而深度神经网络时高度非线性,参数之间的依赖关系很强。
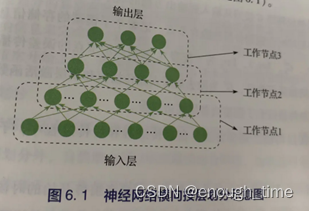
横向按层划分:(根据深度进行划分)
若神经网络很深,则一个自然且容易实现的模型并行方法就是将整个神经网络横向划分为K个部分,每个工作节点承担一层或者几层的计算任务。若计算所需要的信息本工作节点没有,则向相应的其他工作节点请求相关的信息。(横向划分的时候,通常会结合各层的节点数目,尽可能使得各个工作节点的计算量平衡)
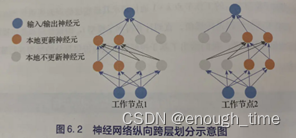
纵向跨层划分:(根据宽度进行划分)
神经网络除了深度还有宽度(通常情况下宽度会大于深度),可以将每一层的隐含节点分配给不同的工作节点。工作节点存储并更新这些纵向子网络,各个节点除了需要存储对应神经元的参数以外,还要存储每个神经元和相邻节点的神经元的关系。在前向和后传过程中,如果需要子模型以外的激活函数和误差传播值,向对应的工作节点请求相关信息进行通信。
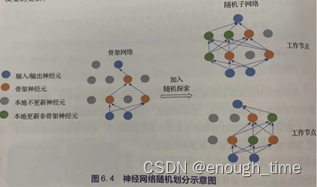
模型随机划分
由于纵向和横向划分的通信代价都比较大,因此随机划分被提出。基本思路是:神经网络具有一定的冗余性,可以找到一个规模小很多的子网络(骨架网络),其效果与原网络差不多。我们可以按照某种准则,在原网络中选出骨架网络(由服务器选取),作为公用子网络存储于每个工作节点,除骨架网络之外,每个工作节点还会随机选取一些其他节点并存储,以探索骨架网络之外的信息。股价网络周期性地依据新的网络重新选取,而用于探索的节点也会每次随机选取。有实验表明,1.模型随机并行的速度比纵向跨层划分快(尤其是复杂任务下的大规模);2.选取适当的骨架比例会使并行速度进一步提高。
-
相关阅读:
入职阿里必会199道SpringCloud面试题,你能掌握多少?
GPTS全网刷屏!定制增长速度指数增长
C语言 | Leetcode C语言题解之第329题矩阵中的最长递增路径
python:bottle + eel 模仿 mdict 查英汉词典
【Kubeedge小白安装教程】Centos7.9+K8Sv1.22.17(kubeadm)+Kubeedgev1.13.1部署教程详解(NodePort)----亲测过
买充电桩你必须要知道三件事
【Spring boot 集成 Fliter 和 Linstener】
MySQL数据类型
混合IT基础设施的安全挑战与缓解策略
每日OJ题_其它背包问题①_力扣474. 一和零(二维费用01背包)
- 原文地址:https://blog.csdn.net/sfakh/article/details/126666310