• 【推荐系统】推荐系统基础算法-基于矩阵分解的推荐方法、隐语义模型

    目录

    矩阵分解

    奇异值分解（Singular Value Decomposition，SVD）

    SVD在推荐系统中的应用

    加载用户评分矩阵，进行矩阵分解

    矩阵降维

    计算相似度

    对用户未评分过的物品进行预测 

     流程总结：

    隐语义模型

    矩阵分解

    首先我们需要知道特征值和特征向量的含义，基本定义如下：

    Ax=λx

    矩阵A是一个nxn矩阵，x是一个n维向量，则入是矩阵A的一个特征值，而ェ是矩阵A的特征值入所对应的特征向量。

    特征向量的几何含义是：特征向量x通过方阵A变换只进行缩放，而方向并不会变化。

    如果我们可以求到矩阵A的n个特征值，则可以得到对角矩阵Σ，其展开为以下形式：

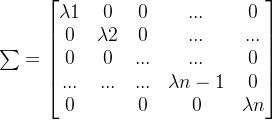
    \sum = \begin{bmatrix} \lambda 1 & 0& 0& ...& 0\\ 0& \lambda 2& 0& ...& ...\\ 0& 0& ...& ...& 0\\ ...& ...& ...& \lambda n-1& 0\\ 0& & 0& 0 & \lambda n \end{bmatrix}

    则矩阵A就可以用下式的特征分解表示：

    A=U\sum U^{-1}

    其中U是这n个特征向量所生成的nxn维矩阵，而Σ为这n个特征值为主对角线的nxn维矩阵。

    一般我们会把U的这n个特征向量标准化，即满足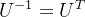U^{-1}= U^{T}，此时矩阵A的特征分解表达式可以进一步写成：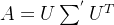

    A= U\sum^{'} U^{T}

    )那么如果A不是方阵，即行和列数目不相同时，我们还可以对矩阵进行分解吗？答案是可以。其中最常用的分解方法是奇异值分解（Singular Value Decomposition，SVD）

    奇异值分解（Singular Value Decomposition，SVD）

    SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个mxn的矩阵，那么我们定义矩阵A 的SVD为

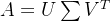
    A= U\sum V^{T}

    其中U是一个mx的矩阵，是一个mxn的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，V是一个的nxn 矩阵。

    SVD在推荐系统中的应用

    假设矩阵A的维度是10x11维，行代表用户，列代表物品，值代表用户对物品的评分，当没有评分时，分数为0,该矩阵加载到变量 myMat 中，在Python 中调用 linalg.svd 即可获得分解后的U、Σ、V三个矩阵：

    加载用户评分矩阵，进行矩阵分解

    1. from numpy import* 
    2.  
    3. #定义用户评分矩阵A
    4. def loadExData():
    5.  
    6.     return[ [0,0,1,0,0,2,0,0,0,0,5],
    7.  
    8.             [0,0,0,5,0,3,0,0,0,0,3],
    9.  
    10.             [0,0,0,0,4,1,0,1,0,4,0],
    11.  
    12.             [3,3,4,0,0,0,0,2,2,0,0],
    13.  
    14.             [5,4,2,0,0,0,0,5,5,0,0],
    15.  
    16.             [0,0,0,0,5,0,1,0,0,0,0],
    17.  
    18.             [4,1,4,0,0,0,0,4,5,0,1],
    19.  
    20.             [0,0,0,4,0,4,0,0,0,0,4],
    21.  
    22.             [0,0,0,2,0,2,5,0,0,1,2],
    23.  
    24.             [1,0,0,4,0,0,0,1,2,0,0]]
    25.  
    26. #加载用户对物品的评分矩阵
    27. myMat=mat(loadExData())
    28. #矩阵分解
    29. U,Sigma,VT=linalg.svd(myMat)
    30. print(Sigma)
    31. '''
    32. [14.2701248  11.19808631  7.13480024  5.13612006  4.68588496  3.09682859
    33.   2.72917436  2.55571761  1.05782196  0.185364  ]'''

    Sigma 为奇异值向量，可以奇异值按照从大到小排序而且奇异值的减小特别地快，在很多高维的情况下，前10％的奇异值之和就占了全部奇异值之和的80％以上的比例。本例中k的选择主要依据奇异值的能量占比，原矩阵能量值为sum(Sigma**2)=452，降低到 k=3维后能量值sum(Sigma[0:3]**2)=380，能量占比达84.4％。也就是说我们可以用最大的k个奇异值和对应u和v中的向量来描述矩阵A。

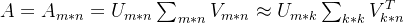
    A = A_{m*n} = U_{m*n}\sum _{m*n}V_{m*n}\approx U_{m*k}\sum _{k*k}V_{k*n}^{T}

    矩阵降维

    1. #这里取k = 4,利用矩阵分解将原来的评分矩阵降维
    2. NewData = U[:,:4] * mat(eye(4)* Sigma[:4]) * VT[:4,:]
    3. NewData

    对比两个矩阵，发现高分值都十分接近，说明可以用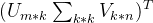(U_{m*k}\sum _{k*k}V_{k*n})^{T}这三个矩阵表征原始的矩阵A。

    将物品的评分矩阵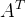A^{T}映射到低维空间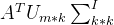A^{T}U_{m*k}\sum_{ k*k}^{I}，其中维度由nxm降到nxk,然后再计算物品item间的相似度，每个item的维度由m降到n,从而提升了计算效率。

    一般来说，m代表样本的用户数，维度会很高，而k<

    计算相似度

    1. #基于SVD的评分估计
    2. ##dataMat是输入矩阵
    3. #simMeas是相似度计算函数
    4. #user和item是待打分的用户和item对
    5. #userData是输入矩阵dataMat的子集
    6. #xformedItem是对原始评分矩阵进行降维后的物品评分矩阵
    7.  
    8. def svdEst(userData,xformedItems,user,simMeas,item):
    9.     n = shape(xformedItems)[0]#用户数量
    10.     simTotal = 0.0 #初始化相似度的总和
    11.     ratSimTotal = 0.0 #初始化相似度及评分值的乘积（预测的评分）求和
    12.     #对给定的用户，for 循环所有物品，计算与item相似度
    13.     for j in range(n):
    14.        #每个物品的不同用户的评分
    15.         userRating = userData[:,j]
    16.         if userRating == 0 or j == item:
    17.             continue
    18.             #计算物品间的相似度
    19.         similarity = simMeas(xformedItems[item , :].T,xformedItems[j , :].T)
    20.         print('the %d and %d similarity is :%f' %(item,j,similarity))
    21.         #对相似度求和
    22.         simTotal += similarity
    23.         #对相似度及评分值的乘积求和
    24.         ratSimTotal += similarity*userRating
    25.  
    26.     if simTotal == 0 : 
    27.         return 0
    28.     else:
    29.         return ratSimTotal/simTotal

    对用户未评分过的物品进行预测 

    1.  
    2. #余弦相似度
    3. def cosSim(U_k,W_t):
    4.     num = float(U_k.T * W_t)
    5.     denom = linalg.norm(U_k)* linalg.norm(W_t)
    6.     return 0.5 + 0.5 * (num/denom)
    7.  
    8. # 寻找未评级的物品，对给定用户建立一个未评分的物品列表
    9. def recommend(dataMat,user,N = 3,simMeas = cosSim,estMethod = svdEst):
    10.     
    11.     U,Sigma,VT  = linalg.svd(dataMat)
    12.     #使用奇异值构建一个对角矩阵
    13.     Sig4 = mat(eye(4) * Sigma[:4])
    14.     #利用U矩阵将物品转换到低维空间中
    15.     xformedItem = dataMat.T * U[:,:4] * Sig4.I
    16.     print('xformedItem =',xformedItem)
    17.     print('xformedItem维度：',shape(xformedItem))
    18.     
    19.     unratedItems = nonzero(dataMat[user:].A==0)[1]#未评分的物品
    20.     print('dataMat[user:].A = ',dataMat[user:].A)
    21.     print('nonzero(dataMat[user:].A==0)结果为',nonzero(dataMat[user:].A==0))
    22.     #如果不存在未评分物品，退出函数，否则在所有未评分物品上进行循环
    23.     if len(unratedItems) == 0:
    24.         return ('you rated everyting')
    25.     itemScores = []
    26.     for item in unratedItems:
    27.         print('items = ',item)
    28.     #对于每个未评分物品，通过调用standEst() 来产生该物品基于相似度的预测评分
    29.         estimatedScore = estMethod(dataMat[user,:],xformedItem,user,simMeas,item)
    30.     #该物品的编号和估计得分值会放在一个元素列表itemScores
    31.         itemScores.append((item,estimatedScore))
    32.     #寻找前N个未评级物品
    33.     return sorted(itemScores,key = lambda jj:jj[1],reverse  = True)[:N]
    34.  
    35. myMat = mat(loadExData())
    36. result = recommend(myMat,1,estMethod = svdEst)
    37. print(result)

     流程总结：

    1. 加载用户对物品的评分矩阵
    2. 矩阵分解，求奇异值，根据奇异值的能量占比确定降维至k的数值
    3. 使用矩阵分解对物品评分矩阵进行降维
    4. 使用降维后的物品评分矩阵计算物品相似度，对用户未评分过得物品进行预测
    5. 产生前n个评分值高的物品，返回物品编号以及预测评分值 

    隐语义模型

    SVD计算前会把评分矩阵A的缺失值补全，补全之后的稀疏矩阵A表示成稠密矩阵，然后将A分解成A'= 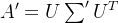A' = U\sum 'U^{T},这种方法有缺点：

    • 耗费巨大的存储空间，在实际中，用户对物品的行为信息何止千万，对这样的稠密矩阵进行存储是不现实的：
    • SVD的计算复杂度很高，更不用说这样的大规模稠密矩阵了。

    所以关于SVD的研究很多都是在小数据集上进行的。隐语义模型也是基于矩阵分解的，但是和SVD不同，它是把原始矩阵分解成两个矩阵相乘而不是三个。A=PQ^{T}

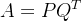
    现在的问题就变成了确定P和Q，我们把P叫作用户因子矩阵，Q叫作物品因子矩阵。通常上式不能达到精确相等的程度，我们要做的就是要最小化它们之间的差距，这又变成了一个最优化问题。通过优化损失函数来找到P和Q中合适的参数，其中行为用户i对物品j的评分。

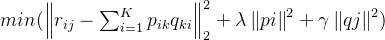    min(\left \| r_{ij}-\sum_{i = 1}^{K} p_{ik}q_{ki}\right \|_{2}^{2}+ \lambda \left \| pi \right \|^{2} +\gamma \left \| qj \right \|^{2} )       式一

    推荐系统中用户和物品的交互数据分为显性反馈和隐性反馈数据。隐式模型多了一个置信参数，这就涉及ALS中对于隐式反馈模型的处理方式——有的文章称为“加权的正则化矩阵分解”，它的损失函数如下：

    min(c_{ij}\left \| r_{ij}-\sum_{i = 1}^{K} p_{ik}q_{ki}\right \|_{2}^{2}+ \lambda \left \| pi \right \|^{2} +\gamma \left \| qj \right \|^{2} )式二

    隐式反馈模型中是没有评分的，所以在式子中Tij并不是具体分数，而仅为1，仅仅表示用户和物品之间有交互，而不表示评分高低或者喜好程度。函数中还有一个Cij的项，它 用来表示用户偏爱某个商品的置信程度，比如交互次数多的权重就会增加。如果我们用dij来表示交互次数的话，那么就可以把置信程度表示成如下公式：

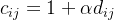
    c_{ij} = 1+\alpha d_{ij}

    这样，协同过滤就成功转化成了一个优化问题。为了求得以上损失函数最优解，最常用的是ALS算法，即交替最小二乘法（Alternating Least Squares）。算法的基础计算流程 是：

    （1）随机初始化Q，对式一中的Pi求偏导，令导数为0，得到当前最优解

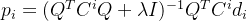
    p_{i} = (Q^{T}C^{i}Q +\lambda I)^{-1}Q^{T}C^{i}d_{i}

    2）固定p,对式一中的qj求偏导，令导数为0，得到当前最优解qj；

    3) 固定q,对式一中的pj求偏导，令导数为0，得到当前最优解pj；

    4)  循环2）和3），直到指定的迭代次数或收敛，对于大数据集，可以用spark进行ALS的计算

    实际问题中，由于待分解的矩阵通常非常稀疏，与SVD相比，ALS能有效地解决过拟合问题。基于ALS的矩阵分解的协同过滤算法的可拓展性也优于SVD。

  • 相关阅读:
    算法训练第五十八天
    推荐接口压测报告
    谷歌浏览器
    【17】c++设计模式——＞原型模式
    MySQL数据优化
    大规模场景下对Istio的性能优化
    DJ9-2 中断方式
    C语言之ASC转hex
    MySQL高级语句（一）
    Python_数据容器_字典
  • 原文地址：https://blog.csdn.net/m0_51933492/article/details/126647931