TinyRenderer学习笔记--Lesson 5

Lesson 5 移动相机

和第四节相似，这一节也会用到一些矩阵向量的计算，可以想象一下，我们在围绕一个物体进行环绕观察，物体在

世界坐标系中的位置是不会变化的，变化的是相机的位置。此时要正确的把图形渲染出来，需要重新计算物体和相

机之间的距离，重新进行投影计算，比较麻烦。所以相对的，我们把物体进行反操作，也能达到相同的效果。比如

相机围绕物体的y轴旋转，和物体绕着y轴反方向旋转，最后渲染出来的图形是一样的。

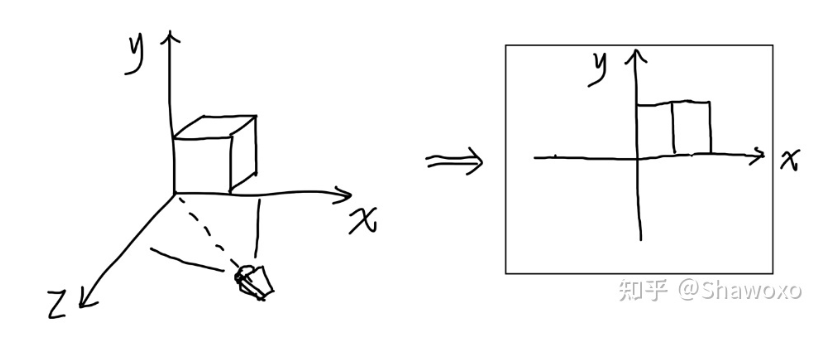
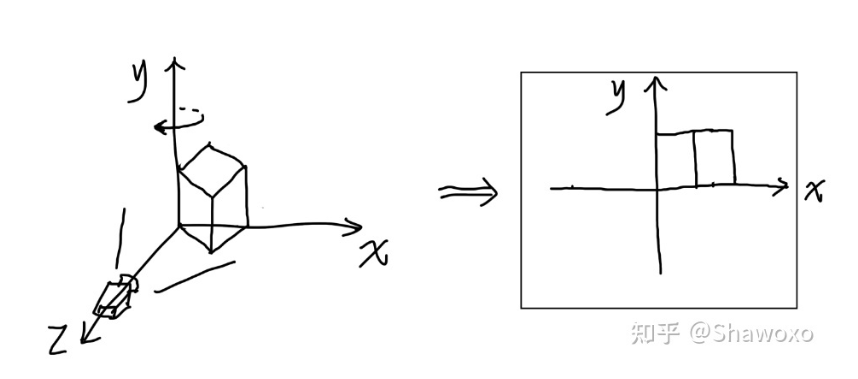
逆变换就对应着逆矩阵。

准备工作，在摄像机坐标系下，我们要引入up向量，它始终指向摄像机的上方，注意，这里的up是摄像机坐标系下的up。即下图中的Up direction向量。

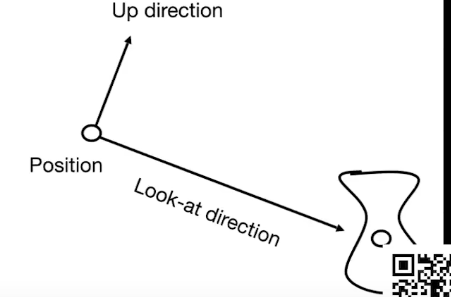
下面，需要把摄像机进行旋转，让摄像机的上方向指向世界坐标系的Y方向，摄像机的目标方向 (direction) 指向世界坐标系的 -Z 方向。

-direction方向比较好求，直接用摄像机的坐标(x,y,z) - (0,0,0)就能得到，这个就是新的坐标

系的Z轴。前面我们定义了up向量，up × Z = X，这样就得到了X轴，继而X × Z = Y，这样就得到了新的X,Y,Z轴。

矩阵表示为

这个就是把摄像机旋转到 ”摄像机的上方向指向世界坐标系的Y方向，摄像机的目标方向 (direction) 指向世界坐

**标系的 -Z 方向“**状态的矩阵。此时，摄像机依然看向物体，不过物体仍然在center位置，不在原点。

然后下一步，我们需要把看向的位置移动到世界坐标系的原点，看向的位置可以理解成物体的位置，因为我们最终

得到的场景是摄像机位于Z轴负方向的位置，看向原点，所以要把看向的位置移到原点，看向的位置我们定义成

center点。这个操作使用平移矩阵表示为

这就是摄像机的操作，先旋转，再平移，就能达到我们理想的状态。但是前面说过，我们要求得是摄像机不动，物体动，那就要求这两个矩阵的逆

现在，把这两个矩阵应用到物体上，就达到了摄像机移动的视觉效果。

这里和普通的属兔变换要注意区别，普通的视图变换是作用在摄像机上的，这里是作用在物体上的。games101里

面的视图变换是把摄像机移动到原点并看向-Z轴方向，这里是把物体移动到原点，摄像机在Z轴方向看向原点，之

后我会改代码，改成games101的那种，这个实在是不好理解，看了好半天！！！

Matrix lookat(Vec3f eye, Vec3f center, Vec3f up) {
    Vec3f z = (eye - center).normalize();
    Vec3f x = (up ^ z).normalize();
    Vec3f y = (z ^ x).normalize();
    Matrix res = Matrix::identity(4);
    for (int i = 0; i < 3; i++) {
        //旋转子矩阵
        res[0][i] = x[i];
        res[1][i] = y[i];
        res[2][i] = z[i];
        //平移子矩阵
        res[i][3] = -center[i];
    }
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

效果图：

这里图片更加平滑了，因为加入了高洛德着色法，原来我们使用的是平面着色，就是整个三角形平面使用一个方向

的法线，计算得到的光强是一样的，这样得到的效果就是整个三角形都是一种颜色，导致渲染出来的图片有明显的

条痕。高洛德着色是将三角形三个顶点的法向量都算出来，然后进行插值，这样三角形内部的颜色就是渐变的。

这里插值使用的线性插值，所以三角形的栅格化就是用的扫线法。

void triangle(Vec3i t0, Vec3i t1, Vec3i t2, float ity0, float ity1, float ity2, Vec2i uv0, Vec2i uv1, Vec2i uv2, float dis0, float dis1, float dis2, TGAImage& image, int* zbuffer) {
    //按照y分割为两个三角形
    if (t0.y == t1.y && t0.y == t2.y) return;
    if (t0.y > t1.y) { std::swap(t0, t1); std::swap(ity0, ity1); std::swap(uv0, uv1); }
    if (t0.y > t2.y) { std::swap(t0, t2); std::swap(ity0, ity2); std::swap(uv0, uv2); }
    if (t1.y > t2.y) { std::swap(t1, t2); std::swap(ity1, ity2); std::swap(uv1, uv2); }
    int total_height = t2.y - t0.y;
    for (int i = 0; i < total_height; i++) {
        bool second_half = i > t1.y - t0.y || t1.y == t0.y;
        int segment_height = second_half ? t2.y - t1.y : t1.y - t0.y;
        float alpha = (float)i / total_height;
        float beta = (float)(i - (second_half ? t1.y - t0.y : 0)) / segment_height;
        //计算A,B两点的坐标
        Vec3i A = t0 + Vec3f(t2 - t0) * alpha;
        Vec3i B = second_half ? t1 + Vec3f(t2 - t1) * beta : t0 + Vec3f(t1 - t0) * beta;
        //计算A,B两点的光照强度
        float ityA = ity0 + (ity2 - ity0) * alpha;
        float ityB = second_half ? ity1 + (ity2 - ity1) * beta : ity0 + (ity1 - ity0) * beta;
        //计算UV
        Vec2i uvA = uv0 + (uv2 - uv0) * alpha;
        Vec2i uvB = second_half ? uv1 + (uv2 - uv1) * beta : uv0 + (uv1 - uv0) * beta;
        //计算距离
        float disA = dis0 + (dis2 - dis0) * alpha;
        float disB = second_half ? dis1 + (dis2 - dis1) * beta : dis0 + (dis1 - dis0) * beta;
        if (A.x > B.x) { std::swap(A, B); std::swap(ityA, ityB); }
        //x坐标作为循环控制
        for (int j = A.x; j <= B.x; j++) {
            float phi = B.x == A.x ? 1. : (float)(j - A.x) / (B.x - A.x);
            //计算当前需要绘制点P的坐标，光照强度
            Vec3i    P = Vec3f(A) + Vec3f(B - A) * phi;
            float ityP = ityA + (ityB - ityA) * phi;
            ityP = std::min(1.f, std::abs(ityP) + 0.01f);
            Vec2i uvP = uvA + (uvB - uvA) * phi;
            float disP = disA + (disB - disA) * phi;
            int idx = P.x + P.y * width;
            //边界限制
            if (P.x >= width || P.y >= height || P.x < 0 || P.y < 0) continue;
            if (zbuffer[idx] < P.z) {
                zbuffer[idx] = P.z;
                TGAColor color = model->diffuse(uvP);
                image.set(P.x, P.y, TGAColor(color.bgra[2], color.bgra[1], color.bgra[0]) * ityP * (20.f / std::pow(disP, 2.f)));
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45