LeetCode刷题（12）

树相关题目

104. Maximum Depth of Binary Tree (Easy)

问题描述
给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。

代码

public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
    }
1
2
3
4

110. Balanced Binary Tree (Easy)

问题描述
给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

思路
如果一个节点为空，则返回true；
如果一个节点左子和右子深度只差大于1，返回false；
遍历其他的结点，当所有节点都为平衡时，即为平衡二叉树返回true。

代码

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root == null) return true;
        if(Math.abs(maxDepth(root.left)-maxDepth(root.right))>1){
            return false;
        }
        return isBalanced(root.left) && isBalanced(root.right);
    }
    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

543. Diameter of Binary Tree (Easy)

问题描述
给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :
给定二叉树

      1
     / \
    2   3
   / \     
  4   5    
1
2
3
4
5

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

思路
如果root为空，则返回0；否则计算左子和右子的深度之和即为直径，遍历所有节点，找到最大的直径。

代码

class Solution {
    public int diameterOfBinaryTree(TreeNode root) {
        if(root == null) return 0;
        int max = maxDepth(root.left)+maxDepth(root.right);
        int left = diameterOfBinaryTree(root.left);
        int right = diameterOfBinaryTree(root.right);
        max = Math.max(max,left);
        max = Math.max(max,right);
        return max;
    }

    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

437. Path Sum III (Easy)

问题描述
给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

思路
从根节点向下递归遍历每个节点，遍历节点时使用一个辅助统计函数统计从当前节点向下出发有多少个满足条件的路径。

辅助统计函数的逻辑是，如果当前根节点的值等于目标值，则说明已经统计到了一个满足条件的情况。然后分别从左子和右子出发找目标值为target-root.val的情况有多少种。

代码

class Solution {
    public int pathSum(TreeNode root, int targetSum) {
        if(root == null) return 0;
        int count = countPath(root,targetSum);
        count+= pathSum(root.left,targetSum);
        count+= pathSum(root.right,targetSum);
        return count;
    }

	//辅助函数，统计从当前位置出发有多少路径和为target的情况
    public int countPath(TreeNode root,long targetSum){
        int count=0;
        if(root == null)return 0;
        if(root.val == targetSum) count++;
        count+=countPath(root.left,targetSum-root.val);
        count+=countPath(root.right,targetSum-root.val);
        return count;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

101. Symmetric Tree (Easy)

问题描述
给你一个二叉树的根节点 root ， 检查它是否轴对称。

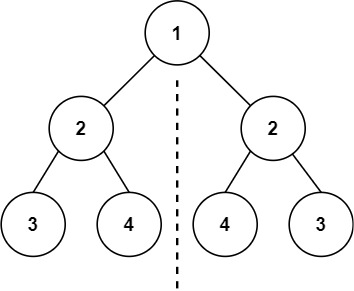
思路
如果根节点为空，则返回true；
使用两个指针分别指向根节点的左右节点，使用一个辅助函数判断这两个对称位置的指针指向的值是否一致。

辅助函数的逻辑：
如果两个指针指向的值一个为空另一个不为空，则不对称；
如果两个都为空，则算对称；
如果两个都不为空，进一步判断对应的值是否相等，不相等则不对称，相等则向后递归遍历做进一步判断。

代码

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null)return true;
        return isSymmetricHelp(root.left,root.right);
    }
    public boolean isSymmetricHelp(TreeNode left,TreeNode right){
        if(left == null && right == null)return true;
        if(left == null || right == null)return false;
        if(left.val != right.val)return false;
        return isSymmetricHelp(left.left,right.right)&&isSymmetricHelp(left.right,right.left);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

637. Average of Levels in Binary Tree (Easy)

问题描述
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。

思路
层次遍历，使用一个队列来实现，在遍历过程中累加同一层的节点值并求平均。

代码

class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        Deque<TreeNode> queue = new LinkedList<>();
        List<Double> result = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()){
            int n = queue.size();
            double s = 0;
            for(int i=0;i<n;i++){
                TreeNode tem = queue.poll();
                s += tem.val;
                if(tem.left!=null){
                    queue.offer(tem.left);
                }
                if(tem.right!=null){
                    queue.offer(tem.right);
                }
            }
            result.add(s/n);
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

105. Construct Binary Tree from Preorder and Inorder Traversal (Medium)

问题描述
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

思路
先序遍历的第一个节点一定是根节点，于是可以把中序遍历中的数组分为两个部分，左边的部分和先序遍历前面的一部分数组可以通过递归调用该函数生成左子，右边的部分和先序遍历后面的一部分数组可以通过递归调用该函数生成右子。

代码

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder.length == 0 || inorder.length == 0) return null;
        TreeNode root = null;

        for(int j=0;j<inorder.length;j++){
            if(preorder[0]==inorder[j]){
                int[] left = Arrays.copyOfRange(inorder,0,j);
                int[] right = Arrays.copyOfRange(inorder,j+1,inorder.length);

                int[] newPreOrder_l = Arrays.copyOfRange(preorder,1,1+j);//同样向后找j个作为左子新preOrder
                int[] newPreOrder_r = Arrays.copyOfRange(preorder,1+j,preorder.length);//后面j个作为右子新preOrder

                root = new TreeNode(preorder[0]);
                root.left = buildTree(newPreOrder_l,left);
                root.right = buildTree(newPreOrder_r,right);
            }
        }
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

144. Binary Tree Preorder Traversal (Medium)

问题描述
给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

思路
非递归版，可以使用一个栈，每个节点如果不为空则可以入栈，每次出栈时保存结果。需要注意的是，先右子入栈，再左子入栈，才能保证先序遍历的顺序。

代码

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<>();
        List<Integer> result = new LinkedList<>();
        if(root==null)return result;
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode pop = stack.pop();
            result.add(pop.val);
            if(pop.right!=null){
                stack.push(pop.right);
            }
            if(pop.left!=null){
                stack.push(pop.left);
            }
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

669. Trim a Binary Search Tree (Easy)

问题描述
给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

输入输出样例
示例 1：

示例 2：

思路
二叉查找树的特点，右子树大于根节点，左子树小于根节点。所以遍历一个节点时，如果根节点大于high则删除根节点以及右子；如果根节点小于low则删除根节点以及左子。如果在范围内，则保存根节点，分别遍历左子和右子节点。

代码

class Solution {
	//函数功能为删除不在范围的节点，然后返回新树的头结点
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if(root == null) return null;
        if(root.val>high){//当前节点大于最大值，应当删除当前节点和右边的子节点，然后遍历下一个节点
            return trimBST(root.left,low,high);//从root.left开始遍历，则相当于删除了头结点和右子
        }
        if(root.val<low){//当前节点小于最小值，应当删除当前节点和左边的子节点，然后遍历下一个节点
            return trimBST(root.right,low,high);
        }
        //如果在范围内，保留根节点，遍历下一个节点
        root.left = trimBST(root.left,low,high);
        root.right = trimBST(root.right,low,high);
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

208. Implement Trie (Prefix Tree) (Medium)

问题描述
Trie 或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

思路
前缀树可以看做一个由26个子分支的树，如果某个字母存在，则该单词对应的分支不为空。

插入单词操作：从根节点开始遍历前缀树，同时遍历单词中的每个字母，如果该字母不存在，则为该结点的该字母分支创建一个新的节点；如果存在则不创建。完全插入该字母后，将该位置节点的isVal标记为true。

查找单词操作：从根节点按照字母路径查找，如果该路径存在，且最后一个节点的isVal为true，则存在该单词，如果路径不存在，或者最后一个节点的isVal为false，说明该单词不存在。

前缀查找：从根节点按照字母路径查找，如果该路径存在则返回true，否则为false。

代码

//定义结点的数据结构
class TrieNode{
    TrieNode[] nodes; //next节点数组
    boolean isVal; //保存该结点是否是某单词的最后一个节点

    TrieNode(){
        nodes = new TrieNode[26];
        for (int i = 0; i < 26; i++) {
            nodes[i]=null;
        }
        isVal = false;
    }
}
//前缀树的数据结构
class Trie {
    TrieNode root;
    public Trie() {
        root = new TrieNode();
    }

    public void insert(String word) {
        TrieNode p = root;
        for(char ch:word.toCharArray()){
            if(p.nodes[ch-'a']==null){
                p.nodes[ch-'a']=new TrieNode();
            }
            p = p.nodes[ch-'a'];
        }
        p.isVal = true; //在这条路径的最后一个节点处标记其是一个单词
    }

    public boolean search(String word) {
        TrieNode p = root;
        for(char ch:word.toCharArray()){
            if(p.nodes[ch-'a']==null){
                return false;
            }
            p = p.nodes[ch-'a'];
        }
        return p.isVal;//存在这条路径，然后看最后一个节点的isVal判断是否是一个单词
    }

    public boolean startsWith(String prefix) {
        TrieNode p = root;
        for(char ch:prefix.toCharArray()){
            if(p.nodes[ch-'a']==null){
                return false;
            }
            p = p.nodes[ch-'a'];
        }
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

Invert Binary Tree (Easy)

问题描述
给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

思路
如果根节点不为空，首先交换两个子节点。然后递归对左子和右子进行交换。

代码

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null)return null;
        TreeNode tem = root.left;
        root.left = root.right;
        root.right = tem;
        root.left = invertTree(root.left);
        root.right = invertTree(root.right);
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11

617. Merge Two Binary Trees (Easy)

问题描述
给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

输入输出样例
示例 1：

思路
如果两个节点都为空，则返回空；
如果两个节点一个为空，则返回另外一个节点；
如果两个都不为空，则创建一个新的节点，节点值为两个节点值之和。
然后根节点的左右子，分别指向两个节点后继左右子节点的递归遍历。

代码

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null && root2==null) return null;
        if(root1 == null) return root2;
        if(root2 == null) return root1;
        TreeNode root = new TreeNode(root1.val+root2.val);
        root.left = mergeTrees(root1.left,root2.left);
        root.right = mergeTrees(root1.right,root2.right);
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11

572. Subtree of Another Tree (Easy)

问题描述
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

思路
使用一个辅助函数判断两棵树是否完全一样，之后遍历主树，从每个节点开始和子树使用辅助函数比较，如果相同则返回true，如果不同则用下一个节点和子树比较，如果从所有节点开始和子树比较都不相同，则返回false。递归的出口在于：如果主树结点为空，子树节点不为空，则返回false。

代码

class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root == null && subRoot == null) return true;
        if(root == null) return false; //递归出口，如果主树为空，子树不为空，则返回false
        if(subRoot == null) return true;
        //根节点，左子树，右子树分别与模板树比较，只要有一个完全相同则存在子树，返回true.
        return isSame(root,subRoot) || isSubtree(root.left,subRoot) || isSubtree(root.right,subRoot);
    }
    
    public boolean isSame(TreeNode root,TreeNode subRoot){
        if(root == null && subRoot == null) return true; //都为空
        if(root == null || subRoot == null) return false; //其中一个为空
        if(root.val!=subRoot.val)return false;
        return isSame(root.left,subRoot.left)&&isSame(root.right,subRoot.right);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

404. Sum of Left Leaves (Easy)

问题描述
给定二叉树的根节点 root ，返回所有左叶子之和。

输入输出样例
示例 1：

输入: root = [3,9,20,null,null,15,7]

输出: 24
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

思路
使用一个辅助函数判断当前节点是否为叶子节点，如果为叶子节点时则返回其节点值，否则为0。主函数中每次将左节点放入辅助函数中统计，然后递归遍历所有节点。

代码

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if(root == null)return 0;
        int sum = 0;
        if(root.left == null && root.right ==null)return 0;
        sum+=leftLeaf(root.left);
        sum+=sumOfLeftLeaves(root.left);
        sum+=sumOfLeftLeaves(root.right);
        return sum;
    }

    public int leftLeaf(TreeNode root){
        if(root == null)return 0;
        if(root.left == null &&root.right == null) return root.val;
        return 0;
    }
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

513. Find Bottom Left Tree Value (Easy)

问题描述
给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

输入输出样例
示例 1:

输入: root = [2,1,3]
输出: 1

示例 2:

输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

思路
最下层的最左侧节点，就是层次遍历最后一层的第一个节点。使用一个result保存每层遍历时第一个访问的节点值，这样所有层遍历完之后，result就是最终需要的结果。

代码

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int result=0;
        while (!queue.isEmpty()){
            int len = queue.size();
            for (int i = 0; i < len; i++) {
                TreeNode tem = queue.poll();
                if(i == 0) result = tem.val;
                if(tem.left!=null){
                    queue.offer(tem.left);
                }
                if(tem.right!=null){
                    queue.offer(tem.right);
                }
            }
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

538. Convert BST to Greater Tree (Easy)

问题描述
给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

输入输出样例
示例 1：

输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

思路
仔细观察不难发现，该累加数其实每个节点值是按照右-根-左的顺序遍历二叉树然后累加上一个节点的结果得到的。于是可以使用一个全局变量pre保存上一次访问的累加树的节点值。

代码

class Solution {
    private int pre=0;
    public TreeNode convertBST(TreeNode root) {
        if(root == null)return null;
        root.right = convertBST(root.right);
        root.val += pre; //将当前节点的值加上上一个累加树结点值
        pre = root.val; //更新pre
        root.left = convertBST(root.left);
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11

235. Lowest Common Ancestor of a Binary Search Tree (Easy)

问题描述
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

输入输出样例
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。

思路
二叉搜索树的特点是，大于根节点的节点在右子中，小于根节点的节点在左子中。当根节点的值正好在p和q中间时，其为最近的公共祖先。否则去相应的左子或者右子树中查找。

代码

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null) return null;
        int big = Math.max(p.val,q.val);
        int small = Math.min(p.val,q.val);
        if(root.val>big){
            return lowestCommonAncestor(root.left,p,q);
        }
        if(root.val<small){
            return lowestCommonAncestor(root.right,p,q);
        }
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

530. Minimum Absolute Difference in BST (Easy)

问题描述
给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数，其数值等于两值之差的绝对值。

思路
利用中序遍历，这样结果就是有序的，只要求最小的两个相邻数之差的绝对值即可。

代码

class Solution {
    public int getMinimumDifference(TreeNode root) {
        int min = Integer.MAX_VALUE/2;
        int pre = Integer.MAX_VALUE/2;
        LinkedList<Integer> list = new LinkedList<>();
        minTravel(root,list);
        for(int a:list){
            min = Math.min(min,Math.abs(a-pre));
            pre = a;
        }
        return min;
    }
    
    public void minTravel(TreeNode root,List<Integer> list){
        if(root == null)return;
        minTravel(root.left,list);
        list.add(root.val);
        minTravel(root.right,list);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

889. Construct Binary Tree from Preorder and Postorder Traversal (Medium)

问题描述
给定两个整数数组，preorder 和 postorder ，其中 preorder 是一个具有 无重复 值的二叉树的前序遍历，postorder 是同一棵树的后序遍历，重构并返回二叉树。

如果存在多个答案，您可以返回其中 任何 一个。

思路
前序遍历为：

(根结点) (前序遍历左分支) (前序遍历右分支)
1

而后序遍历为：

(后序遍历左分支) (后序遍历右分支) (根结点)
1

前序遍历数组的开头和后续遍历数组的结尾相同，为当前树的根节点。然后我们需要找到两个遍历数组的剩余数组左右分支中心。
使用一个例子说明找到数组分开的中心：

例如，如果最终的二叉树可以被序列化的表述为 [1, 2, 3, 4, 5, 6, 7]，那么其前序遍历为 [1] + [2, 4, 5] + [3, 6, 7]，而后序遍历为 [4, 5, 2] + [6, 7, 3] + [1]。前序遍历中pre[1]在后序遍历中的位置+1就为分开的位置。

代码

class Solution {
    public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
        int n = preorder.length;
        if(n == 0)return null;
        TreeNode root = new TreeNode(preorder[0]);
        int j=0;
        for(int i=0;i<n-1;i++){
            if(preorder[1]==postorder[i]){
                j = i+1;//找到分成两部分的位置
                break;
            }
        }
        int[] preOrder_l = Arrays.copyOfRange(preorder,1,1+j);
        int[] preOrder_r = Arrays.copyOfRange(preorder,1+j,n);
        int[] postOrder_l = Arrays.copyOfRange(postorder,0,j);
        int[] postOrder_r = Arrays.copyOfRange(postorder,j,n-1);
        root.left = constructFromPrePost(preOrder_l,postOrder_l);//生成左子树
        root.right = constructFromPrePost(preOrder_r,postOrder_r);//生成右子树
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

106. Construct Binary Tree from Inorder and Postorder Traversal (Medium)

问题描述
给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

思路
后续遍历的最后一个元素是根节点，将中序遍历的结果一分为二，左侧为左子树，右侧为右子树，再将后序遍历也划分为两部分。之后分别再构建左子和右子树。

代码

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        int n = inorder.length;
        if(n == 0)return null;
        TreeNode root = new TreeNode(postorder[n-1]);
        int j=0;
        for(int i=0;i<n;i++){
            if(inorder[i]==postorder[n-1]){
                j = i;
                break;
            }
        }
        int[] inorder_l = Arrays.copyOfRange(inorder,0,j);
        int[] inorder_r = Arrays.copyOfRange(inorder,j+1,n);
        int[] postorder_l = Arrays.copyOfRange(postorder,0,j);
        int[] postorder_r = Arrays.copyOfRange(postorder,j,n-1);
        root.left = buildTree(inorder_l,postorder_l);
        root.right = buildTree(inorder_r,postorder_r);
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

94. Binary Tree Inorder Traversal (Medium)

问题描述
给定一个二叉树的根节点 root ，返回 它的中序遍历 。（使用非递归）

思路
和先序遍历类似，都是使用栈来完成的。区别是，先序遍历是先访问在进堆，中序遍历是先进栈，出栈再访问。

代码

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<>();
        LinkedList<Integer> result = new LinkedList<>();
        if(root == null)return result;
        TreeNode p = root;
        do {
            if(p!=null){
                stack.push(p);
                p = p.left;
            }else {
                p = stack.pop();
                result.add(p.val);
                p = p.right;
            }
        }while (p!=null||!stack.isEmpty());//p没有为空或者栈没有空都继续执行
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

145. Binary Tree Postorder Traversal (Medium)

问题描述
给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。(非递归)

思路
后续遍历->左-右-根，其实可以看作是先序遍历根-右-左的结果的倒叙结果。这里使用一个双向链表存储结果，每次遍历的结果插在前面就完成了倒叙。

代码

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<>();
        LinkedList<Integer> result = new LinkedList<>();
        if(root == null) return result;
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode tem = stack.pop();
            result.offerFirst(tem.val);
            if(tem.left!=null){
                stack.push(tem.left);
            }
            if(tem.right!=null){
                stack.push(tem.right);
            }
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

代码二

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        Deque<TreeNode> stack = new LinkedList<>();
        LinkedList<Integer> result = new LinkedList<>();
        if(root == null) return result;
        TreeNode p = root;
        while (p!=null || !stack.isEmpty()){
            if(p!=null){
                result.offerFirst(p.val);
                stack.push(p);
                p = p.right;
            }else {
                p = stack.pop();
                p = p.left;
            }
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

897. Increasing Order Search Tree (Easy)

问题描述
给你一棵二叉搜索树的 root ，请你 按中序遍历 将其重新排列为一棵递增顺序搜索树，使树中最左边的节点成为树的根节点，并且每个节点没有左子节点，只有一个右子节点。

输入输出样例
示例 1：

思路
中序遍历，然后每次访问头结点的时候，将头结点放在新树的右子节点上。

代码

class Solution {
    TreeNode newRoot =  new TreeNode(-1); 
    TreeNode p = newRoot; //p指针要不受每次循环的影响，于是可以作为全局变量或者作为参数进行传递
    public TreeNode increasingBST(TreeNode root) {
        travel(root);
        return newRoot.right;
    }

    public void travel(TreeNode root){
        if(root == null)return;
        travel(root.left);
        p.right = new TreeNode(root.val);
        p.left = null;
        p = p.right;
        travel(root.right);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

653. Two Sum IV - Input is a BST (Easy)

问题描述
给定一个二叉搜索树 root 和一个目标结果 k，如果二叉搜索树中存在两个元素且它们的和等于给定的目标结果，则返回 true。

输入输出样例

思路
可以借鉴一个数组中是否存在两个数之和为某值那一题的思路。用一个哈希表记录已将遍历过的值，然后在遍历某个值时看tartget-k是否在哈希表中。

代码

class Solution {
    Set<Integer> set = new HashSet<>();
    public boolean findTarget(TreeNode root, int k) {
        if(root == null)return false;
        if(set.contains(k-root.val)) return true;
        set.add(root.val);
        return findTarget(root.left,k) || findTarget(root.right,k);
    }
}
1
2
3
4
5
6
7
8
9

236. Lowest Common Ancestor of a Binary Tree (Medium)

问题描述
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

思路
若 root是 p,q 的 最近公共祖先 ，则只可能为以下情况之一：

p 和 q 在 root 的子树中，且分列 root 的 异侧（即分别在左、右子树中）；
p=root ，且 q 在 root 的左或右子树中；
q=root ，且 p 在 root 的左或右子树中；

代码

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null || root==p || root==q)return root;
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if(left == null)return right;
        if(right == null)return left;
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10

109. Convert Sorted List to Binary Search Tree (Medium)

问题描述
给定一个单链表的头节点 head ，其中的元素 按升序排序 ，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。

思路
改题可构造的平衡二叉树有多种，只要满足条件即可。这里采用二分法来构造，由于链表本身有序，从中间节点开始将链表分成两部分，使用这两部分分别递归构造左子和右子树一定是平衡的二叉树。链表找重中可以使用快慢指针。删除中间节点的时候需要考虑该指针如果是某个子链表的头结点，应该具体怎么删除。

代码

class Solution {
    public TreeNode sortedListToBST(ListNode head) {
        if(head == null)return null;
        ListNode fast = head.next;
        ListNode slow = head;
        ListNode pre = null; //使用pre作为待删除中点节点的前驱结点
        while (fast!=null && fast.next!=null){
            fast = fast.next.next;
            pre = slow;
            slow = slow.next;
        }
        //fast指针走到结尾时，slow指针正好为链表中点
        fast = slow.next;//fast重新指向右边链表的头
        if(pre == null){ //需要考虑slow为头结点时删除slow结点
            head = null; //直接将左边链表的长度变为0
        }else{
            pre.next = null; //删除slow指向的中间结点
        }
        
        TreeNode root = new TreeNode(slow.val);
        root.left = sortedListToBST(head);
        root.right = sortedListToBST(fast);
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

450. Delete Node in a BST (Medium)

问题描述
给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

输入输出样例

思路
着重讨论最复杂的情况，即删除的key正好为某个子树的root结点，且当前root结点左右子都不为空：
若左右子树均不为空，我们有两种选择：

从「当前节点的左子树」中选择「值最大」的节点替代 root 的位置，确保替代后仍满足 BST 特性；
从「当前节点的右子树」中选择「值最小」的节点替代 root 的位置，确保替代后仍满足 BST 特性；
我们以「从当前节点的左子树中选择值最大的节点」为例子，我们通过树的遍历，找到其位于「最右边」的节点，记为 t（t 作为最右节点，必然有 t.right = null），利用原本的 root 也是合法 BST，原本的 root.right 子树的所有及节点，必然满足大于 t.val，我们可以直接将 root.right 接在 t.right 上，并返回我们重接后的根节点，也就是 root.left。

代码（1）

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root == null)return null;
        if(root.val != key){
            if(root.val>key) root.left = deleteNode(root.left,key);
            else  root.right = deleteNode(root.right,key);
            return root;
        }else {
            if(root.left == null)return root.right;
            if(root.right == null)return root.left;
            //相等，且左右子都不为空的情况
            TreeNode right = root.left;
            while (right.right!=null)right=right.right;
            right.right = root.right;
            return root.left;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

代码（2）

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root == null)return null;
        if(root.val != key){
            if(root.val>key) root.left = deleteNode(root.left,key);
            else  root.right = deleteNode(root.right,key);
            return root;
        }else {
            if(root.left == null)return root.right;
            if(root.right == null)return root.left;
            //相等，且左右子都不为空的情况
            TreeNode left = root.right;
            while (left.left!=null) left=left.left;
            left.left = root.left;
            return root.right;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

说明：代码（1）和代码（2）分别是左子树最右侧结点代替根节点，和右子树最左侧结点代替根节点的样例。