【机器学习】解决过拟合、ReLU激活函数

本文目录

• 1. 什么是过拟合？
• 2. 解决过拟合的方法
• • 方法一：增加数据量
  • 方法二：运用正规化
  • • Dropout（正规化方法）
  • 方法三：简化模型
  • 方法四：多种模型组合
  • • 1. Bagging
    • 2. Boosting
    • 3. Dropout
• 3. 激活函数之ReLU函数
• • 使用Relu函数有什么优势？

参考资料：

• 过拟合内容来源知乎 https://zhuanlan.zhihu.com/p/266658432
• ReLU函数内容来源简书 https://www.jianshu.com/p/338afb1389c9

1. 什么是过拟合？

过拟合 = 过度自信 = 自负
Overfitting 也被称为过度学习，过度拟合。 它是机器学习中常见的问题。 举个Classification（分类）的例子。

尽管overfitting模型的曲线很精确的区分了所有的训练数据，但是并没有描述数据的整体特征，对新测试数据的适应性较差。

2. 解决过拟合的方法

方法一：增加数据量

大部分过拟合产生的原因是因为数据量太少了. 如果我们有成千上万的数据, 红线也会慢慢被拉直, 变得没那么扭曲 .

1. 从数据源头获得更多数据：多拍点照片等。

2. 数据增强（data augmentation）：通过一定规则来扩充数据，比如旋转，平移，亮度，切割等手段一张图片得到多张。 （一般图像处理会使用数据增加）

方法二：运用正规化

L1, l2 regularization等等, 这些方法适用于大多数的机器学习, 包括神经网络. 他们的做法大同小异, 我们简化机器学习的关键公式为 y=Wx . W为机器需要学习到的各种参数. 在过拟合中, W 的值往往变化得特别大或特别小. 为了不让W变化太大, 我们在计算误差上做些手脚.
原始的 cost 误差是这样计算, cost = 预测值-真实值的平方. 如果 W 变得太大, 我们就让 cost 也跟着变大, 变成一种惩罚机制. 所以我们把 W 自己考虑进来. 这里 abs 是绝对值. 这一种形式的 正规化, 叫做 l1 正规化.
L2 正规化和 l1 类似, 只是绝对值换成了平方. 其他的l3, l4 也都是换成了立方和4次方等等. 形式类似. 用这些方法,我们就能保证让学出来的线条不会过于扭曲。
（总结：让大参数的loss增大以惩罚）

Dropout（正规化方法）

专门用在神经网络的正规化的方法, 叫作 dropout。
在训练的时候, 我们随机忽略掉一些神经元和神经联结 , 是这个神经网络变得”不完整”. 用一个不完整的神经网络训练一次。
到第二次再随机忽略另一些, 变成另一个不完整的神经网络. 有了这些随机 drop 掉的规则, 我们可以想象其实每次训练的时候, 我们都让每一次预测结果都不会依赖于其中某部分特定的神经元。
像l1, l2正规化一样, 过度依赖的 W , 也就是训练参数的数值会很大, l1, l2会惩罚这些大的 参数。Dropout 的做法是从根本上让神经网络没机会过度依赖。

（总结：随机忽略某些神经元，用不完整的神经网络训练）

方法三：简化模型

Dropout 会随机删除一些神经元，以在不同批量上训练不同的神经网络架构。

过拟合主要是有两个原因造成的：数据太少+模型太复杂。

我们可以通过使用合适复杂度的模型来防止过拟合问题，让其足够拟合真正的规则，同时又不至于拟合太多抽样误差。

对于神经网络而言，我们可以从以下四个方面来限制网络能力：

1. 网络结构（Architecture）： 减少隐藏层，神经元个数。
2. 训练时间（Early stopping）： 因为我们在初始化网络的时候一般都是初始为较小的权值。训练时间越长，部分网络权值可能越大。如果我们在合适时间停止训练，就可以将网络的能力限制在一定范围内。
3. 限制权值（weight-decay）= 正规化（regularization）： 原理与训练时间一样，但是这类方法直接将权值的大小加入到 Cost 里，在训练的时候限制权值变大。以 L2 regularization为例：

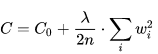
训练过程需要降低整体的 Cost，这时候，一方面能降低实际输出与样本之间的误差 ，也能降低权值大小。
4. 增加噪声（noise）： 在输入中加噪声（噪声会随着网络传播，按照权值的平方放大，并传播到输出层，对误差 Cost 产生影响。）在权值上加噪声。

方法四：多种模型组合

训练多个模型，以每个模型的平均输出作为结果。
从 N 个模型里随机选择一个作为输出的期望误差，会比所有模型的平均输出的误差大。

1. Bagging

简单理解，就是分段函数的概念：用不同的模型拟合不同部分的训练集。 以随机森林（Rand Forests）为例，就是训练了一堆互不关联的决策树。但由于训练神经网络本身就需要耗费较多自由，所以一般不单独使用神经网络做Bagging。

2. Boosting

既然训练复杂神经网络比较慢，那我们就可以只使用简单的神经网络（层数、神经元数限制等）。通过训练一系列简单的神经网络，加权平均其输出。

3. Dropout

这是一个很高效的方法。 在训练时，每次随机（如50%概率）忽略隐层的某些节点；这样，我们相当于随机从$2^H$个模型中采样选择模型；同时，由于每个网络只见过一个训练数据（每次都是随机的新网络），所以类似 bagging 的做法，这就是我为什么将它分类到「结合多种模型」中；

此外，而不同模型之间权值共享（共同使用这 H 个神经元的连接权值），相当于一种权值正则方法，实际效果比 L2 regularization 更好。

3. 激活函数之ReLU函数

首先，relu函数是常见的激活函数中的一种，表达形式如下：
$$f(x)=max(0,x)$$
ReLU函数的图像和求导后图像如下：

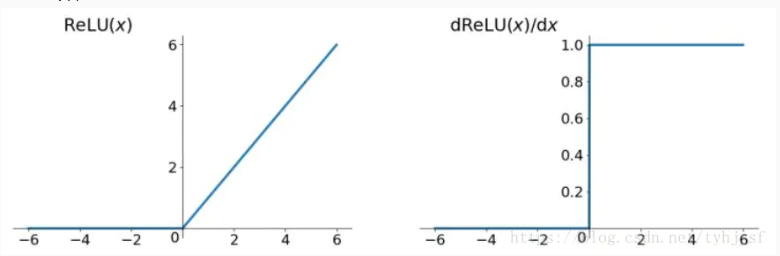
从表达式和图像可以明显地看出：Relu其实就是个取最大值的函数。
ReLU函数其实是分段线性函数，把所有的负值都变为0，而正值不变，这种操作被成为单侧抑制。

（也就是说：在输入是负值的情况下，它会输出0，那么神经元就不会被激活。这意味着同一时间只有部分神经元会被激活，从而使得网络很稀疏，进而对计算来说是非常有效率的。 ）正因为有了这单侧抑制，才使得神经网络中的神经元也具有了稀疏激活性。尤其体现在深度神经网络模型(如CNN)中，当模型增加N层之后，理论上ReLU神经元的激活率将降低2的N次方倍。

为什么要神经元稀疏？ 暂时不清楚，如果有大佬知道，请告诉我一下！

使用Relu函数有什么优势？

1.没有饱和区，不存在梯度消失问题。
2.没有复杂的指数运算，计算简单、效率提高。
3.实际收敛速度较快，比 Sigmoid/tanh 快很多。
4.比 Sigmoid 更符合生物学神经激活机制。

当然relu也存在不足： 就是训练的时候很”脆弱”，很容易就”die”了。举个例子：一个非常大的梯度流过一个 ReLU 神经元，更新过参数之后，这个神经元再也不会对任何数据有激活现象了。如果这个情况发生了，那么这个神经元的梯度就永远都会是0。实际操作中，如果你的learning rate 很大，那么很有可能你网络中的40%的神经元都”dead”了。 当然，如果你设置了一个合适的较小的learning rate，这个问题发生的情况其实也不会太频繁。（一句话总结，如果学习率太大会导致神经元梯度变0的概率变高，而小学习率不会导致这个问题。）