-
算法学习笔记 4-1 二分算法(Binary-Search):致敬经典,超越经典 与 LeetCode真题(Java)
喜欢该类型文章可以给博主点个关注,博主会持续输出此类型的文章,知识点很全面,再加上LeetCode的真题练习,每一个LeetCode题解我都写了详细注释,比较适合新手入门数据结构与算法,后续也会更新进阶的文章。
课件参考—开课吧《门徒计划》4-1 二分算法(Binary-Search):致敬经典,超越经典
二分算法基础知识
使用二分算法需要有一个基础:必须在有序的数据集合中,才可以使用二分算法。
我们常说的二分算法是一个大类,只要每次操作能把数据规模缩小到原来的一半,我们都管它叫做二分算法,它是一种思维方式。
二分查找
二分查找是二分算法的一个子类,是二分思想的一个具体的算法。
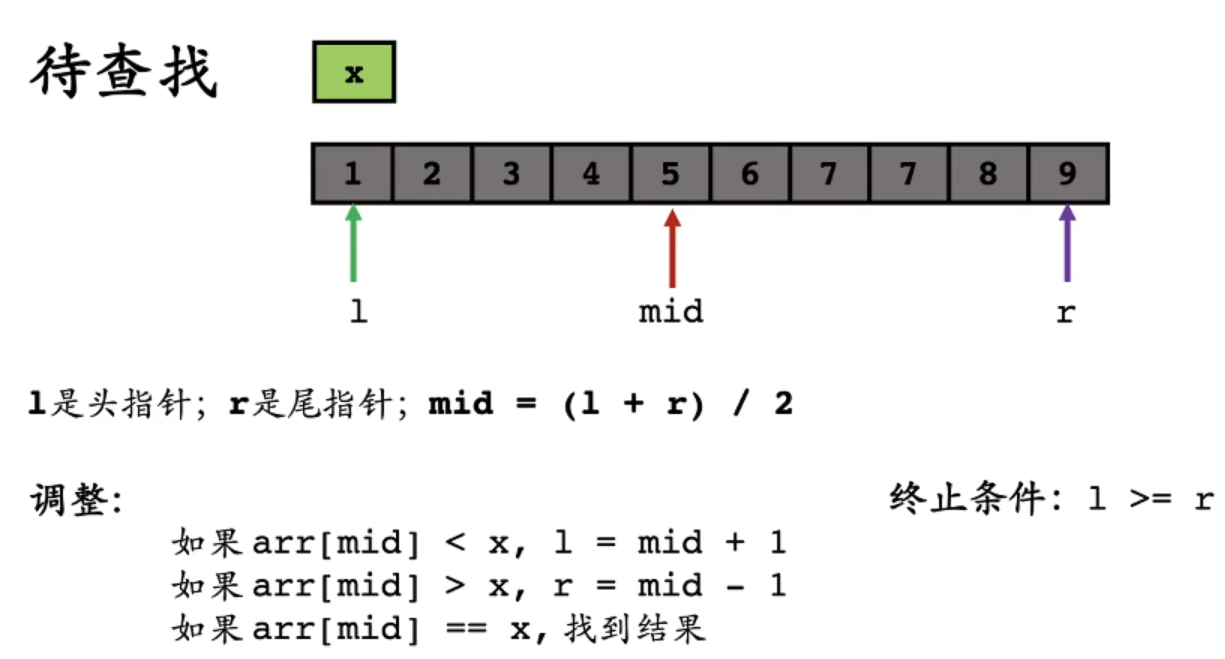
假设我们要找的数字为 4 4 4:
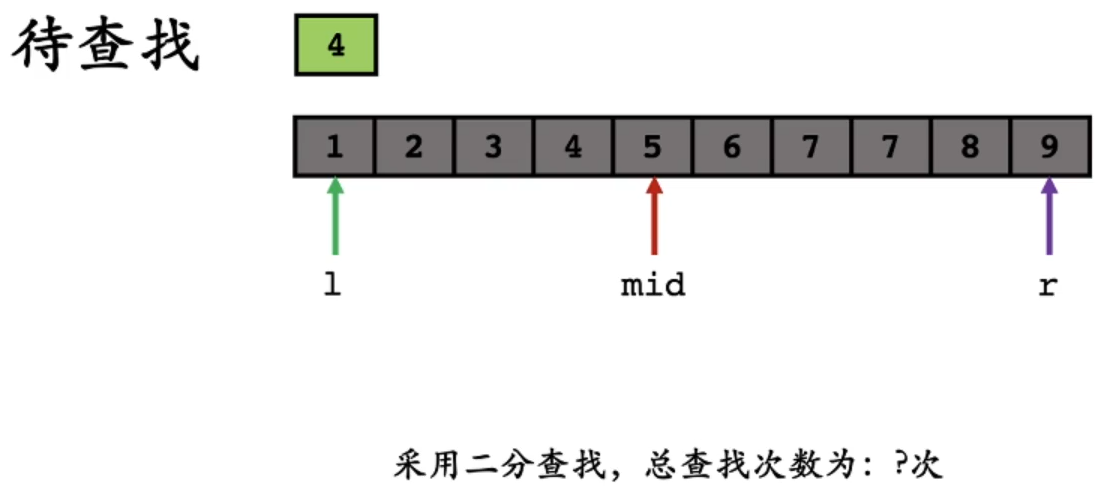
因为 a r r [ m i d ] > 4 arr[mid] > 4 arr[mid]>4,所以更新 r r r 的位置, r = m i d − 1 r=mid-1 r=mid−1:
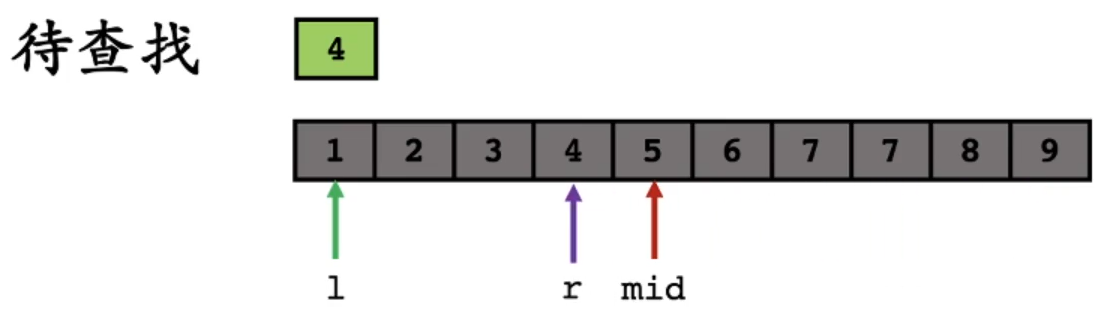
更新 m i d mid mid 的值:
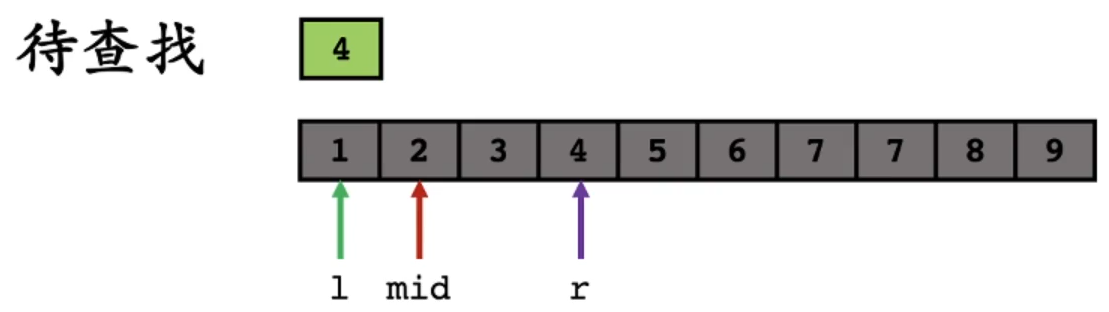
因为 a r r [ m i d ] < 4 arr[mid] < 4 arr[mid]<4,所以更新 l l l 的位置, l = m i d + 1 l=mid+1 l=mid+1:
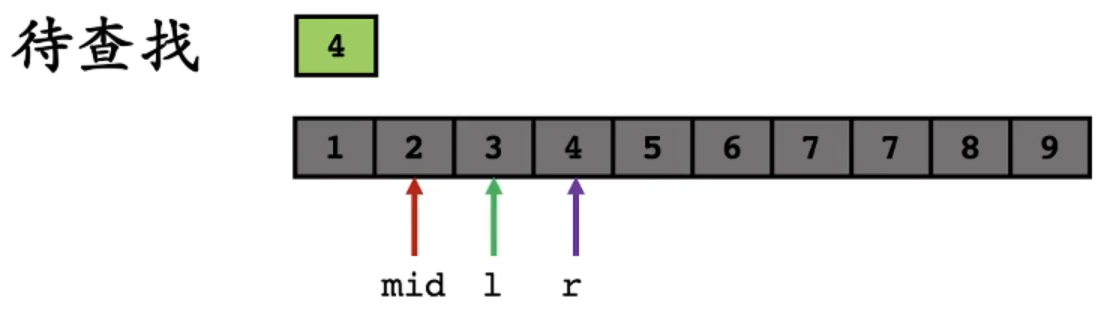
再次更新 m i d mid mid:
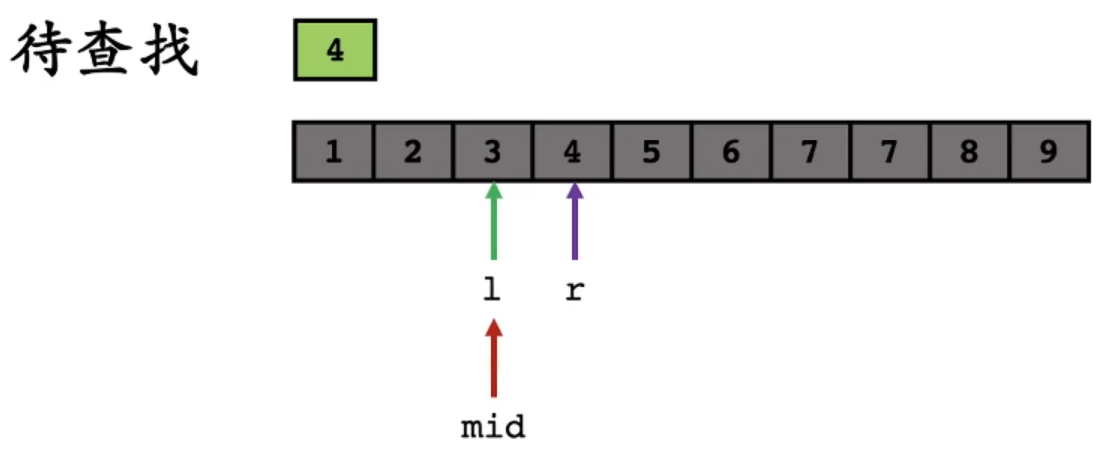
此时虽然 l l l 和 m i d mid mid 指向同一个位置,但 a r r [ m i d ] < 4 arr[mid] < 4 arr[mid]<4,所以此时 l = m i d + 1 l=mid+1 l=mid+1, l = = r l == r l==r,找到答案:
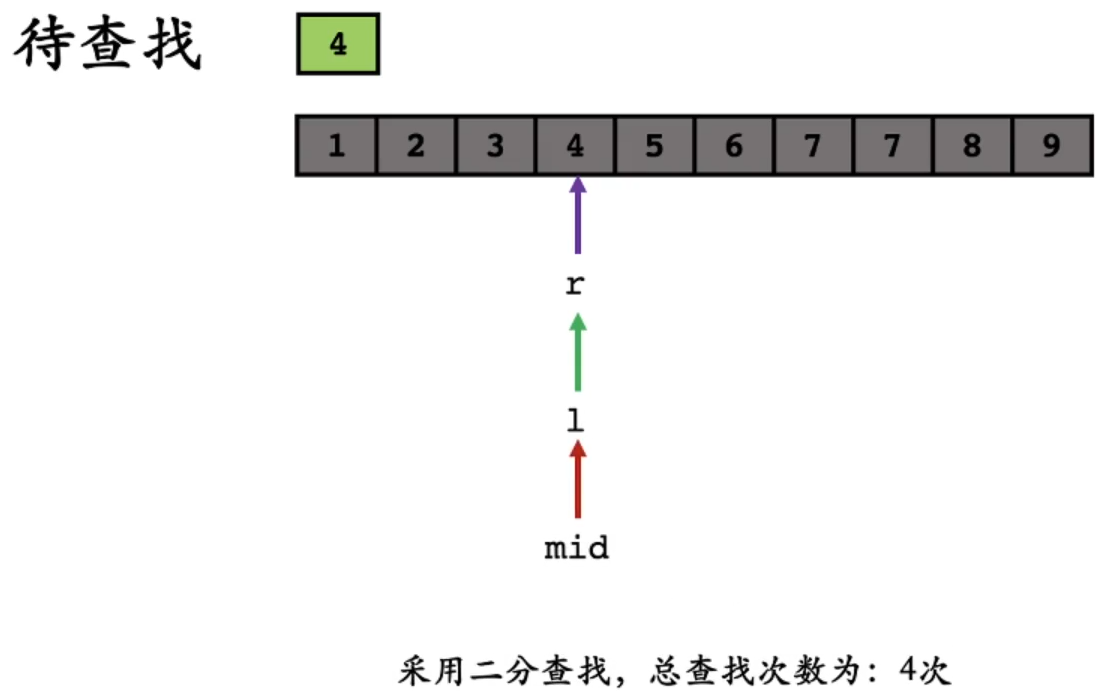
二分简单代码实现
public class BinarySearch { public static void main(String[] args) { int idx = binarySearch(new int[]{1, 2, 3, 4, 5, 6}, 5); System.out.println(idx); // sout: 4 } private static int binarySearch(int[] nums, int target) { int l = 0, r = nums.length - 1, mid; while (l <= r) { mid = (l + r) / 2; if (nums[mid] == target) { return mid; } else if (nums[mid] > target) { r = mid - 1; } else { l = mid + 1; } } return -1; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
二分查找—泛型情况
二分的两种变形
- 第一种:假如我们的 t a r g e t = 1 target=1 target=1,我们需要找到最后一个小于等于 1 1 1 的值,和第一个大于等于 1 1 1 的值。
- 第二种:找到第一个出现的 1 1 1,和连续的最后一个出现的 1 1 1。
我们并不能找到 1 1 1 就算结束,需要满足题意的条件。
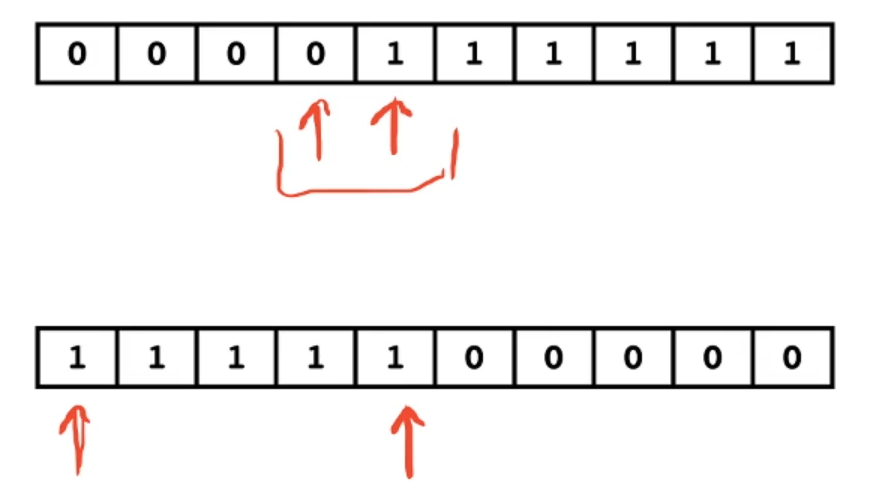
我们可以把这四种情况总结成一种情况:就是找第一个大于等于给定元素的写法,其它的泛型情况都可以用这一种写法推出来,只需要注意一下下标位置即可。
public class BinarySearch { public static void main(String[] args) { int idx = binarySearch2(new int[]{0, 0, 0, 2, 2, 2}, 1); System.out.println(idx); // sout: 3 } // 查找第一个大于等于给定值的元素位置 private static int binarySearch2(int[] nums, int target) { int l = 0, r = nums.length - 1, mid; while (l <= r) { mid = (l + r) / 2; if (nums[mid] == target) { r = mid - 1; // r指向的值永远不可能是target } else if (nums[mid] > target) { r = mid - 1; } else { l = mid + 1; // 如果找不到,l指向的值就是数组里面第一个大于等于target的值 } } if (l == nums.length) return -1; // 防止越界 return l; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
类似题:LeetCode34. 在排序数组中查找元素的第一个和最后一个位置,在下面会写题解。
时间复杂度
每次二分后,数据都会减少一半: n , n 2 , n 4 , n 8 n,\ \frac{n}{2},\ \frac{n}{4},\ \frac{n}{8} n, 2n, 4n, 8n,所以通项公式为: n 2 k = 1 \frac{n}{2^k}=1 2kn=1
故: k = log 2 n k = \log_2n k=log2n
时间复杂度O ( log n ) O(\log n) O(logn)在面试中,如果面试官说,让你用 log n \log n logn 的算法改进一下这个题,只要说到 log n \log n logn 了,一定会用到二分思想(不是二分算法)。
二分中的数组和函数的关系
数组: a r r [ n ] = { 1 , 2 , 3 , 4 , 5 } arr[n] = \{1,2,3,4,5\} arr[n]={1,2,3,4,5}
函数: f x ( a ) = { 1 , 2 , 3 , 4.5 } fx(a)=\{1,2,3,4.5\} fx(a)={1,2,3,4.5},函数根据每次传递的参数不同,将每次的返回时展开后,也可以表示成类似数组的形式。
数组可以二分,那么函数也可以二分。
只要能把问题抽象成一个数学公式(模型)且具有单调性,就能在这个问题上做二分。
三次方根函数图像大概如下图:
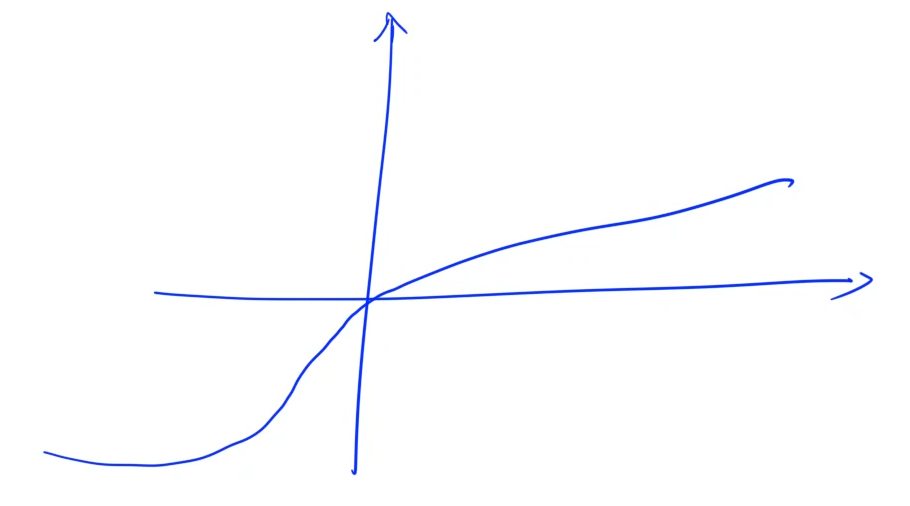
函数是有单调性的,有单调性一定可以二分,能二分不一定有单调性。
相关力扣题:LeetCode69. x 的平方根 ,在下面也会写题解。
LeetCode真题
经典面试题—简单二分应用
LeetCode35. 搜索插入位置
难度:
easy请必须使用时间复杂度为
O(log n)的算法。只要出现这句话,那么就需要使用二分查找去解决。
非常简单的二分,但我们之前写的:如果找不到这个元素会返回 − 1 -1 −1,但是本题要返回它将会被按顺序插入的位置,只需要改一下最后 r e t u r n return return 的值即可,那要怎么改呢?
在之前写的代码中,即使在数组中未找到该元素,那么 l l l 和 r r r 的值也都是有意义的, l l l 代表着数组中第一个大于目标值的元素, r r r 代表着第一个小于目标值的元素。
LeetCode题解:代码实现
LeetCode34. 在排序数组中查找元素的第一个和最后一个位置
难度:
mid你必须设计并实现时间复杂度为
O(log n)的算法解决此问题。经典的二分问题,寻找
左端点和右端点;这个题就是上面的二分查找—泛型情况。首先写一个二分方法,找到目标值的开始位置,再利用小trick,使得一个方法既可以返回目标值的起始位置 也可以返回结束位置。
具体看题解代码及注释。
LeetCode题解:代码实现
LeetCode69. x 的平方根
难度:
easy典型的函数二分。
注意: 不允许使用任何内置指数函数和算符
所以我们只能使用迭代的方式。
这个题转换为公式: f ( x ) = x f(x)=\sqrt{x} f(x)=x,对这个函数进行二分。
LeetCode题解:代码实现
LeetCode475. 供暖器
难度:
mid如果这道题我们想要用二分来做的话,需要先对这两个数组进行排序。
我们可以先遍历所有的房屋,看看哪一个供暖器离它的距离最近(前面找一个供暖器,后面找一个供暖器,看看哪一个供暖器离我最近)
供暖器...房屋..供暖器 ← 像这种情况选择右面的供暖器- 1
选择好之后,就可以认为加热半径就是这个距离。
那我们要怎么通过遍历来确定加热半径呢?
拿着房子的编号到加热器的编号中找假设两个数组中的元素如图中所示,遍历 h o u s e s [ ] houses[\ ] houses[ ] 数组时,每一个值去 h e a t e r s [ ] heaters[\ ] heaters[ ] 数组中找,找哪一个值离它最近,对于 1 1 1 和 2 2 2 来说,找到后面离它最近的值,也就是第一个大于等于它的值,也就是 3 3 3,再将它们相减就得到了加热半径。
那么对于 4 4 4 来说,它的前后都有供暖器,所以需要找到最后一个小于它的值,和第一个大于等于它的值,再进行比较,对应图中的供暖器 3 3 3 和 5 5 5 都可以,再进行相减即可得到加热半径。
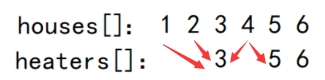
在进行寻找的过程中就可以使用二分查找。
最后在所有的加热半径中选择一个最大值就是这题的答案。
LeetCode题解:代码实现
经典面试题—复杂二分应用
LeetCode1. 两数之和
难度:
easy这道力扣的第一题也可以用二分来做,经典的 T w o S u m TwoSum TwoSum 问题。
因为要找出两数之和为 t a r g e t target target 的下标,我们换位思考,拿着 t a r g e t target target 去减数组中的数,然后在数组中寻找有没有这个差。
例如示例1,我们先拿着目标值 9 9 9 去减 2 2 2 等于 7 7 7,然后在数组中寻找有没有 7 7 7,如果没有再 9 − 7 = 2 9-7=2 9−7=2 去找数组中有没有 2 2 2,这样的寻找就可以使用二分查找。

如果我们要使用二分,前提必须保证它有序,但排完序后 每个数的下标就可能发生变化,无法正确返回原始下标,所以我们可以再开一个 i n d [ ] ind[\ ] ind[ ] 数组专门记录每一个元素的下标是多少,然后再根据原数组的大小进行排序 将新下标更新到 i n d [ ] ind[\ ] ind[ ] 数组中。
这道题可以用暴力 O ( N 2 ) O(N^2) O(N2)、哈希 O ( N ) O(N) O(N)、二分 O ( N log N ) O(N\log N) O(NlogN) 三个方法来做。
LeetCode题解:三种方法代码实现
LeetCode1658. 将 x 减到 0 的最小操作数
难度:
mid首先直接看这个题,是没法直接用二分来做的。
我们将这个问题转换一下,使用
前缀和+后缀和,再进行观察:原数组:1 1 4 2 3 前缀和:1 2 6 8 11 从左面删除1个..2个..3个..4个..5个 后缀和:11 10 9 5 3 从右面删除1个..2个..3个..4个..5个- 1
- 2
- 3
假设我们选择从左面删除 1 1 1 个元素,此时目标值为 5 5 5,那么 5 − 1 = 4 5-1=4 5−1=4,从后缀和数组中找有没有 4 4 4 ,如果找到了代表这是一种方案,可以这么删;从右面删同理。
如果前缀和 或 后缀和有目标值 5 5 5,同样也是一种方案。
这样 就将这个题转换为了 T w o S u m TwoSum TwoSum 问题。
LeetCode题解:代码实现
LeetCode81. 搜索旋转排序数组 II
难度:
mid一个数组 在某一个下标进行了旋转,例如,
[0,1,2,4,4,4,5,6,6,7]在下标5处经旋转后可能变为[4,5,6,6,7,0,1,2,4,4],此时我们可以根据下标5对旋转后的数组进行分隔,变为:[4,5,6,6,7, | 0,1,2,4,4],此时我们发现,分隔后的这两段值,每一段仍然是具有单调性的,如下图所示:
所以这道题还是可以用二分来做,我们只需要注意 m i d mid mid 是出现在前半段还是在后半段。
LeetCode题解:代码实现
LeetCode1011. 在 D 天内送达包裹的能力
难度:
mid首先我们发现这个题的数组是有序的,那么很容易就想到用二分来做。
我们先确定二分的区间 [ l , r ] [l,\ r] [l, r],那么最小值 l l l 就是数组中最大的值,最大值 r r r 就是数组中所有的重量的累加。
实现一个 c h e c k ( ) check() check() 函数,返回当前载重运送所需要的天数。
基于函数进行二分。
LeetCode题解:代码实现
LeetCode4. 寻找两个正序数组的中位数
难度:
hard我们由求中位数,转换成求两个合并的正序数组的第 k k k 个数。
合并之后找的是第 k k k 个数,那么将两个数组拆开,就是分别找数组中的第 k 2 \frac{k}{2} 2k 个数。
假设 a [ k 2 ] < b [ k 2 ] a[\frac{k}{2}] < b[\frac{k}{2}] a[2k]<b[2k],那么 a [ k 2 ] a[\frac{k}{2}] a[2k] 最多能排在第几位?
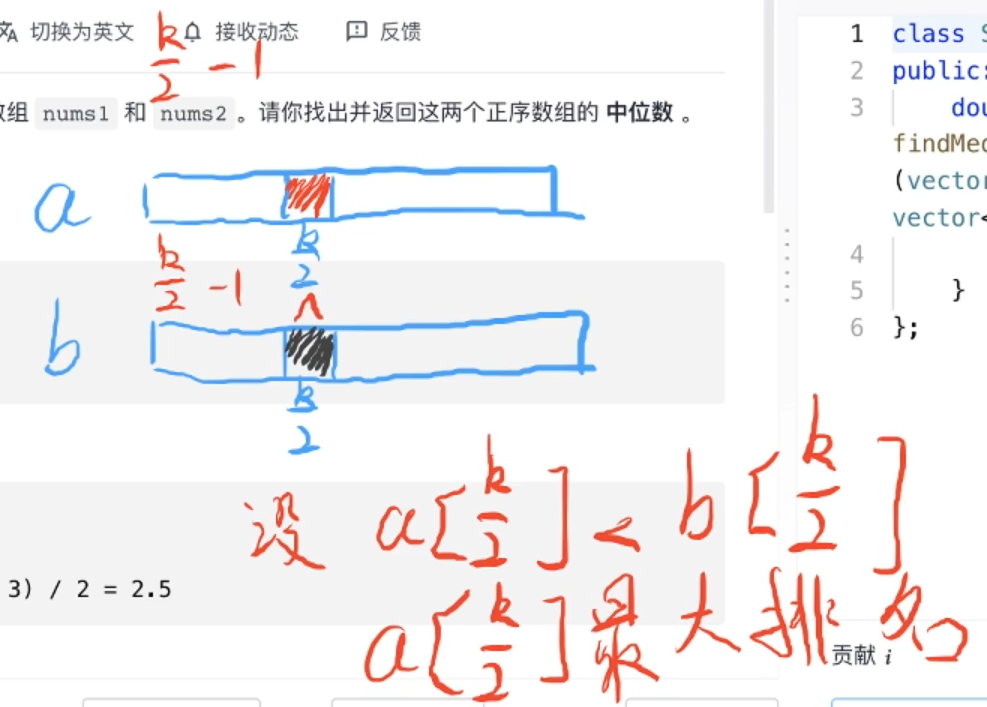
首先 a [ k 2 ] a[\frac{k}{2}] a[2k] 和 b [ k 2 ] b[\frac{k}{2}] b[2k] 前面值的个数都是 k 2 − 1 \frac{k}{2}-1 2k−1,合在一起就是 k − 2 k-2 k−2,所以 a [ k 2 ] a[\frac{k}{2}] a[2k] 的最大排名为 k − 1 k-1 k−1(最好的情况下)。
所以黄色部分就更不可能是第 k k k 个元素了:
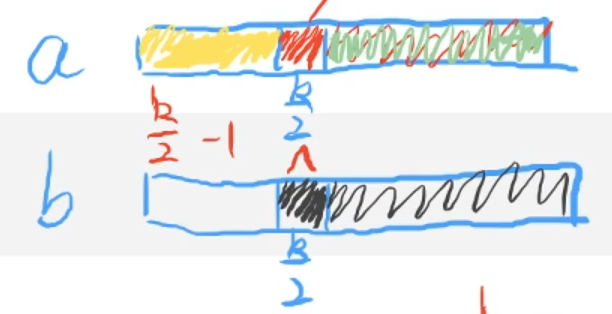
所以我们可以把黄色部分和红色部分砍掉,因为它们永远到不了第 k k k 位,从而减少了区间范围。
如果 a [ k 2 ] < b [ k 2 ] a[\frac{k}{2}] < b[\frac{k}{2}] a[2k]<b[2k],那么就减少 a [ ] a[\ ] a[ ] 的部分,如果 a [ k 2 ] > b [ k 2 ] a[\frac{k}{2}] > b[\frac{k}{2}] a[2k]>b[2k],那么就减少 b [ ] b[\ ] b[ ] 的部分,哪边小就删哪边,不断减少范围。
LeetCode题解:代码实现
LeetCode300. 最长递增子序列
难度:
mid这道题是一道经典的DP问题,但也可以用
贪心+二分来做,是时间复杂度最优的解法。- 贪心思想:保证递增的子序列的最后一个数值尽量小,这样维护的一个子序列最终才会更长。
首先我们需要创建一个数组,记录我们的递增子序列。
逐一遍历原数组,并更新我们的递增子序列数组,如示例1:
10,9,2,5,3,7,101,18 遍历原数组 递增子序列数组中的值 10: 10 (直接放入10) 9: 9 (9比10小 所以直接替换10) 2: 2 (2比9小 所以直接替换9) 5: 2,5 (5比2大 所以可以放在2的后面) 3: 2,3 (3比5小 所以直接替换5) 7: 2,3,7 (7比3大 所以可以放在2,3的后面) 101: 2,3,7,101 (101比7大 所以可以放在2,3,7的后面) 18: 2,3,7,18 (8比101小 所以直接替换101 因为是贪心的思想 即使达到最大长度也会替换)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
我们发现这道题用这种方式来思考,它就是一道 01 01 01 模型的题,找 01 01 01 模型中第一个 1 1 1 的位置,这个位置就是它的长度,我们不断更新这个长度,就可以得到一个最长的递增子序列。
LeetCode题解:两种方法代码实现 (dp、贪心 + 二分)
总结
二分其实是一个很大的概念,一般想到搜索的话,无非就是dfs、bfs和二分,其余的搜索基本都是这三种的变形。
而对于二分的模板来说,在这篇文章我大部分使用的都是
while (l <= r),而跟y总学习二分的时候使用的都是while (l < r),这两种模板看个人喜好,哪个好理解一点就用哪个。二分一定要灵活的使用,不要死记模板,当然简单题一个模板就可以AC了,遇到复杂一点的题,适当变通一下 if else 的条件,也是可以做出来的。
-
相关阅读:
面试官:bind、call、apply 区别?如何实现一个bind?
【重温设计模式】迭代器模式及其Java示例
PTA 7-151 最大公约数
为什么反射慢?
【SpringCloud】02-服务注册与发现-Zookeeper
哪些企业需要数字化转型?
jsp 的div表格示例
Linux自动化运维工具ansible详解
python-(6-3-2)爬虫---requests入门(基于post请求)
(路径、文件)常用命令
- 原文地址:https://blog.csdn.net/weixin_53407527/article/details/126575492
