快速幂实战

快速幂用来高效计算高次方，正常计算时间复杂度为O(n)，使用快速幂可以做到O(log₂n)

斐波那契数列概念

F(0)=0，F(1)=1

当n>1时，且n为正整数时，F(n)=F(n-1)+F(n-2)

三种实现方式

1. 递归，时间复杂度O(2^n)
2. 动态规划，时间复杂度O(n)
3. 矩阵快速幂，时间复杂度O(log₂n)

一、递归

递归的思路，从上往下算。

public static int fib(int n) {
    if (n < 2) {
        return n;
    } else {
        return fib(n - 1) + fib(n - 2);
    }
}
1
2
3
4
5
6
7

二、动态规划

动态规划的思路，从下往上算。

通过递归的结果，查看前十项规律。

0 1 1 2 3 5 8 13 21 34

可知每一项都是前两项之和，这三个元素可以通过一个数组存储计算。

public static int fibDP(int n) {
    if (n < 2) {
        return n;
    } else {
        int[] arr = new int[3];
        arr[1] = 1;
        arr[2] = 1;
        for (int i = 2; i < n; i++) {
            int res = arr[2] + arr[1];
            arr[0] = arr[1];
            arr[1] = arr[2];
            arr[2] = res;
        }
        return arr[2];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

三、矩阵快速幂

3.1 快速幂

正常的求高次方a^n，时间复杂度是O(n)

比如

public static int power(int a, int n) {
    int res = 1;
    for (int i = 0; i < n; i++) {
        res = res * a;
    }
    return res;
}
1
2
3
4
5
6
7

但是这个方式是可以优化的，也就是所谓的快速幂

快速幂的思路，就是将之前遍历相乘n次，降低到只需遍历相乘

举例来说，对于a^11，推导过程如下
$$a^{11}=a^{1\ast 2^3+0\ast 2^2+1\ast 2^1+1{\ast }^0}=a^{2^3}\ast a^{2^1}\ast a^{2^0}=a^8\ast a^2\ast a^1$$
通过第一个等号后面的内容的乘方，可知指数的系数恰好是十进制11的二进制1011，最后的结果就是二进制位为0时，不计算。

那么计算a^11只需要遍历3次。

再次验证a^12，推导过程如下
$$a^{12}=a^{1\ast 2^3+1\ast 2^2+0\ast 2^1+0\ast 2^0}=a^{2^3}\ast a^{2^2}=a^8\ast a^4$$
那么计算a^12只需要遍历2次。

求多个相同因数的积的运算叫做乘方，乘方的结果叫做幂，相同因数就是底数，而因数的个数是指数。

接下来是如何求二进制，这个简单，放个例子。

public static String DecToBin(int dec) {
    StringBuilder sb = new StringBuilder();
    while (dec > 0) {
        // 依次取余求二进制低位
        if (dec % 2 == 1) {
            sb.insert(0, 1);
        } else {
            sb.insert(0, 0);
        }
        dec = dec / 2;
    }
    return sb.toString();
}
1
2
3
4
5
6
7
8
9
10
11
12
13

结合上步的推导结果，如果二进制位为0时，不计算，由此实现简单的快速幂。

public static int fastPower(int a, int n) {
    int res = 1;
    while (n > 0) {
        //n&1==1表示n为奇数
        //n%2==1表示n为奇数，两者相等
        if ((n & 1) == 1) {
            res = res * a;
        }
        a = a * a;
        //n/2与n>>1含义一样
        n = n >> 1;
    }
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

快速幂算法的核心思想就是通过二进制右移计算，依次求二进制的低位，如果低位是1，就乘上底数，同时相应的底数每次自身都会做平方运算，这样不仅能把非常大的指数给不断变小，所需要执行的循环次数也变小，并且计算结果一样。

3.2 优化解法

知道了快速幂的解法。根据斐波那契数列的规定，构造递推关系
[ 1 1 1 0 ] [ F ( n ) F ( n − 1 ) ] = [ F ( n ) + F ( n − 1 ) F ( n ) ] = [ F ( n + 1 ) F ( n ) ]

== [11​10​][F(n)F(n−1)​]=[F(n)+F(n−1)F(n)​]=[F(n+1)F(n)​]

= [ 1 1 1 0 ] n [ F ( 1 ) F ( 0 ) ] =

^n =[11​10​]n[F(1)F(0)​]

= [ 1 1 1 0 ] n [ 1 0 ] =

^{n} =[11​10​]n[10​]

经如上推导，求斐波拉契数列的关键一步，就是求出n次方矩阵M来，最终的F(n)=M[1][0];

代码实现

/**
 * 基于矩阵快速幂解斐波那契数列
 *
 * @param n
 * @return
 */
public static int fibFastPower(int n) {
    if (n < 2) {
        return n;
    } else {
        int[][] a = {{1, 1}, {1, 0}};
        a = rectFastPower(a, n);
        return a[1][0];
    }
}

/**
 * 矩阵快速幂
 * 借鉴快速幂思想，将a数组看做一个普通数
 *
 * @param a
 * @param n
 * @return
 */
public static int[][] rectFastPower(int a[][], int n) {
    //res应取1，左斜乘积-右斜乘积即为值
    int[][] res = {{1, 0}, {0, 1}};
    while (n > 0) {
        if ((n & 1) == 1) {
            res = rectMultiply(res, a);
        }
        a = rectMultiply(a, a);
        n = n >> 1;
    }
    return res;
}

/**
 * 矩阵乘积
 *
 * @param a
 * @param b
 * @return
 */
public static int[][] rectMultiply(int[][] a, int[][] b) {
    int[][] res = new int[2][2];
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            //该关系式可以通过推导得出
            res[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];
        }
    }
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

代码中的关系式推导过程如下

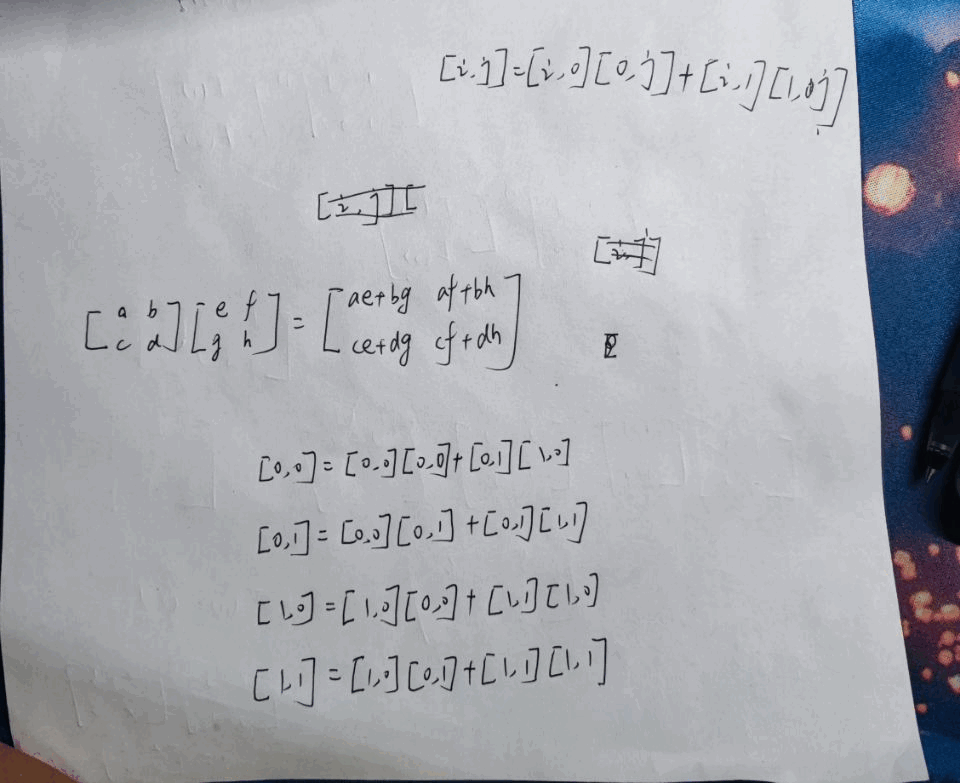
四、参考致谢

在线LaTeX公式编辑器-编辑器

快速幂_百度百科

矩阵快速幂 | 幻悠尘的小窝

快速幂详解（超详细！！！）_m725kk的博客-CSDN博客_kuaisumi

斐波那契数列 - 斐波那契数列 - 力扣（LeetCode）