-
奇虎360Java笔试题
1题
执行以下程序后的输出结果是()
public class Test {
public static void main(String[] args) {
StringBuffer a = new StringBuffer(“A”);
StringBuffer b = new StringBuffer(“B”);
operator(a, b);
System.out.println(a + “,” + b);
}
public static void operator(StringBuffer x, StringBuffer y) {
x.append(y); y = x;
}
}
答案:AB,B
解析:a,b是对象的引用,指向堆内存,将a,b两个引用传给x,y,执行x.append(y),改变了x引用指向的堆内存的存储内容,变为AB, y = x,表示引用y,指向引用x指向的存储区域,没有改变引用b,指向的存储空间的内容。一句话解决:string是值传递,stringbuffer是引用传递。。所以就这样了。
2题
结构型模式中最体现扩展性的几种模式是()
答案:装饰模式
解析:A 装饰模式
定义:动态给一个对象添加一些额外的职责,就象在墙上刷油漆.使用Decorator模式相比用生成子类方式达到功能的扩充显得更为灵活。
设计初衷:通常可以使用继承来实现功能的拓展,如果这些需要拓展的功能的种类很繁多,那么势必生成很多子类,增加系统的复杂性,同时,使用继承实现功能拓展,我们必须可预见这些拓展功能,这些功能是编译时就确定了,是静态的。装饰模式的作用就是为了:
1.扩展功能
2.不用继承
从这点来说可以算“最能体现”扩展性吧。
3题
在Linux中,对file.sh文件执行#chmod 645 file.sh中,该文件的权限是()
答案:-rw-r–r-x
解析:Linux下权限对应的数字为:
r =4, w =2, x =1
所以,6就是rw-
4就是r–
5就是r-x
所以,选D
4题
TCP建立连接的过程采用三次握手,已知第三次握手报文的发送序列号为1000,确认序列号为2000,请问第二次握手报文的发送序列号和确认序列号分别为
答案:1999,1000
解析:发送序列是自己发送报文的序列号,当前发送序列号是上一次发送序列号+1
确认序列号是从对方接收到的发送序列号+1
第三次握手发送的序列号是1000,那说明第一次握手发送的序列号是999,注意:这里是握手
,因此,第二次握手的确认序列号是1000,即确认序列号是从对方接收到的发送序列号+1。
第三次握手发送的确认号是2000,说明第二次握手的发送序列号是1999。
所以,选B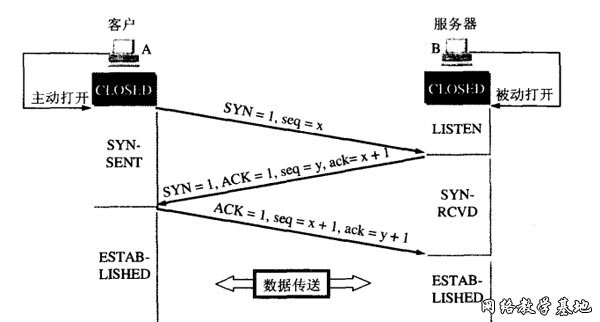
5题
下列TCP连接建立过程描述正确的是:
答案:当客户端处于ESTABLISHED状态时,服务端可能仍然处于SYN_RCVD状态
解析:此题主要考察TCP三次握手,四次挥手的状态变化,对着图看吧,加深印象。
三次握手如下:
6题
属于网络112.10.200.0/21的地址是()
答案:112.10.206.0
解析:前21位为网络地址,后12位为主机地址。
110 对应前8位,10对应第二个8位,因此200对应第3个8位
又200的二进制表示为1100 1000
前面已经有了16位,因此11001 是属于网络地址的。000是属于主机地址 那么,最大的地址为
【110(十进制)】【10(十进制)】【11001 111】【 11111111】转换为十进制为110.10.207.255
故网络的地址范围为
110.10.200.0~110.10.207.255
故A为正确答案
7题
以下java程序代码,执行后的结果是()
java.util.HashMap map=new java.util.HashMap();
map.put(“name”,null);
map.put(“name”,”Jack”);
System.out.println(map.size());
答案:1
解析:HashMap可以插入null的key或value,插入的时候,检查是否已经存在相同的key,如果不存在,则直接插入,如果存在,则用新的value替换旧的value,在本题中,第一条put语句,会将key/value对插入HashMap,而第二条put,因为已经存在一个key为name的项,所以会用新的value替换旧的vaue,因此,两条put之后,HashMap中只有一个key/value键值对。那就是(name,jack)。所以,size为1.
8题
以下java程序代码,执行后的结果是()
public class Test {
public static void main(String[] args) {
Object o = new Object() {
public boolean equals(Object obj) {
return true;
}
};
System.out.println(o.equals(“Fred”));
}
}
答案:true
解析:1.建立了一个匿名内部类,并重写了Object的equals方法。
2.通过o调用了equals方法,方法返回true。
9题
代码片段:
byte b1=1,b2=2,b3,b6;
final byte b4=4,b5=6;
b6=b4+b5;
b3=(b1+b2);
System.out.println(b3+b6);
关于上面代码片段叙述正确的是()
答案:语句:b3=b1+b2编译出错
解析:表达式的数据类型自动提升, 关于类型的自动提升,注意下面的规则。
①所有的byte,short,char型的值将被提升为int型;
②如果有一个操作数是long型,计算结果是long型;
③如果有一个操作数是float型,计算结果是float型;
④如果有一个操作数是double型,计算结果是double型;
而声明为final的变量会被JVM优化,第6行相当于 b6 = 10
若有不对,请指正
10题
下面代码运行结果是()
public class Test{
public int add(int a,int b){
try {
return a+b;
}
catch (Exception e) {
System.out.println(“catch语句块”);
}
finally{
System.out.println(“finally语句块”);
}
return 0;
}
public static void main(String argv[]){
Test test =new Test();
System.out.println(“和是:”+test.add(9, 34));
}
}
答案:finally语句块,和是:43
解析: 程序先执行try块中return之前(包括return语句中的表达式运算)的代码; 再执行finally块,最后执行try块中的return; 而 finally块之后的return语句,因为程序在try块中已经return了,所以不再执行。
11题
以下情况下不一定出现TCP分节RST的情况是:
答案:服务器主机崩溃后重启
解析:四种情况会发送RST包:
1、端口未打开
2、请求超时
3、提前关闭
4、在一个已关闭的socket上收到数据
12题
一个数据库中现有A,B,C,D,E,F六个语句但目前这个数据库是不协调的,必须删除某些语句才能恢复数据库的协调性。已知:(1)如果保留语句A,那么必须保留语句B和C。(2)如果保留语句E,则必须同时删除语句D和语句C。(3)只有保留语句E,才能保留语句F。(4)语句A是重要的信息,不能删除以上各项如果为真,则以下哪项一定为真?
答案:同时删除语句E和语句F
解析:根据(4),A必须有;
再根据(1),B,C必须有,此时一定有ABC
根据(2),因为有C,所以一定没有E
根据(3),因为没有E,所以一定没有F
综上,ABC一定有,EF一定没有,D不确定
13题
下列关于静态工厂和工厂方法表述错误的是:()
答案:二者都满足开闭原则:静态工厂以if else方式创建对象,增加需求的时候会修改源代码
解析:选D,开闭原则:对扩展开放,对修改封闭。静态工厂增加需要是修改源代码,对修改不封闭,不符合开闭原则。
14题
设有一个用数组Q[1…m]表示的环形队列,约定f为当前队头元素在数组中的位置,r为队尾元素的后一位置(按顺时针方向),若队列非空,则计算队列中元素个数的公式应为()
答案:(m+r-f)mod m
解析:(1)当尾大于头长度为 尾 - 头当尾小于头 例如尾巴在2号位置,而头在4号位置。表的长度为4 1 2,而这段长度为 总长度 - (尾 -头 ) = 总长度 - ( 尾 -头 ) 而 ( 尾 -头 ) < 0所以 得到 总长度+ ( 尾 -头 ) 。
因此合并两个表达式 得到 (总长度+ ( 尾 -头 ))%总长度 ,% 防止(1)情况发生溢出。
1
4 2
3
15题
以下程序是用辗转相除法来计算两个非负数之间的最大公约数:
long long gcd(long long x,long long y){
if(y0)
return x;
else return gcd(y,x%y);
}
我们假设x,y中最大的那个数的长度为n,基本基本运算时间复杂度是O(1),那么该程序的时间复杂度为()
答案:O(logn)
解析:快速的思路是排除法,不是与固定几个值计算,所以不是O(1)的,当然也不会把每个数都遍历个遍来确定,不是O(n)和O(n^2)的,于是选择A。
当然如果感兴趣的话,可以做一个实验:在10000以内两两辗转相除法,运算次数最多的是哪两个数呢?
6765和 4181
如果把上界再缩小或扩大,你会发现,出现的数都是斐波那契数列中的数,都是相邻的两项。
因为斐波那契数列相邻两项在做gcd的时候,每次mod只相当于做了一次a-b,退化成更相减损术了,而没有起到mod的加速效果。
而斐波那契数列有通项公式,第n项的值是与某两个无理数的n次相关的。所以,是logn了
(当然这个证明还是很不科学的)
16题
计算斐波那契数列第n项的函数定义如下:
int fib(int n){
if(n0)
return 1;
else if(n==1)
return 2;
else
return fib(n-1)+fib(n-2);
}
若执行函数调用表达式fib(10),函数fib被调用的次数是:
答案:177
解析:f(10)=f(9)+f(8)+1
= 2f(8)+f(7)+2
=3f(7)+2f(6)+4
=5f(6)+3f(5)+7
…
=55f(1)+34f(0)+88
55+34+88=177
17题
设图G的相邻矩阵如下图:则G的顶点数和边数分别为:
0 1 1 1 1
1 0 1 0 0
1 1 0 1 1
1 0 1 0 1
1 0 1 1 0
答案:5,8
解析:笨方法:把图按照相邻矩阵画出来;
简单方法:只计算主对角线的上三角或下三角有多少个 1 即可。矩阵为5*5,则有五个顶点;关于主对角线对称,则为无向图;无向图中,边数目等于上/下三角矩阵中的非零元素数目。 -
相关阅读:
PWN环境搭建
Python 自动化教程(2) : Excel自动化:使用pandas库
Word | 添加图题/图注、插入题注、设置插入题注快捷键...
14条最佳JavaScript代码编写技巧
电力调度自动化系统,如何减少配电安全隐患?
[附源码]Python计算机毕业设计Django农产品销售网站
最佳生物信息工作环境(2023年11月更新版)
网络架构学习1
树状数组笔记
ApiFox添加全局参数
- 原文地址:https://blog.csdn.net/m0_67401417/article/details/126565648